Delta Mush in Unreal Engine with the Deformer Graph
Introduction
Analysis of the asset:
Content/ExampleContent/AnimationDeformer/AnimBlueprints/DG_DeltaMushDeformerDemo.uasset
found in the sample scene provided in the content examples (see Epic Games market place). This asset offers an advanced use case of the deformer graph plugin in UE (which is the tech allowing to implement ML deformation by the way)
Algorithm overview
Let's recall how delta mush works:
Precompute:
- At each vertex, compute tangent space, i.e. a local frame coordinate which origin is the vertex and is aligned with the vertex' normal and tangent.
Per vertex TBN (tangent, binormal, normal) can be obtained with UVs, or face center.
- Smooth mesh in rest pose (e.g. Laplacian smoothing)
- Compute and store deltas vectors that encodes the difference between the original rest position and the smooth rest position. The per vertex deltas are represented in tangent space (the UE sample does it at runtime so this is an area for improvement)
Runtime:
- Smooth deformed mesh (deformation can be anything, skinning, lattice etc.)
- compute tangent space
- Apply delta vectors to restore details.
Implementation
Setup Graph
Precomputation is done in the setup graph 
:
A mesh is simply smoothed out in rest pose (uniform Laplacian smoothing with 8 hard coded iterations)
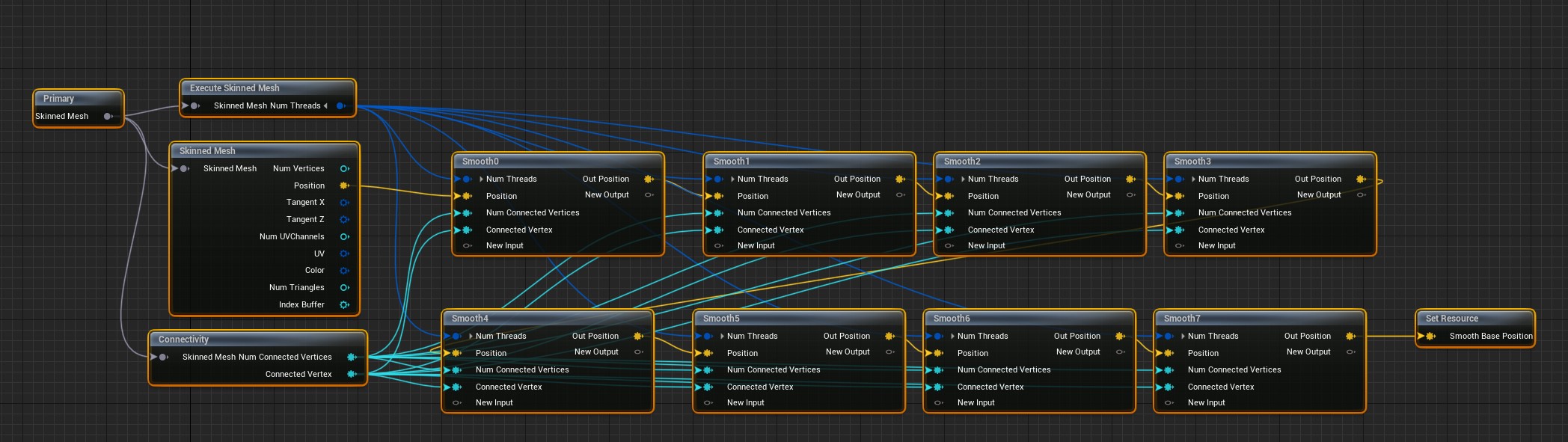
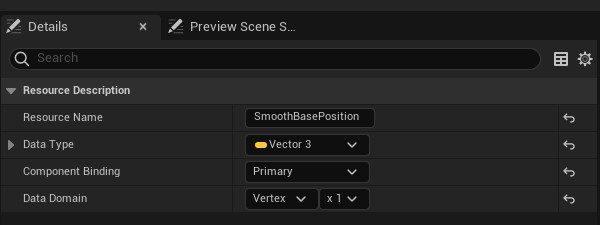
The result is written in a resource buffer SmoothBasePosition
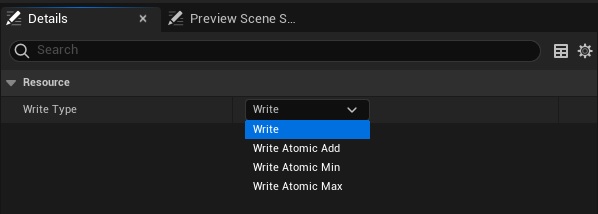
The setter of SmoothBasePosition is not configured to use any particular mutex and write type is simply set to "Write"
Kernel code for one iteration of smoothing:
if (Index >= ReadNumThreads().x) return;
float3 Position = ReadPosition(Index);
float3 PositionSum = Position;
uint MaxConnected = ReadNumConnectedVertices(Index);
uint NumConnected = 0;
for (; NumConnected < MaxConnected; NumConnected++)
{
uint ConnectedIndex = ReadConnectedVertex(Index, NumConnected);
if (ConnectedIndex == 0xFFFFFFFF)
{
break;
}
PositionSum += ReadPosition(ConnectedIndex);
}
float3 SmoothPosition = PositionSum / (float)(NumConnected + 1);
WriteOutPosition(Index, SmoothPosition);
Update graph
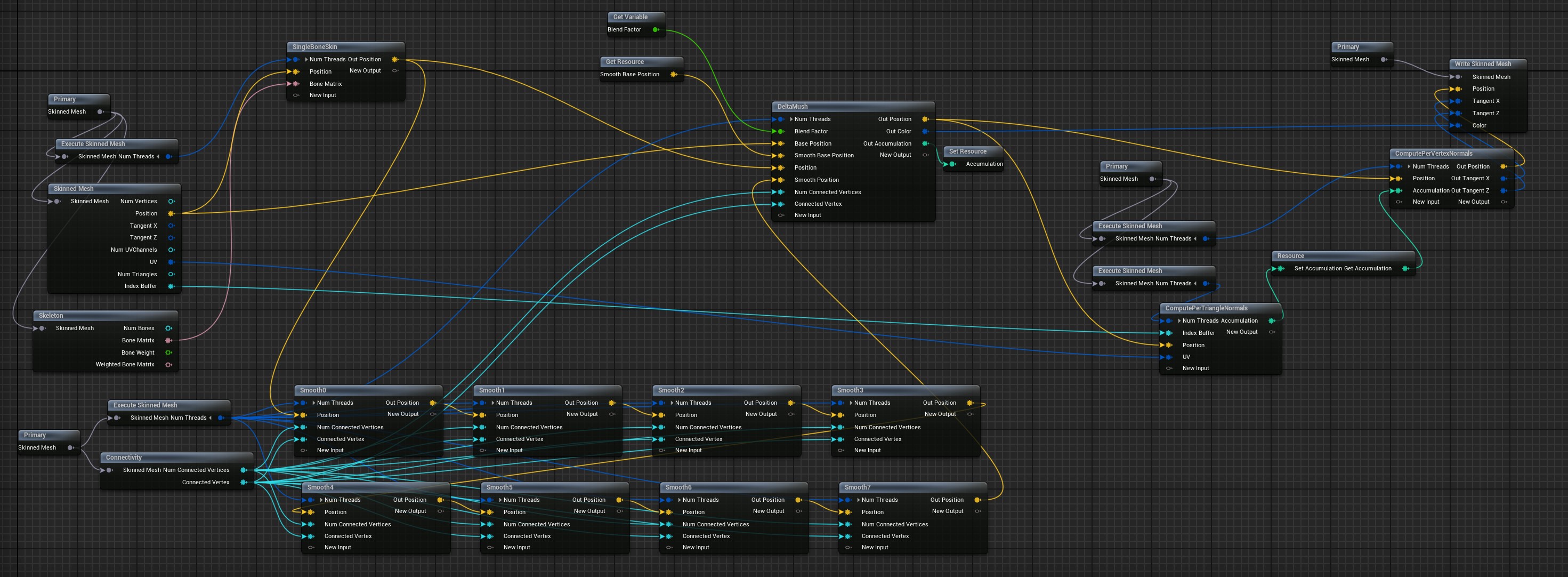
Kernel for rigid skinning (only max influence taken into account at each vertex)
// Kernel name: SingleBoneSkin if (Index >= ReadNumThreads().x) return; float3 LocalPosition = ReadPosition(Index); // Unreal sorts bone influence from max to min: float3x4 BoneMatrix = ReadBoneMatrix(Index, 0); float3 SkinnedPosition = mul(BoneMatrix, float4(LocalPosition, 1)); WriteOutPosition(Index, SkinnedPosition);
Delta Mush deformation core kernel code:
/*
Kernel name: DeltaMush
Execution domain: Vertex
Group size: 64 1 1
*/
// Accumulation resource should be NumVertices * 8.
#define ACCUMULATION_BUFFER_NUM_INTS 8
// For a vertex P0 compute a local frame purely based
// on outward triangle edges.
float3x3 GetVertexMatrix(float3 P0, float3 P1, float3 P2)
{
float3 Edge1 = normalize(P1 - P0);
float3 Edge2 = normalize(P2 - P0);
float3 Normal = normalize(cross(Edge1, Edge2));
float3 Binormal = normalize(cross(Edge1, Normal));
return float3x3(Edge1, // [0]
Normal, // [1]
Binormal // [2]
);
}
KERNEL
{
if (Index >= ReadNumThreads().x)
return;
float BlendFactor = ReadBlendFactor();
float3 BasePosition = ReadBasePosition(Index); // Rest Pose
float3 SmoothBasePosition = ReadSmoothBasePosition(Index); // Rest Pose smoothed 8 times
float3 SmoothPosition = ReadSmoothPosition(Index); // Rigid skinning smoothed 8 times
float3 Position = ReadPosition(Index); // Rigid skinning
float3 AdjustedPosition = Position; // Deformed mesh / Output
/*
We pick two edges in the list of adjacent vertices:
ConnectedIndex2
*
/
/ (Edge2)
/
Index *----------* ConnectedIndex1
(Edge1)
*/
uint ConnectedIndex1 = ReadConnectedVertex(Index, 0);
uint ConnectedIndex2 = ReadConnectedVertex(Index, 1);
if (ConnectedIndex1 != 0xFFFFFFFF &&
ConnectedIndex1 != 0xFFFFFFFF)
{
// Ideally we would want to precompute this part (the Delta)
// in the SetupGraph
float3x3 BaseVertexMatrix = GetVertexMatrix(SmoothBasePosition,
ReadSmoothBasePosition(ConnectedIndex1),
ReadSmoothBasePosition(ConnectedIndex2));
float3 GlobalDelta = BasePosition - SmoothBasePosition;
// BaseVertexMatrix is a rowMajor representation so
// matrix multiplication is from left to right:
// vec * Matrix
//
// However we want to transform by the inverse
// BaseVertexMatrix^-1
// Well, BaseVertexMatrix is an orthogonal matrix by construction
// So we only need to transpose it.
// And actually, multiplying from right to left is the same as doing:
// vec * BaseVertexMatrix^T
// Which is why we get the local delta with:
float3 Delta = mul(BaseVertexMatrix, GlobalDelta);
// This has to be done in the runtime though:
// We compute the local frame of the animated and smoothed position:
float3x3 VertexMatrix = GetVertexMatrix(SmoothPosition,
ReadSmoothPosition(ConnectedIndex1),
ReadSmoothPosition(ConnectedIndex2));
// Transform back the local Delta to global coordinates and apply it to
// the current position:
float3 DeltaMushPosition = mul(Delta, VertexMatrix) + SmoothPosition;
AdjustedPosition = lerp(Position, DeltaMushPosition, BlendFactor);
}
float3 DebugDiffColor = abs(Position - AdjustedPosition) / 1;
WriteOutPosition(Index, AdjustedPosition);
float4 AColor = float4(DebugDiffColor, length(DebugDiffColor));
WriteOutColor( Index, saturate(AColor) );
// Clear the accumulation buffer before use.
for (int Acc = 0; Acc < ACCUMULATION_BUFFER_NUM_INTS; ++Acc)
WriteOutAccumulation(Index * ACCUMULATION_BUFFER_NUM_INTS + Acc, 0);
}
Compute Normals and tangents
After deformation we need to compute normal from scratch, this is done by computing the normal at each triangle and summing this result to each vertex that belongs to the triangle. When summing to the corresponding vertex, for better accuracy, each normal is weighted by the angle between the outward edges of that vertex. To understand the code it's best to have knowledge on tangent space computation (OpenGl tutorial, small summary) . Polygon Mesh Processing also covers the logic behind weighting normal by the corner angle of a triangle.
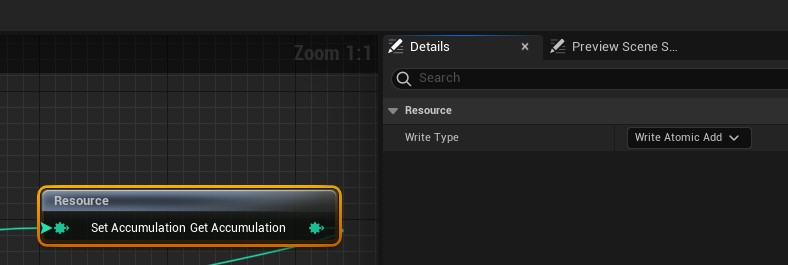
To accumulate the resulting normal and tangents we set the resource buffer Accumulation "write type" to "Write Atomic Add":
Portion of the graph to re-compute tangents (I disconnected "NumThreads" pins for visibility):
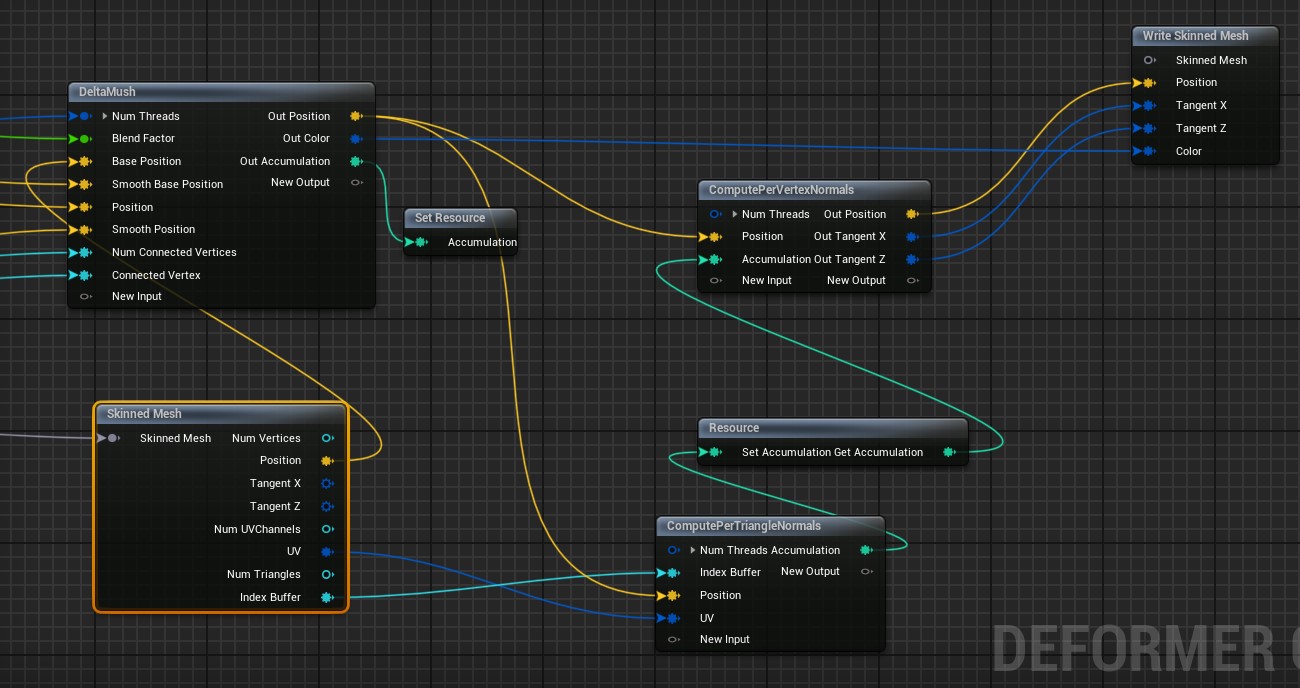
Kernel ComputePerTriangleNormals
/*
Execution domain: triangle
*/
// Accumulation resource should be NumVertices * 8.
#define ACCUMULATION_BUFFER_NUM_INTS 8
#define TANGENT_RANGE 0x7fff
struct FVertexData
{
uint VertexIndex;
float3 Position;
float2 UV;
/*
If we name:
- the current vertex 'a'.
- the current triangle vertices 'a', 'b' and 'c'
Then:
Angle = AngleBetween( Vec(b-a), Vec(c-a) )
*/
float Angle;
};
struct FTriangleTangentData
{
float3 TangentX; // Tangent T
float3 TangentZ; // Normal N
float Orientation; // Binormal orientation (1: B = cross(T, N); -1: cross(N, T))
};
FTriangleTangentData CalculateTriangleTangentData(in FVertexData Corners[3])
{
FTriangleTangentData Out;
float3 EdgeA = Corners[1].Position - Corners[0].Position;
float3 EdgeB = Corners[2].Position - Corners[0].Position;
float3 TriangleNormal = cross(EdgeB, EdgeA);
float3 TangentZ = normalize(TriangleNormal);
float2 UVEdgeA = Corners[1].UV - Corners[0].UV;
float2 UVEdgeB = Corners[2].UV - Corners[0].UV;
float CP = UVEdgeA.y * UVEdgeB.x - UVEdgeA.x * UVEdgeB.y;
float3 UnnormalizedTangentX = (EdgeB * UVEdgeA.y - EdgeA * UVEdgeB.y) / CP;
if (abs(CP) < 0.000001f)
{
// Bad UV assignment? Select some other vector that is orthogonal to TangentZ.
float3 Other = (abs(normalize(TangentZ).z) < 0.5f) ? float3(0, 0, 1) : float3(1, 0, 0);
UnnormalizedTangentX = cross(Other, TangentZ);
}
Out.TangentX = normalize(UnnormalizedTangentX);
Out.TangentZ = TangentZ;
Out.Orientation = (CP > 0) ? 1 : -1;
return Out;
}
KERNEL
{
if (Index > ReadNumThreads().x)
return;
uint TriangleIndex = Index;
// Gather per vertex information for each triangle corner.
uint CornerId;
FVertexData Corners[3];
UNROLL for (CornerId = 0; CornerId < 3; ++CornerId)
{
uint VertexIndex = ReadIndexBuffer(TriangleIndex * 3 + CornerId);
Corners[CornerId].VertexIndex = VertexIndex;
Corners[CornerId].Position = ReadPosition(VertexIndex);
Corners[CornerId].UV = ReadUV(VertexIndex, 0);
}
UNROLL for (CornerId = 0; CornerId < 3; ++CornerId)
{
float3 Position = Corners[CornerId].Position;
float3 EdgeA = Corners[(CornerId + 1) % 3].Position - Position;
float3 EdgeB = Corners[(CornerId + 2) % 3].Position - Position;
Corners[CornerId].Angle = AngleBetweenVectorsFast(EdgeA, EdgeB);
}
// Calculate per triangle information.
FTriangleTangentData TriangleData = CalculateTriangleTangentData(Corners);
// Accumulate the calculated values to each vertex in the output buffer.
UNROLL for (CornerId = 0; CornerId < 3; ++CornerId)
{
// Weight and convert to integer range [-TANGENT_RANGE*PI, TANGENT_RANGE*PI]
float Weight = Corners[CornerId].Angle;
int3 IntTangentZ = (int3)(TriangleData.TangentZ * Weight * TANGENT_RANGE);
int3 IntTangentX = (int3)(TriangleData.TangentX * Weight * TANGENT_RANGE);
int IntOrientation = (int)(TriangleData.Orientation * Weight * TANGENT_RANGE);
// Accumulate each original vertex.
uint VertexIndex = Corners[CornerId].VertexIndex;
uint BaseVertexIndex = VertexIndex * ACCUMULATION_BUFFER_NUM_INTS;
// Buffer set to "Atomic Add" so writing automatically
// adds value to existing values.
WriteAccumulation(BaseVertexIndex + 0, IntTangentZ.x);
WriteAccumulation(BaseVertexIndex + 1, IntTangentZ.y);
WriteAccumulation(BaseVertexIndex + 2, IntTangentZ.z);
WriteAccumulation(BaseVertexIndex + 3, IntTangentX.x);
WriteAccumulation(BaseVertexIndex + 4, IntTangentX.y);
WriteAccumulation(BaseVertexIndex + 5, IntTangentX.z);
WriteAccumulation(BaseVertexIndex + 6, IntOrientation);
}
}
ComputePerVertexNormals
/*
Execution domain: vertex
*/
// Accumulation resource should be NumVertices * 8.
#define ACCUMULATION_BUFFER_NUM_INTS 8
KERNEL
{
if (Index > ReadNumThreads().x)
return;
uint VertexIndex = Index;
float3 TangentX, TangentZ;
uint BaseVertexIndex = VertexIndex * ACCUMULATION_BUFFER_NUM_INTS;
TangentZ.x = (float)ReadAccumulation(BaseVertexIndex + 0);
TangentZ.y = (float)ReadAccumulation(BaseVertexIndex + 1);
TangentZ.z = (float)ReadAccumulation(BaseVertexIndex + 2);
TangentX.x = (float)ReadAccumulation(BaseVertexIndex + 3);
TangentX.y = (float)ReadAccumulation(BaseVertexIndex + 4);
TangentX.z = (float)ReadAccumulation(BaseVertexIndex + 5);
float Orientation = ReadAccumulation(BaseVertexIndex + 6) <= 0 ? -1 : 1;
// We don't need to rescale because we normalize.
TangentX = normalize(TangentX);
TangentZ = normalize(TangentZ);
// gram-schmidt orthonormalization
TangentX = normalize(TangentX - (dot(TangentX, TangentZ) * TangentZ));
// No need to orthogonalize after blending as vertex factory will do so later on.
TangentX = normalize(TangentX);
TangentZ = normalize(TangentZ);
WriteOutPosition(VertexIndex, ReadPosition(VertexIndex));
WriteOutTangentX(VertexIndex, float4(TangentX, 0.0f));
WriteOutTangentZ(VertexIndex, float4(TangentZ, Orientation));
}
Gram-Schmidt orthonormalization visualized
Since 'n' is a unit vector then 'dot(n,t)' is the length of the projection of 't' onto 'n'
Limitation
Geometry must be manifold
Disconnected geometry won't be processed correctly by the smoothing pass:
More advanced smoothing algorithm with robust Laplacian is needed to handle this corner case. Or just fix the model to be water-tight.
Heavy computation
Direct Delta Mush is a much more efficient method which should be considered in case speed is an issue (most likely it will...)
No comments