[Deformer Graph] Lattice deformer in Unreal Engine
Analysis of the deformer graph for free form deformation (FFD, Bezier grid) - 03/2025 - #Unreal, Jumble
Lattice deformation
Basic algorithm for FFD (Free Form Deformation) or 3D lattice deformation. First we consider a vertex $v_\text{world}$ of our mesh in rest pose and in world coordinates. At first this vertex should lie inside our cubic volume
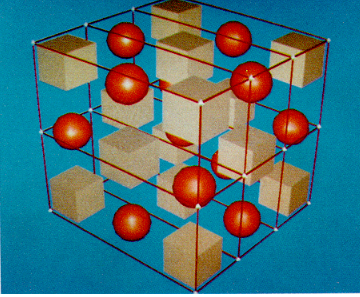
Next we determine the normalized parametric coordinates $S$, $T$, $U$ of our lattice. In other word we'd like to know the coordinates of $v_\text{world}$ inside the volume where $S$ is along the $\vec x$ axis, $T$ the $\vec y$ axis and $U$ the $\vec z$. In addition the parameters $S$, $T$, $U$ are normalized which means they range in $[0.0, 1.0]$:
$$ \begin{aligned} S &= v_\text{world}.x / \text{size}_x \\ T &= v_\text{world}.y / \text{size}_y \\ U &= v_\text{world}.z / \text{size}_z \\ \end{aligned} $$Once you know this computing the new deformed position is just a matter of computing the 3D bezier tensor product as follows:
Where $B_i^n(s)$ are the Bernstein polynomials and $P_{i,j,k}$ a control point of your 3D lattice.
$$ B_i^n(u)={n \choose i} u^i (1-u)^{n-i} $$Changing the rest pose of the volume
Assuming the world coordinates of the volume is represented with a 4x4 transformation matrix $T$ we can move around the volume accordingly. The new computation can now be done in local coordinates of the volume
$$ v_\text{local} = {\color{grey} M^{-1}} \ . \ v_\text{world} $$ $$ \begin{aligned} S &= v_\text{local}.x / \text{size}_x \\ T &= v_\text{local}.y / \text{size}_y \\ U &= v_\text{local}.z / \text{size}_z \\ \end{aligned} $$ $$ S_\text{local}(s, t, u) = \sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=0}^{m} B_i^n(s) B_j^m(t) B_k^m(t) \ \underbrace{ {\color{grey} M^{-1}} \ . \ P_{i,j,k}}_{\text{assuming } P \text{ is in local coords}} $$Finally since the calculated deformed position is in local coordinates now we need to convert it back to world coordinates:
$$ S(s, t, u) = {\color{grey} M} \ . \ S_\text{local}(s, t, u) $$Limitations
As the number of control points increases the Bernstein polynomial degree increases as well and numerical instabilities may arise. One way to alleviate this is to use the de Casteljau's algorithm. But unless you plan on using a high resolution lattice (e.g. 30x30x30) this should not be a concern.
The deformation transition will be $C^0$
Content example - Shader code (DG_LatticeDeformerDemo)
Let's analyze the lattice implementation in the content example project provided by Epic.
The lattice grid resolution and dimensions are provided as inputs
Input struct: S_LatticeDeformerDemo
struct {
Transform transfo;
Vector dimensions;
Int Vector numControls;
Vector[] controlPoints;
}
Kernel code Node: DG_Function_LatticeDeform
// Thomas W. Sederberg and Scott R. Parry. 1986. Free-form deformation of solid geometric models.
#if 0
// No need to have this generalized factorial
float facto(float n)
{
float fac = 1.0;
for (int i = n; i > 0; i--)
fac *= float(i);
return fac;
};
#else
// if you already know how many control points you have
// you can simply cache the values
float facto(float n)
{
if( n < 2.0)
return 1.0;
const int fac[8] = { 1, 1, 2, 6, 24, 120, 720, 5040};
return fac[n];
};
#endif
// Slow bernstein polynom evaluation
// Maybe worth sampling in a 1D texture?
// Or at least use a matrix representation like
// B(t)=[t^3, t^2, t, 1] M P (Horner’s method)
// To precompute the polynom's coefficients.
// @param ni: degree where ni + 1 = nb control points.
// @param ki: control point index
// @param u: normalized [0.0, 1.0] parameter value
float bernstein(int ni, int ki, float u)
{
float n = float(ni);
float k = float(ki);
// This crude way of computing the binomial may be
// numerically unstable for large n and k (e.g. n > 50)<br>
// In practice
float binomial = facto(n) / (facto(k) * facto(n-k));
return binomial * pow(1-u, n-k) * pow(u, k);
};
// Transforms a "point" from world space to local space. (transfo^-1 x {point.xyz, 1})
// Rod: this is only used for the lattice transform and could possibly be inverted
// at the input level i.e. on CPU instead (at the rig control level)
// We compute the inverse of "transfo" by assuming no shear or scale is present
// to optimize its inversion and apply the resulting matrix to "point"
// @param transfo: assume row-matrix representation
// (row-space: v x M)
// - basis vectors set as rows,
// - last row is translation,
// - last column is 0 0 0 1
// @return a point in local space.
float3 transformToLocal(float4x4 transfo, float3 pos)
{
// P_world = Transfo P_local
// P_world = Rot P_local + T_local
// P_local = Rot^-1 (P_world - T_local)
// P_local = Rot^T (P_world - T_local)
// P_local = Rot^T P_world - Rot^T T_local
// first three columns of the matrix represent the rotation part.
float3x3 rot = float3x3(transfo[0].xyz, transfo[1].xyz, transfo[2].xyz);
// The inverse of a rotation matrix is its transpose
// (assuming the transformation matrix is orthonormal == no shear and no scale).
float3x3 invRot = transpose(rot);
float3 invPos = -mul(/*translation part:*/transfo[3].xyz, invRot);
float4x4 inverseTransfo;
inverseTransfo[0] = float4(invRot[0], 0);
inverseTransfo[1] = float4(invRot[1], 0);
inverseTransfo[2] = float4(invRot[2], 0);
inverseTransfo[3] = float4(invPos , 1);
return mul(float4(pos, 1), inverseTransfo).xyz;
};
#if 0
// Column space version, right multiplication.
float3 transformToLocal(float4x4 transfo, float3 pos)
{
float3x3 rot = float3x3(transfo[0][0], transfo[0][1], transfo[0][2],
transfo[1][0], transfo[1][1], transfo[1][2],
transfo[2][0], transfo[2][1], transfo[2][2]);
float3x3 invRot = MatrixInverse(rot);
float3 invTrans = mul(invRot, float3(transfo[0][3], transfo[1][3], transfo[2][3]));
return mul(invRot, pos) - invTrans;
}
#endif
bool withinBounds(float3 minPos, float3 maxPos, float3 pos)
{
return pos.x >= minPos.x && pos.y >= minPos.y && pos.z >= minPos.z &&
pos.x <= maxPos.x && pos.y <= maxPos.y && pos.z <= maxPos.z;
};
KERNEL {
if (index >= readNumThreads().x)
return;
float3 position = readPosition(index);
float4 fullTangentX = readTangentX(index);
float4 fullTangentZ = readTangentZ(index);
float3 tangentX = fullTangentX.xyz;
float3 tangentZ = fullTangentZ.xyz;
fs_LatticeDeformerDemo lattice = readLatticeStruct();
if (lattice.numCtrlPoints.x == 0)
{
writeOutPosition(index, position);
writeOutTangentX(index, fullTangentX);
writeOutTangentZ(index, fullTangentZ);
return;
}
float4x4 latticeTransform = lattice.transfo;
float delta = 1.0f;
float3 localPos = transformToLocal(latticeTransform, position);
const float3 localminPos = float3(0,0,0);
const float3 localmaxPos = lattice.dimensions;
const float3 x0 = localminPos;
if (!withinBounds(localminPos, localmaxPos, localPos))
{
writeOutPosition(index, position);
writeOutTangentX(index, fullTangentX);
writeOutTangentZ(index, fullTangentZ);
return;
}
float3 localTx = localPos + tangentX * delta;
float3 localTz = localPos + tangentZ * delta;
// Convert our vertex position to
// "normalized local lattice coordinates"
// we denote it as "stu" for parametric coordinates S, T, U.
// of our 3D parametric function:
// lattice(S, T, U) => point in 3D space
float3 stu = (localPos - x0) / lattice.dimensions;
float3 stu_Tx = (localTx - x0) / lattice.dimensions;
float3 stu_Tz = (localTz - x0) / lattice.dimensions;
// Final output after deformation.
float3 deformedPos = float3(0,0,0);
float3 deformedTx = float3(0,0,0);
float3 deformedTz = float3(0,0,0);
// Bernstein polynoms degrees
const int degX = lattice.numCtrlPoints.x - 1;
const int degY = lattice.numCtrlPoints.y - 1;
const int degZ = lattice.numCtrlPoints.z - 1;
for (int z = 0; z < lattice.numCtrlPoints.z; z++) {
for (int y = 0; y < lattice.numCtrlPoints.y; y++) {
for (int x = 0; x < lattice.numCtrlPoints.x; x++) {
// Get linear index of the control point
// As opposed to the 3D index represented by (x, y, z)
int cpIndex = x +
y * lattice.numCtrlPoints.x +
z * lattice.numCtrlPoints.x * lattice.numCtrlPoints.y;
float3 controlPoint = lattice.controlPoints[cpIndex];
float3 localControlPoint = transformToLocal(latticeTransform, controlPoint);
float3 stu_controlPoint = localControlPoint - x0;
deformedPos += bernstein(degZ, z, stu.z) *
bernstein(degY, y, stu.y) *
bernstein(degX, x, stu.x) *
stu_controlPoint;
deformedTx += bernstein(degZ, z, stu_Tx.z) *
bernstein(degY, y, stu_Tx.y) *
bernstein(degX, x, stu_Tx.x) *
stu_controlPoint;
deformedTz += bernstein(degZ, z, stu_Tz.z) *
bernstein(degY, y, stu_Tz.y) *
bernstein(degX, x, stu_Tz.x) *
stu_controlPoint;
}
}
}
// put back local deformed position in world coordinates:
position = mul(float4(deformedPos + x0, 1), latticeTransform).xyz;
tangentX = deformedTx - deformedPos;
tangentZ = deformedTz - deformedPos;
// orthonormalize tangent/normal vectors
tangentZ = normalize(tangentZ);
tangentX = tangentX - tangentZ * dot(tangentX, tangentZ);
tangentX = normalize(tangentX);
fullTangentX.xyz = tangentX;
fullTangentZ.xyz = tangentZ;
writeOutPosition(index, position);
writeOutTangentX(index, fullTangentX);
writeOutTangentZ(index, fullTangentZ);
}// END KERNEL
Graph setup and input data
TODOShader code -- hard coded 3x3x3
The animator kit plugin also provides a static lattice deformer.
int FromIndex3d(int3 Index3d)
{
int3 NumPoints = ReadNumPoints();
return Index3d.z * NumPoints.x * NumPoints.y + Index3d.y * NumPoints.x + Index3d.x;
}
float CubicInterp(float A, float B, float T)
{
return lerp(A, B, smoothstep(0,1,T));
}
bool IsValidCorner(int3 Index3d)
{
int3 NumPoints = ReadNumPoints();
return Index3d.x >= 0 && Index3d.y >= 0 && Index3d.z >= 0 &&
Index3d.x < NumPoints.x && Index3d.y < NumPoints.y && Index3d.z < NumPoints.z;
}
KERNEL
{
if (Index >= ReadNumThreads().x) return;
float3 Position = ReadPosition(Index);
int3 NumPoints = ReadNumPoints();
// Dimensions in local space
float3 Dimensions = ReadDimensions();
float4x4 ToWorld = ReadTransform();
float3 NewPosition = Position;
// Do not deform if lattice data is invalid
if (NumPoints.x != 0)
{
float4x4 ToLocal = MatrixInverse_Affine(ToWorld);
float3 LocalPosition = MatrixTransformPosition(ToLocal, Position);
float3 HalfDimensions = Dimensions / 2;
LocalPosition += HalfDimensions;
float3 CellSize = Dimensions/(NumPoints-1);
int3 MinCorner = floor(LocalPosition / CellSize);
{
int3 Corner000 = MinCorner + int3(0,0,0);
int3 Corner100 = MinCorner + int3(1,0,0);
int3 Corner010 = MinCorner + int3(0,1,0);
int3 Corner110 = MinCorner + int3(1,1,0);
int3 Corner001 = MinCorner + int3(0,0,1);
int3 Corner101 = MinCorner + int3(1,0,1);
int3 Corner011 = MinCorner + int3(0,1,1);
int3 Corner111 = MinCorner + int3(1,1,1);
float3 Pos_Corner000 = IsValidCorner(Corner000) ? ReadPoints()[FromIndex3d(Corner000)] + HalfDimensions : Corner000 * CellSize;
float3 Pos_Corner100 = IsValidCorner(Corner100) ? ReadPoints()[FromIndex3d(Corner100)] + HalfDimensions : Corner100 * CellSize;;
float3 Pos_Corner010 = IsValidCorner(Corner010) ? ReadPoints()[FromIndex3d(Corner010)] + HalfDimensions : Corner010 * CellSize;;
float3 Pos_Corner110 = IsValidCorner(Corner110) ? ReadPoints()[FromIndex3d(Corner110)] + HalfDimensions : Corner110 * CellSize;;
float3 Pos_Corner001 = IsValidCorner(Corner001) ? ReadPoints()[FromIndex3d(Corner001)] + HalfDimensions : Corner001 * CellSize;;
float3 Pos_Corner101 = IsValidCorner(Corner101) ? ReadPoints()[FromIndex3d(Corner101)] + HalfDimensions : Corner101 * CellSize;;
float3 Pos_Corner011 = IsValidCorner(Corner011) ? ReadPoints()[FromIndex3d(Corner011)] + HalfDimensions : Corner011 * CellSize;;
float3 Pos_Corner111 = IsValidCorner(Corner111) ? ReadPoints()[FromIndex3d(Corner111)] + HalfDimensions : Corner111 * CellSize;;
float3 InitPos_Corner000 = MinCorner * CellSize;
float3 CellPosition = (LocalPosition - InitPos_Corner000) / CellSize;
float3 NewLocalPosition = LocalPosition;
{
float Edge_000_010 = CubicInterp(Pos_Corner000.x , Pos_Corner010.x, CellPosition.y);
float Edge_100_110 = CubicInterp(Pos_Corner100.x , Pos_Corner110.x, CellPosition.y);
float Edge_001_011 = CubicInterp(Pos_Corner001.x , Pos_Corner011.x, CellPosition.y);
float Edge_101_111 = CubicInterp(Pos_Corner101.x , Pos_Corner111.x, CellPosition.y);
float Face_0 = CubicInterp(Edge_000_010, Edge_001_011, CellPosition.z);
float Face_1 = CubicInterp(Edge_100_110, Edge_101_111, CellPosition.z);
NewLocalPosition.x = lerp(Face_0, Face_1, CellPosition.x);
}
{
float Edge_000_100 = CubicInterp(Pos_Corner000.y , Pos_Corner100.y, CellPosition.x);
float Edge_010_110 = CubicInterp(Pos_Corner010.y , Pos_Corner110.y, CellPosition.x);
float Edge_001_101 = CubicInterp(Pos_Corner001.y , Pos_Corner101.y, CellPosition.x);
float Edge_011_111 = CubicInterp(Pos_Corner011.y , Pos_Corner111.y, CellPosition.x);
float Face_0 = CubicInterp(Edge_000_100, Edge_001_101, CellPosition.z);
float Face_1 = CubicInterp(Edge_010_110, Edge_011_111, CellPosition.z);
NewLocalPosition.y = lerp(Face_0, Face_1, CellPosition.y);
}
{
float Edge_000_010 = CubicInterp(Pos_Corner000.z , Pos_Corner010.z, CellPosition.y);
float Edge_100_110 = CubicInterp(Pos_Corner100.z , Pos_Corner110.z, CellPosition.y);
float Edge_001_011 = CubicInterp(Pos_Corner001.z , Pos_Corner011.z, CellPosition.y);
float Edge_101_111 = CubicInterp(Pos_Corner101.z , Pos_Corner111.z, CellPosition.y);
float Face_0 = CubicInterp(Edge_000_010, Edge_100_110, CellPosition.x);
float Face_1 = CubicInterp(Edge_001_011, Edge_101_111, CellPosition.x);
NewLocalPosition.z = lerp(Face_0, Face_1, CellPosition.z);
}
NewLocalPosition -= HalfDimensions;
NewPosition = MatrixTransformPosition(ToWorld, NewLocalPosition);
}
}
float MaskValue = ReadMask(Index);
MaskValue = ReadMask_Invert() == 1 ? 1 - MaskValue : MaskValue;
float3 Delta = NewPosition - Position;
Delta = Delta * ReadWeight() * MaskValue;
WriteOutPosition(Index, Position + Delta);
}
Squash and stretch
Node: DG_Function_SquashStretch
#ifndef KINDA_SMALL_NUMBER
#define KINDA_SMALL_NUMBER 1e-4f
#endif
#ifndef PI
#define PI 3.1415926535897932f
#endif
void DrawPlane(float3 Position, float3 TangentX, float3 TangentY, float Size, float4 Color)
{
ReadDebugDraw().AddQuad(
Position + (- TangentX + TangentY ) * Size,
Position + (+ TangentX + TangentY ) * Size,
Position + (+ TangentX - TangentY ) * Size,
Position + (- TangentX - TangentY ) * Size,
Color);
}
float BulgeFunction(float InterpolationParam)
{
// Creates a bulge between 0 and 1;
return PI / 2 * sin(PI * InterpolationParam);
}
float QuadraticBezierInterpolation(float InterpolationParam, float ZBias)
{
// Mid control point for the quadratic bezier curve that starts at 0,0 and ends at 1,1
float2 Mid = float2(ZBias, 1-ZBias);
if (Mid.x != 0.5)
{
float t = (Mid.x - sqrt(InterpolationParam - 2 * InterpolationParam * Mid.x + Mid.x * Mid.x))/(-1 + 2 * Mid.x);
return 2*(1-t)*t * Mid.y + t*t;
}
return InterpolationParam;
}
float Sanitize(float Value)
{
return clamp(Value, KINDA_SMALL_NUMBER, 1-KINDA_SMALL_NUMBER);
}
// Note: shader code for demo purpose and is not optimized
// Barr, Alan H. "Global and local deformations of solid primitives."
float3 Deform(float3 Position, uint bDebugDraw)
{
float LengthToDeform = ReadLengthToDeform();
// Factor range [0, +infinity]
float Factor = ReadStretchFactor();
float StretchRatioZ = max(Factor * 2, KINDA_SMALL_NUMBER);
float4x4 LocalToGlobal = ReadOriginTransform();
float4x4 GlobalToLocal = MatrixInverse_Affine(LocalToGlobal);
// Convert to local space and apply the deformation along the local z axis
float3 LocalPosition = MatrixTransformPosition(GlobalToLocal, Position);
// Things outside of limit are considered rigid
float LowerLimit = Sanitize(ReadOptional_LimitFromBottom()) * LengthToDeform;
float UpperLimit = Sanitize(1-ReadOptional_LimitFromTop()) * LengthToDeform;
float ClampedZ = clamp(LocalPosition.z, LowerLimit, UpperLimit);
float InterpolationZ = (ClampedZ - LowerLimit) / (UpperLimit - LowerLimit);
// Shift the bulging center along Z axis
float ZBias = ReadZBias();
float BiasedInterpolationZ = QuadraticBezierInterpolation(InterpolationZ, ZBias);
// Bulge based on how much it is stretched/squashed
float2 BulgeRatio = sqrt(1/(StretchRatioZ));
// Controls which axis should deform more to preserve volume
// [0, 0.5] for favoring X axis and [0.5, 1] favors Y axis
float XYBias = Sanitize(ReadXYBias());
float LinearWeight = 1 - abs(XYBias - 0.5) / 0.5;
float MinMultiplier = 1/BulgeRatio.x;
float MultiplierA = lerp(MinMultiplier, 1, LinearWeight);
float MultiplierB = 1/MultiplierA;
float XMultiplier = XYBias < 0.5 ? MultiplierB : MultiplierA;
float YMultiplier = XYBias < 0.5 ? MultiplierA : MultiplierB;
BulgeRatio.x *= XMultiplier;
BulgeRatio.y *= YMultiplier;
float Bulge = BulgeFunction(BiasedInterpolationZ);
float3 NewLocalPosition;
NewLocalPosition.x = LocalPosition.x * ((BulgeRatio.x - 1) * Bulge + 1);
NewLocalPosition.y = LocalPosition.y * ((BulgeRatio.y - 1) * Bulge + 1);
NewLocalPosition.z =
max(0, LocalPosition.z-UpperLimit) +
(ClampedZ-LowerLimit) * StretchRatioZ +
min(LowerLimit, LocalPosition.z);
float3 NewPosition = MatrixTransformPosition(LocalToGlobal, NewLocalPosition);
if (bDebugDraw)
{
float3 CaptureOrigin = LocalToGlobal._41_42_43;
float3 CaptureDirection = LocalToGlobal._31_32_33;
float3 XAxis = LocalToGlobal._11_12_13;
float3 YAxis= LocalToGlobal._21_22_23;
ReadDebugDraw().AddLine(CaptureOrigin, CaptureOrigin + CaptureDirection * LengthToDeform, float4(0,0,1,1));
float3 LowerLimitGlobalSpace = CaptureOrigin + CaptureDirection * LowerLimit;
float3 UpperLimitGlobalSpace = CaptureOrigin + CaptureDirection * LowerLimit + CaptureDirection * (UpperLimit - LowerLimit) * StretchRatioZ;
DrawPlane(LowerLimitGlobalSpace, XAxis, YAxis, 30, float4(0,0,1,1));
ReadDebugDraw().AddLine(LowerLimitGlobalSpace, LowerLimitGlobalSpace + XAxis * 30, float4(1,0,0,1));
ReadDebugDraw().AddLine(LowerLimitGlobalSpace, LowerLimitGlobalSpace + YAxis * 30, float4(0,1,0,1));
DrawPlane(UpperLimitGlobalSpace, XAxis, YAxis, 30, float4(0,0,1,1));
ReadDebugDraw().AddLine(UpperLimitGlobalSpace, UpperLimitGlobalSpace + XAxis * 30, float4(1,0,0,1));
ReadDebugDraw().AddLine(UpperLimitGlobalSpace, UpperLimitGlobalSpace + YAxis * 30, float4(0,1,0,1));
float BulgePointBiasedInterpolationParam = QuadraticBezierInterpolation(0.5, ZBias);
float3 BulgePointGlobalSpace =
CaptureOrigin +
CaptureDirection * LowerLimit +
CaptureDirection * (((1-BulgePointBiasedInterpolationParam)*UpperLimit +
(BulgePointBiasedInterpolationParam)*LowerLimit) - LowerLimit) * StretchRatioZ;
float3 BulgedXaxis = XAxis * BulgeRatio.x;
float3 BulgedYaxis = YAxis * BulgeRatio.y;
DrawPlane(BulgePointGlobalSpace, BulgedXaxis, BulgedYaxis, 30, float4(0,0,1,1));
ReadDebugDraw().AddLine(BulgePointGlobalSpace, BulgePointGlobalSpace + BulgedXaxis * 30, float4(1,0,0,1));
ReadDebugDraw().AddLine(BulgePointGlobalSpace, BulgePointGlobalSpace + BulgedYaxis * 30, float4(0,1,0,1));
}
return NewPosition;
}
KERNEL
{
if (Index >= ReadNumThreads().x) return;
float3 Position = ReadPosition(Index);
// Value of WeightMap can either come from a float constant node
// or come from a vertex attribute node referencing a vertex attribute
// map created in the skeletal mesh editing tool -> Edit Skin Weights
// -> Edit Attribute/Paint Map. Make sure it is also enabled for rendering
// under "LODInfo". Details may change in the future
float Weight = ReadWeightMap(Index);
float3 NewPosition = Position;
if (Weight >= KINDA_SMALL_NUMBER)
{
// Only use 1 thread to draw debug info
uint bDebugDraw = Index == 0 && ReadOptional_EnableDebugDraw() != 0;
NewPosition = Deform(Position, bDebugDraw);
NewPosition = lerp(Position, NewPosition, Weight);
}
WriteOutPosition(Index, NewPosition);
}
References
- https://www.dgp.toronto.edu/~karan/mprime_project_website/presentations/eg2.pdf
Donate
No comments