Visualizing the inverse theorem

The gist
The inverse function theorem is a an elegant observation stemming from the symmetry of functions and their inverse along the \(y=x\) axis.
Consider a function \(y = f(x)\) and its inverse \(x = g(y) \), the inverse theorem states that you can compute \( g'(y) \) purely based on \(f'\) without prior knowledge of \(g\) (notice, but temporarly ignore that the equality below links two seemingly unrelated variables):
$$ g'({\color{red} y }) = \frac{1}{f'({\color{green} x })} $$This is a pretty neat fact, it means when you can't find the inverse \(g\) you can still easily deduce its tangent \(g'\) from the original function \(f\).
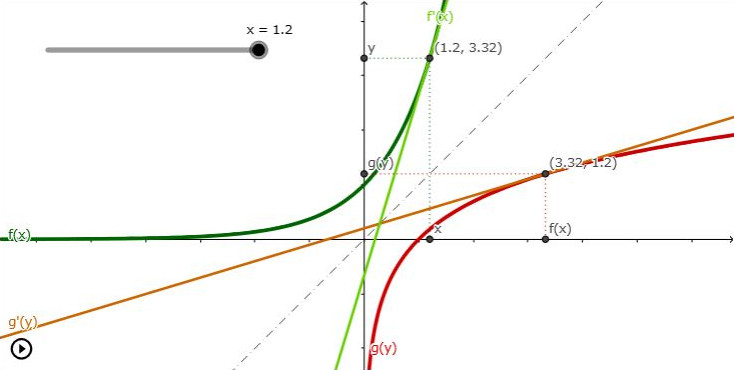
Geometric interpretation
The crux is that the inverse of the tangent \( g' \) is the mirrored version of \(f' \), which allows us to say \( g' = 1 / f' \). So in practice, let's set x to some value and compute the tangent \(f'\) at some point \((x, \ y = f(x))\). The the inverse theorem then tells us, \(g' = 1/f' \), however, where do you think this tangent should lie \((\cdots, \cdots)\) ? Certainly not at \((x, \ y)\)! Well, it actually goes through the mirrored point \( (y, \ x) \). Just switching coordinates gives you the location of the inverse tangent \(g'\). What's more is that just setting \(x\) allows us to know \(y = f(x)\), nowhere did we need \(g\). This can be summarized by the equality below:
$$ g'(f(x)) = \frac{1}{f'(x)} $$Let's rephrase the above to help things sink in. We want to find the tangent of \(f\) and \(g\) but only given a variable \(x\). So far we know that \(g'({\color{red} y }) = {1} / {f'({\color{green} x })}\) but how do we deduce the right \({\color{red} y }\) that corresponds to the tangent \(g'\) of the inverse \(g\)? Well this is given by \( y = f(x) \).
Deriving the inverse theorem
Using the chain rule and the fact that \(g(f(x)) = x\) it's simple to derive:
$$ \begin{aligned} g\big ( { \color{darkblue} f(x)} \big ) & = x \\ \Rightarrow \Big [ g\big ({ \color{darkblue} f(x)}\big) \Big ]' & = \Big [ x \Big ]'\\ g'\big ({ \color{darkblue} f(x)}\big) . f'(x) & = 1 \\ g'\big ({ \color{darkblue} f(x)}\big) & = \frac{1}{f'(x)} \\ \end{aligned} $$Variation
By definition of the inverse \(f\) and \(g\) can be swapped:
$$ \begin{aligned} f\big (g(x) \big ) & = x \\ \Rightarrow f'\big ({ g(y)}\big) &= \frac{1}{g'(y)} \end{aligned} $$Leibniz tricks
This one is neat, when using Leibniz notation to designate derivatives, it is very intuitive to get back the inverse theorem:
$$ \frac{ \d x}{\d {\color{red} y}} = \frac{1}{{\d y}\over{\d {\color{green} x}}} \Annotation{ \text{ thinking in terms rate change between variables: } \\ x = g(y) \text{ and } y = f(y)} $$We can see the above trick as renaming \(f:y\) and \(g:x\) :
$$ \begin{aligned} \frac{ \d g}{\d y} \quad & = \quad \frac{1}{{\d f}\over{ \d x}}\\ \frac{ \d \big( g(y) \big) }{\d y} & = \frac{1}{{\d\big(f(x)\big)}\over{\d x}} \\ g'(y) \quad & = \quad \frac{1}{ f'(x) } \\ \end{aligned} $$Notice also the notation is a tad abusive because the equality only holds because we have hidden information:
\[ \frac{ \d x}{\d {\color{red} y}} = \frac{ \d x(\text{...}) }{\d {\color{red} y}} = \frac{ \d x( y ) }{\d {\color{red} y}} = \frac{ \d x( {\color{red} y} = f({\color{green} x}) ) }{\d {\color{red} y}} = g'( f({\color{green} x})) = \frac{1}{{\d y}\over{\d {\color{green} x}}} = \frac{1}{ f'({\color{green} x}) } \]Consider \(h_i: \mathbb R \rightarrow \mathbb R\); when making use of the Leibniz trick, keep in mind this change the input variable you use to evaluate the expression:
$$ h_1({\color{red} y}) = \frac{ \d x}{\d {\color{red} y}} $$ $$ h_2({\color{green} x}) = \frac{1}{{\d y}\over{\d {\color{green} x}}} $$But that might turn out ok since we can always find a \(y\) according to an \(x\) with the original function \(y = f(x)\):
$$ h_1\big (f({\color{green} x}) \big) = h_2({\color{green} x}) = \frac{1}{{\d y}\over{\d {\color{green} x}}} $$ $$ h_2\big (g({\color{red} y}) \big) = h_1({\color{red} y}) = \frac{ \d x}{\d {\color{red} y}} $$Proper theorem
This is the exact definition of the inverse theorem.
If \(f\) is differentiable at \(c\), \(f'\) is continuous at \(c\), and \(f'(c) \neq 0\), there is an interval \(I\) containing \(c\) on which \(f^{-1}\) exists and is differentiable. Moreover:
$$ {f^{\scriptscriptstyle -1}}^{\displaystyle'}\big (f(c) \big) = \frac{1} {f^{\displaystyle \prime} (c)} $$Example
Consider:
$$ f(x) = e^x + x^3 + x $$The inverse \(f^{-1}\) does not have a nice closed form expression but we can still compute \(f'^{-1}\) if we set \(c\); for instance \(c= 0\)
- \(f(0) = 1\)
- \(f'(x) = e^x + 3 x^2 + 1\)
- \(f'(0) = 1 + 1 = 2\)
The crux really lies in the fact we evaluate \({f^{\scriptscriptstyle -1}}^{\displaystyle'}(1)\) at 1 and not at 0.
Reference
- Inverse theorem video explanation (University of Toronto Mississauga)
- Khan academy explanation
Images
No comments
 Donate
Donate