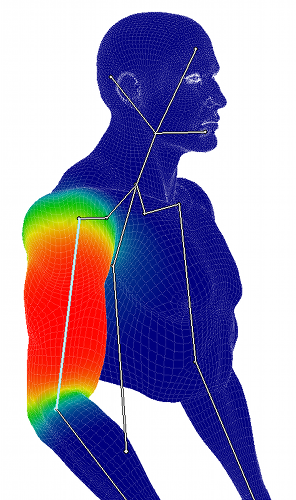
手動か自動でもそれぞれのジョイントの影響値（又はスキン　ウェイト）がメッシュの部分に割り当てられます。 骨の影響と運動によってメッシュを動かすことが出来ます。 上の画像は1つの骨の影響を示しています。 赤いエリアですとメッシュ頂点に割り当たった骨の重みを「1.0」と表します（そのメッシュの一部は完全に骨との運動を一致します） 反対に、青いエリアのウェイト値は「0.0」となるので、ジョイントの影響はありません（メッシュはこのジョイントによって動きません） 緑エリアは「0.5」の中間影響を意味します。 各骨は、メッシュ全体にウェイトを定義します。 通常の場合はメッシュをスムーズに変形させる為、スキン　ウェイトはお互いに重なり合っています。 LBSの数式は下記の通りです

$$ \begin{equation} \bar{\mathbf{p_i}} = \sum_{j=1}^{n} w_{ij} T_j \mathbf{p_i} \end{equation} $$

ここで

• 「\(n\)」は骨の数。（整数）
• 「\(w_{ij}\)」はスキン　ウェイトを表す実数です。i 番目の頂点に対する j 番目のジョイントの影響値です。
• 「\(T_j\)」グローバル座標系における4x4の行列です。\(T_j\)はj 番目の骨のバインド ポーズ（又は「Rest Pose」、「T-pose」）の変形を定義します。
• 「 \(\mathbf{p_i}\)」バインド　ポーズ・入力の頂点位置。
• 「 \(\bar{\mathbf{p_i}}\)」変形後・出力の頂点位置。

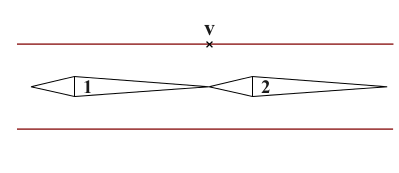
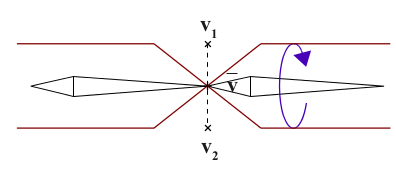
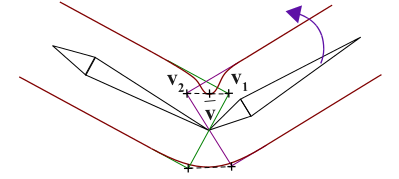
ここでは、中心となる頂点\(\mathbf v\)は、両方の骨から等しく影響を受けるため、\(w_{i1} = w_{i2} = 0.5\)となります。 LBSの数式にこの数字を入れてみましょう。

\[
\begin{eqnarray*}
\bar{\mathbf{v}} &= & \sum_{j=1}^{n} w_j T_j \mathbf{v} \\
                             &= & w_1 (T_1 . \mathbf v) + w_2 (T_2 . \mathbf v) \\
                             &= & 0.5 \mathbf{v_1} + 0.5 \mathbf{v_2}
\end{eqnarray*}
\]

上の数式を見ると\(\mathbf v_1\) と \(\mathbf v_2\) の線形補間が行われることが明らかになります。線形補間によって、不適切な位置が計算されます。 なぜボリュームダウンの現象が起こる理由をより良く理解する為、行列を解釈してみましょう。

$$
\begin{eqnarray*}
\bar{\mathbf{v}} &= & \sum_{j=1}^{n} w_j T_j \mathbf{v} \\
                             &= & (w_1 . T_1  + w_2 . T_2) . \mathbf v \\
                             &= & M . \mathbf v
\end{eqnarray*}
$$

たとえ、\(T_1\)と\(T_2\)が剛体変換であったとしても、重み付けされた変形の組み合わせが剛体変換であることは保証出来ません。(剛体変換とは回転と平行移動のみを表現できることです)。 ところで、\(M\)にはスケール因子が入ってしまうことが多く、それが縮みの原因になっています。\(T_j\)の計算の詳細はこちらです。

デュアルクォータニオンスキニング

初めに

ボリュームの消失問題を回避したければ、LBSの代わりにDQSはとても良い代替アルゴリズムです。 LBSとDQSの処理速度はほぼ同じく、数学さえを把握すれば、実装も安易です。 DQSは多数のソフト （例：Maya, 3D Studio Max、 Blender） で実装されてるので、具体的にどんな風にメッシュを動かしてるのか試すことが出来ます。

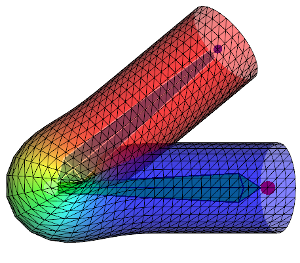
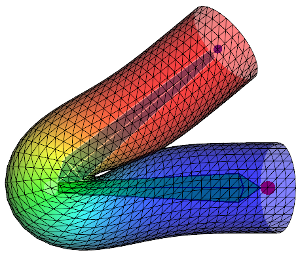
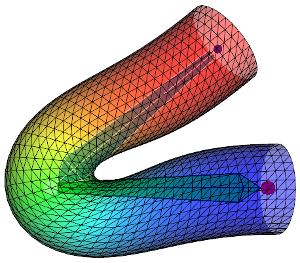
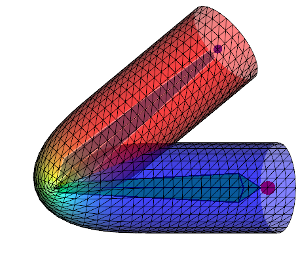
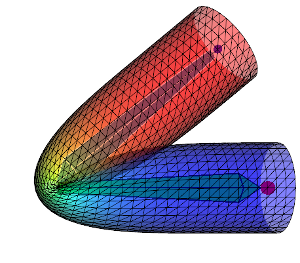
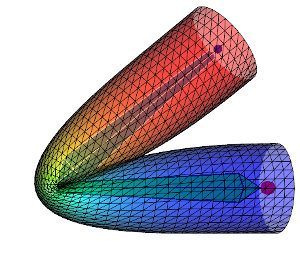
下記の画像では異なるスキン　ウェイトの影響で、DQSとLBSを比較します。

Dual Quats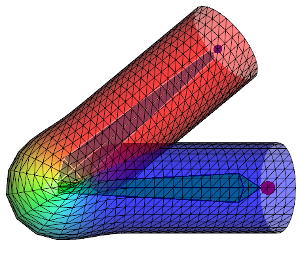
Linear  Blend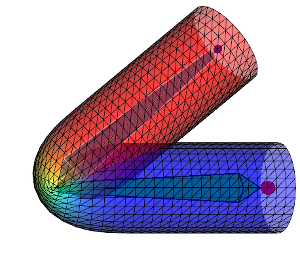
スキン　ウェイト　拡散・滑らかさ	+	++	+++	++++

1行目はDQS、2行目はLBSを示している。 左から右へ、スキン　ウェイト影響がますます拡散して行きます。 ウェイトを拡散させるとより重なっていって、変形がよりスムーズになります。 ウェイトがどのように拡散されるかによって、変形された形状が大きく変わります。 頂点位置が骨の線分から離れるに伴い、ウェイト「\(w_{ij}\)」の関数はより減少し、減り方によって（例：線形、二次的に）メッシュの形状が変わって行きます。 と言うわけで、私のコードで上記の画像を再現出来るためには、全く同じウェイト値にする必要があります。

原理

なぜ、「デュアルクォータニオンスキニング」を使うことで、ボリュームの消失問題が改善出来るのか、直感的に解説してみます。 以下の図で概念を掴んでみましょう。

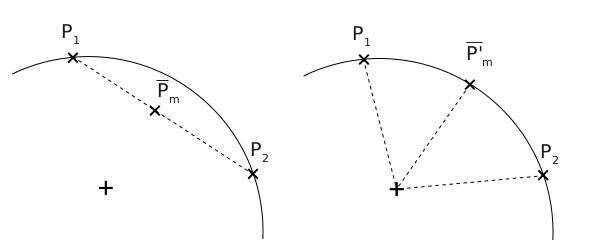
左は、2つの頂点にLBSが適用した結果です。 直線補間なので、新しい位置は\(\mathbf{p_1}\)と\(\mathbf{p_2}\)の線分の間のどこかになります. 右はDQS。線形補間ではなく、球面線形補間（Slerp）ですと！ LBSとは異なり、新しい位置は円弧上にあるため、メッシュの縮みを避けることができます。

では、DQSはどのように実装されるのでしょうか？ LBSの場合、ジョイントの動きを表現するために行列を使用するのですが、DQSではDual Quaternions（デュアル　クオータニオン）と呼ばれる数学的対象を利用します。 両方とも回転と平行移動を表現することが出来ます。ただし、行列と異なり、複数のデュアル　クオータニオンを平均すると球面線形補間が行われます。 一旦、詳細を省いて、いくつかの直感的な例を挙げてみます。

• 複素数を使って2次元の回転を表現することを学んだことがありませんか？これは2x2の行列でも表現できます。
• そして、複素数の３次元バージョンはクオータニオンです。3x3の行列と同じように、3次元の回転が表現できます。
• さらに、デュアルクォータニオンでは4x4の行列のように回転と平行移動を表現することができます。

下記のようにDQSによる変形された頂点の位置が計算できます

$$ \mathbf{\dot q} =
\frac{\sum_{i=1}^n w_i \mathbf{\dot q}_i}{\| \sum_{i=1}^n w_i \mathbf{\dot q}_i \|}
$$

ここでは行列をブレンドする代わりに(\( M = \sum_{i=1}^{n} w_i T_i \))デュアルクォータニオンをブレンドします。 \(\mathbf{\dot q}_i\)とは\(w_i\)で重み付けされた骨のデュアルクォータニオン変換です。そして、 ブレンドの結果は\( {\| \sum_{i=1}^n w_i \mathbf{\dot q}_i \|} \)に正規化されます。 デュアルクォータニオン\(\mathbf{\dot q}\)のおかげで頂点をバインドポーズの位置から変形された位置まで変換ができます。 因みに、デュアルクォータニオンのブレンド数式を計算するのに加算、乗算、除算などは必要となります。 また、行列のように頂点にデュアルクォータニオンを適用するのに頂点を変換させる計算方法を定義しなければなりませんが、 全ては提供しているコードに解説されています。 そういった計算を細かく掴まなくても、なぜLBSのブレンドよりデュアルクォータニオンのブレンド数式の方がうまくいくのが理解出来ます。 それは、先ほど言ったようにデュアルクォータニオンのブレンド数式の計算結果は回転と平行移動のみを表すことが保証されることです。、　 つまり、行列のブレンドとは異なり、ジョイント周りのメッシュを縮めるスケールファクターは発生しません。

レシーピ

下記の通り、既存のLBSのコードベースにDQSを導入する必要なポイントです。

1. どうやって、デュアルクォータニオンを表現すればいい？　(8つの実数を使う)
2. どうやって、LBSの4x4行列からデュアルクォータニオンへ変換すればいい？
3. どうやって、デュアルクォータニオンの演算子（* + /など）を計算すればいい？
4. どうやって、デュアルクォータニオンで頂点とベクトルを変換すればいい？

これらの質問に関しては[  提供したC++コード ]での実装の形で答えがあります。 数学的な説明はしないので、興味ある方は論文の 「section 4」にご参照ください

1. 数値表現

デュアルクォータニオンとは、二重数の分類に属しています。 数学における二重数とは、\( \varepsilon^2 = 0 \)を満たす実数\(a\)、\(b\)、\(\varepsilon\)を用いて、\(z=a + \varepsilon b\)と表すことができる数のことです。 （どうやら複素数に似てますよね)。なお、デュアルクォータニオンの場合は\(a\)と\(b\)はクォータニオンになります。

クォータニオンには4つの実数が必要なので、合計は8つの実装

2. 行列からの換算

回転と平行移動を正しく表すためにデュアルクォータニオンの数値の初期化が必要なのですが、 下記のコンストラクタを使えば手軽にできます。

#include "dual_quat_cu.hpp" 
using namespace Tbx;
{
    Transfo mat; // 骨の変形を表す4x4 行列
    Dual_quat_cu dq( mat ); //　行列からデュアルクォータニオンの初期化
}

これにより、回転を表す行列の部分がクォータニオンに変換され、平行移動ベクトルも抽出されます。 クォータニオンとベクトルは、論文で述べられているように、1つのデュアルクォータニオンに変換されます。

3. 演算子

デュアルクォータニオンのブレンドを行うには、デュアルクォータニオンの加算や除算などの計算方法が必要です。 この点についても、論文で十分解説されていますが、理解しなくても提供した「Dual_quat_cu」クラスの演算子オーバーロードが使えます。

4. 変換の適用

デュアルクォータニオンでベクトルを回転させる「rotate()」および頂点を変換させる「transform()」メソッドを提供しています。

変形のソースコード

以下の通り、 デュアルクォータニオン　ブレンドの計算をメッシュに実行する実例です。 怪しい「if」 を気づきになったと思いますが、これは符号を判定する為です。 このテストは、最短の回転経路をとるために行われます。

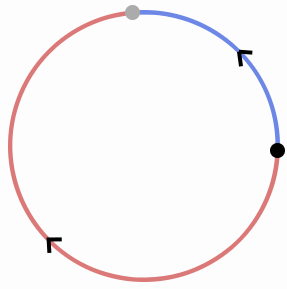
2つのデュアルクォータニオンの内積の符号で、最短経路の決定が出来ます。これについては、論文の「Section 4.1」で説明されています。

#include <vector>
#include "dual_quat_cu.hpp"

using namespace Tbx;

/**
 * @param in_verts : バインド　ポーズの状態でメッシュの頂点
 * (モデル 座標系)
 * @param in_normals : メッシュの法線 ('in_verts'と一緒の　)
 * @param out_verts : dual quaternionsに変形された頂点
 * @param out_normals : dual quaternionsに変形された法線
 * @param dual_quat : 各ジョイントのdual quaternionsリスト
 * (モデル 座標系)
 * @param weights : 各頂点でジョイントの重み・スキン　ウェイトのリスト
 * @param joints_id : 各頂点でジョイントのインデクスのリスト
 * ('weights'と同順)
 */
void dual_quat_deformer(const std::vector<Point3>& in_verts,
                        const std::vector<Vec3>& in_normals,
                        std::vector<Vec3>& out_verts,
                        std::vector<Vec3>& out_normals,
                        const std::vector<Dual_quat_cu>& dual_quat,
                        const std::vector< std::vector<float> >& weights,
                        const std::vector< std::vector<int> >& joints_id)
{
    for(unsigned v = 0; v < in_verts.size(); ++v)
    {
        // 'v'を影響する骨の数
        const int nb_joints = weights[v].size(); 

        if(nb_joints != 0)
        {
            Dual_quat_cu dq_blend = Dual_quat(Quat(0.0f, 0.0f, 0.0f, 0.0f), 
                                              Quat(0.0f, 0.0f, 0.0f, 0.0f));

            int pivot = joints_id[v][0];
            Quat_cu q0 = dual_quat[pivot].rotation();            
            for(int j = 0; j < nb_joints; j++)
            {
                const int k = joints_id[v][j];
                float w = weights[v][j];
                const Dual_quat_cu& dq = (k == -1) ? Dual_quat_cu::identity() : dual_quat[k];
                // 最短の回転経路の判定：
                if( dq.rotation().dot( q0 ) < 0.f )
                    w *= -1.f;

                dq_blend = dq_blend + dq * w;
            }            
        }else{
            dq_blend = Dual_quat::identity();
        }

        // 頂点の最終位置
        Vec3 vi = dq_blend.transform( in_verts[v] ).to_vec3();
        out_verts[v] = vi;
        // 法線の最終向き
        out_normals[v] = dq_blend.rotate( in_normals[v] );
    }
}

下記の通り、LBS（左）とDQS（右）の比較。

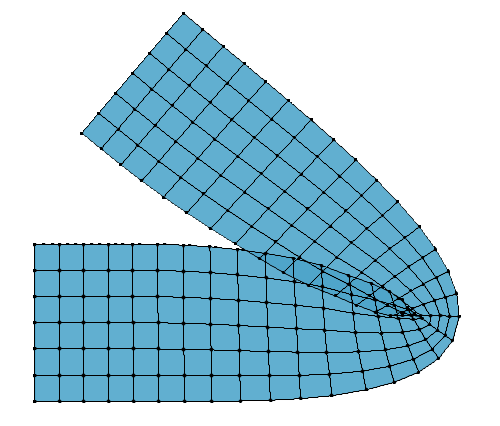
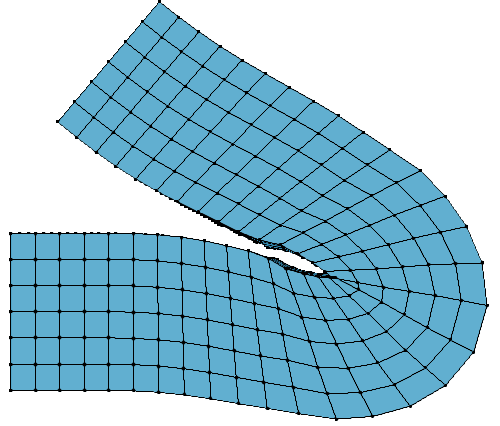
まとめ

DQSは、業界でLBSに次ぐスタンダードとなっています。LBSのボリューム消失問題を避けながら、実行速度もほぼ一緒です。 しかし、DQSのジョイント部分に膨らみが生じる傾向があることにお気づきでしょうか。 元論文はこの欠点について話していませんが、スキン　ウェイトを弄ることで割に抑えられます。 それに、膨らみを抑える手法も発表されたことがあります。 例えば、「quick fix of the Dual Quaternion Skinning bulge artifact」のページではそういった手法のソースコードを提供しています。 また、よりエレガントでロバストな解決策を提供したディズニーの論文もあります。 「 Real-time Skeletal Skinning with Optimized Centers of Rotation. 」 後者の実装の方が少し難しいですが。

なお、DQSはスケール因子を表現できないので、スケールにおける特殊な対応が必要です。 Kavan氏の論文のセクション4.2では、DQSによるスケールおよびシアー変換の処理方法について触れられていますが、 別途でこちらのブログ記事そういった対応を解説しています。

リンク

C library for Dual-Quaternions
A more formal tutorial on Dual Quaternions Skinning
Maya plugin

参照

Geometric Skinning with Approximate Dual Quaternion, Ladislav Kavan & Al

No comments