Unreal Engine C++: FMatrix doc sheet

#include "Math/Matrix.h"
Memory layout
Matrix elements are accessed with:
FMatrix::M[rowIndex][columnIndex]
Therefore FMatrices are row major in memory.
(Since: int array[2][2] = { {0, 1}, {2, 3} };
In memory looks like this: 0 1 2 3)
Representation (CPU)
Recall that the "matrix representation" ≠ "memory layout". You can have a column-major memory layout but a row-matrix representation (basis vectors set as rows)
Ultimately it's only the user that knows how the numbers inside a FMatrices are organized but Unreal's convention is to use a row-matrix representation:
X.x X.y X.z 0.0 // Basis vector X
Y.x Y.y Y.z 0.0 // Basis vector Y
Z.x Z.y Z.z 0.0 // Basis vector Z
T.x T.y T.z 1.0 // Translation vector
FMatrix::setAxis() and methods alike uses row-matrix representation. This can be verified in the constructor as well:
FMatrix44f JointMatrix(
FVector3f(1.0f, 0.0f, 0.0f), // X
FVector3f(0.0f, 1.0f, 0.0f), // Y
FVector3f(0.0f, 0.0f, 1.0f), // Z
FVector3f(0.0f, 0.0f, 0.0f) // Translation
);
template<typename T>
FMatrix44f::FMatrix44f(const FVector3f& InX,
const FVector3f& InY,
const FVector3f& InZ,
const FVector3f& InW)
{
M[0][0] = InX.X; M[0][1] = InX.Y; M[0][2] = InX.Z; M[0][3] = 0.0f;
M[1][0] = InY.X; M[1][1] = InY.Y; M[1][2] = InY.Z; M[1][3] = 0.0f;
M[2][0] = InZ.X; M[2][1] = InZ.Y; M[2][2] = InZ.Z; M[2][3] = 0.0f;
M[3][0] = InW.X; M[3][1] = InW.Y; M[3][2] = InW.Z; M[3][3] = 1.0f;
}
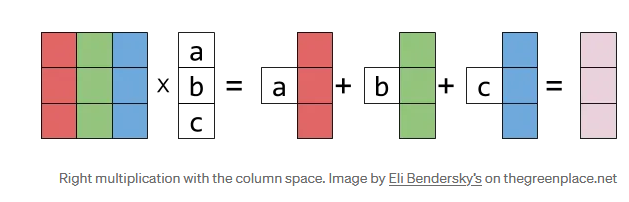
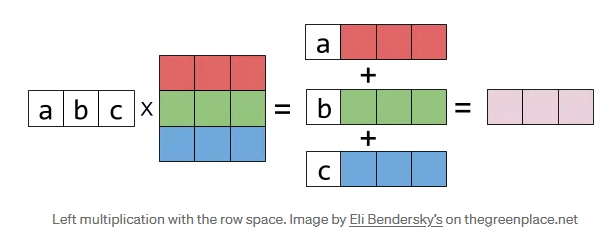
Multiplication
Because FMatrix convention is to use row-matrix representation the order you multiply matrices together is the opposite of the traditional math way:
-
Math (column space representation):
M3 * M2 * M1 * vec
M1 gets applied first and M3 last -
UE (row space representation):
vec * M1 * M2 * M3
for M1 to be applied first multiplication needs to be reversed.
Note that there is nothing particular about the implementation of the multiplication operator:
void FMatrix::mult(int A[N][N], int B[N][N]) {
int C[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
int num = 0;
for (int k = 0; k < N; k++) {
num += A[i][k] * B[k][j];
}
C[i][j] = num;
}
}
}
But since UE lays out the coefficients of the matrix in a transpose way of the conventional math way, we need to reverse the order transforms are usually multiplied.
Representation (GPU/Shader)
Something pretty usual with FMatrix when it gets uploaded to gpu/shader in Unreal code base,
is that it gets transposed and converted to a float3x4
FMatrix44f mat; // fill mat float mat3x4_columnMajor[12]; mat.To3x4MatrixTranspose(/*out: */ mat3x4_columnMajor); // upload mat3x4_columnMajor to gpu
Therefore, usually, the code in the Unreal's shader relies on a column-matrix representation of the transformations
and multiplication happens in the conventional math way: M3 * M2 * M1 * vec
//HLSL float3x4 M1; // First transformation float3x4 M2; // Second transformation vec3 new_position = mul( M2, mul( M1, vec3(position)));
Note: HLSL memory layout is row-major, just like a FMatrix memory layout is row-major.
If we had not transposed it, we would multiply from the left inside the Shader code as well, just like in CPU code.
Blue Print transforms
I have noticed that nodes in BP, control rig, deformer graph etc. mostly use the row space / left hand multiplication
vec * M1 * M2 * M3
Code samples
// Copy constructor / copy operator : FMatrix44f mat = FMatrix44f::Identity; // Set the translation part (last row): mat.M[3][0] = 1.0f; mat.M[3][1] = 0.0f; mat.M[3][2] = 0.0f; // You can set the translation/origin with a method as well: FVector3f pos(10.0, 0.0, 0.0); mat.SetOrigin( pos ); FMatrix44f mat2 = mat; FMatrix44f mat3 = FMatrix44f::Identity; mat3 = mat; mat.M[3][0] = -1.0f; mat.M[3][1] = -1.0f; mat.M[3][2] = -1.0f; // FMatrix is a 4x4 *double matrix: FMatrix m = FMatrix::Identity; m.M[3][0] = -2.0; m.M[3][1] = -2.0; m.M[3][2] = -2.0; FMatrix44f mat4 = FMatrix44f(m); // Convert transform to FMatrix: FTransform tr = FTransform::Identity; mat4 = FMatrix44f( tr.ToMatrixWithScale() ); // FVector is a 3D double vector: FVector pos(1.0, 2.0, 3.0); // multiply against the 4x4 matrix (pox.x, pos.y, pos.z, 1.0) pos = m.TransformPosition( pos );
Produce a rotation matrix
Needs to be checked:
#include "Math/RotationMatrix.h" FVector3f rotationAxis = FVector3f(1.0f, 0.0f, 0.0f).GetSafeNormal(); // Example: X-axis float rotationAngleRad = FMath::DegreesToRadians(45.0f); // Convert 45 degrees to radians FQuat4f quat = FQuat4f(rotationAxis, rotationAngleRad); FMatrix44f mat = FRotationMatrix44f::Make(quat);
FTransform
Attributes
Quat Rotation; //< Rotation as a quaternion Vector Translation; //< Translation as a vector Vector Scale3D; //< 3D scale (always applied in local space) as a vector // Accessors: TQuat q = this->GetRotation() or TRotator r = this->Rotator() TVector v = this->GetTranslation() TVector v = this->GetScale3D()
Transformation order:
Scale -> Rotate -> Translate.
Multiplication order (same as a FMatrix):
vec * T1 * T2 * T3
(i.e. T1 transformation gets applied first and T3 last)
FTransform tr{
FRotator{ 10.0f, 20.0f, 30.0f }, // Rotation around each axis in degrees (y, x ,z)
FVector{ 1.0f, 2.0f, 3.0f }, // Translation
FVector{ 2.0f, 1.0f, 1.0f } // Scale
};
FTransform tr_inv = tr.Inverse();
FTransform identity = tr * tr_inv;
FVector pos = FVector{ 50.0f, 60.0f, 70.0 };
FVector new_pos = tr.TransformPosition( pos );
// WARNING: be sure to use InverseTransformPosition() and not TransformPosition()
// Although each components (rotation, translation, scale) is inverted.
// You must also invert the order you apply the components to truly invert the transformation:
FVector back_to_pos = tr_inv.InverseTransformPosition( new_pos );
// On the other hand when working with FMatrix you don't need to
// pay attention to the above corner case:
FMatrix mat_inv = tr.ToMatrixWithScale().Inverse();
FVector back_to_pos = mat_inv.TransformPosition( new_pos );
No comments
 Donate
Donate