General Leibniz rule Explained
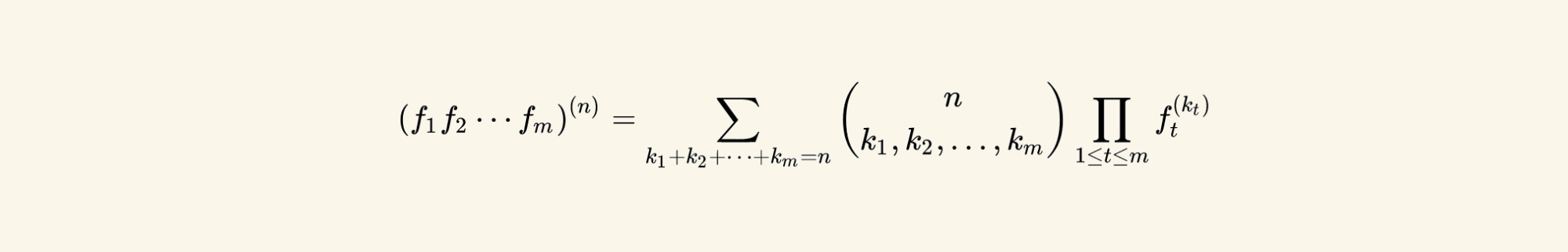
Introduction
I was initially trying to help on interpreting the general Leibniz rule on stackexcange.com, in particular, how to read the peculiar: $$ \sum_{k_1+k_2+\cdots+k_m=n} $$ summation notation used in the General Leibniz rule. As the answer grew longer I decided to make an article out of it. Understanding this notation will also help to read the Multinomial theorem, and as links to combinatorics. Reader should be already familiar with the basic sigma notation $\sum_{i=0}^{m}$
Short explanation
$\sum_{k_1+k_2+\cdots+k_m=n}$ is the sum of all possible combinations of $\{k_1, \ k_2,\ \cdots, k_m\}$ that satisfy ${k_1+k_2+\cdots+k_m=n}$, for instance:
$$ \sum_{\underbrace{k_1+k_2=2}_{\Large \text{equation}}} (k_1, k_2) = \overbrace{\underbrace{(2,0)}_{\text{solution 1}}}^{2+0=2} + \overbrace{\underbrace{(0,2)}_{\text{solution 2}}}^{0+2=2} + \overbrace{\underbrace{(1,1)}_{\text{solution 3}}}^{1+1=2} $$Here $k_m$ must be positive integers i.e. $k_m \in \mathbb N$ and their sum must be equal to $n$.
Long explanation
$$ \sum_{k_1+k_2+\cdots+k_m=n} $$Describes a sum of terms $ (\cdots + \cdots + \cdots) $ just like $\sum_{i=0}^{m}$ does. However, the number of terms is not explicitly written in this version. The number of all possible combinations the set $\{k_1, \ k_2,\ \cdots, k_m\}$ can make, while satisfying ${k_1+k_2+\cdots+k_m=n}$, is the number of terms. In addition, similar to using the $i$ in each terms of $\sum_{i=0}^{m}$, in this version each term can then freely use the value of the set $\{k_1, \ \cdots, k_m\}$.
This notation implies we have to solve the following equation:
$$k_1+k_2+\cdots+k_m=n$$Where $k_1, k_2,\cdots,k_m$ are positive integers. $\sum_{k_1+k_2+\cdots+k_m=n}$ is then understood to be the sum of all tuples that solve the equation, for instance:
$$ \begin{array}{ll} & \{k_1=n, \quad k_2=0,\quad \cdots, \quad k_m=0\} \\ + & \{k_1=0, \quad k_2=n,\quad \cdots, \quad k_m=0\} \\ + & \quad \quad \quad \quad \quad \quad \cdots \end{array} $$for $m=3$, $k=3$ the sum looks like:
$$ \sum_{k_1+k_2+k_3=3} $$Which means we must solve for:
$$k_1+k_2+k_3=3$$This is a combinatorics problem but since we work with an easy example let's first derive all possibilities by hand:
k1 k2 k3
--------
0 0 3
0 3 0
3 0 0
1 1 1
2 0 1
2 1 0
1 2 0
0 2 1
0 1 2
1 0 2
Translated as order of derivatives:
$$ \sum_{k_1+k_2+k_3=3} f^{k_1}.g^{k_2}.h^{k_3} = $$
f(x) g(x) h(x)
----------------
f g h''' +
f g''' h +
f''' g h +
f' g' h' +
f'' g h' +
f'' g' h +
f' g'' h +
f g'' h' +
f g' h'' +
f' g h'' +
Underlying combinatorics
The number of solutions of the Diophantine equation $k_1+k_2+k_3=3$ can be computed thanks to the famous formula:
$$ \begin{align} \quad \binom{m + n - 1}{n} = \binom{3+3-1}{3} = \binom{5}{3} = \frac{5!}{3! \cdot (5 - 3)!} = \frac{5!}{3! \cdot 2!} = 10 \end{align} $$In combinatorics $\binom{m + n - 1}{n}$ represents "the total number of unordered *combination* with repetition". It's a mouth-full to say let's pick $n$ objects among a choice of $m$ bins (each bin contain the same type of objects). Example with 3 bins:
- bin A: full of 'k1' objects
- bin B: full of 'k2' objects
- bin C: full of 'k3' objects
And we can pick only $m=3$ objects, therefore we have 10 combinations:
k1 k2 k3
aaa -> 3a -> 3 0 0
bbb -> 3b -> 0 3 0
ccc -> 3c -> ...
abc -> ...
aac
aab
abb
acc
bbc
bcc
$$
\underbrace{
\overbrace{k_1}^{\text{bin A}} +
\overbrace{k_2}^{\text{bin B}} +
\overbrace{k_3}^{\text{bin C}}
}_{m \text{ bins}}
=
\overbrace{\underbrace{3}_{n}}^{\text{number of objects to pick}}
$$
Coefficients
From there we are only missing the multinomial coefficients which we can derive with:
$$ {n \choose k_1, k_2, \ldots, k_m} = \frac{n!}{k_1!\, k_2! \cdots k_m!} = \frac{(k_1+k_2+ \cdots + k_m)!}{k_1!\, k_2! \cdots k_m!} $$For 3 terms:
$$ \sum_{k_1+k_2+k_3=3} {n \choose k_1, k_2, k_3} f^{k_1}.g^{k_2}.h^{k_3} $$
f(x) g(x) h(x)
----------------
f g h''' +
f g''' h +
f''' g h +
6 f' g' h' +
3 f'' g h' +
3 f'' g' h +
3 f' g'' h +
3 f g'' h' +
3 f g' h'' +
3 f' g h'' +
Explicit formulation with nested sums
As pointed out by @Arthur's answer, this summation notation can be made more explicit:
$$ \sum_{k_1+k_2+\cdots+k_m=n} (k_1, k_2, \cdots, k_m) \\ ~\\ = \\ ~\\ \sum_{k_1=0}^n \ \sum_{k_2=0}^{n-k_1} \ \sum_{k_3=0}^{n-(k_1+k_2)} \cdots \quad \sum_{k_{m-1}=0}^{n-(k_1+k_2+\cdots+k_{m-2})} (k_1, k_2, \cdots, \overbrace{n-(k_1+k_2+\cdots+k_{m-1})}^{k_m}) $$Let's apply the above formulation to our case:
$$ \sum_{k_1+k_2+k_3=3} (k_1, k_2, k_3)= \sum_{k_1=0}^n\sum_{k_2=0}^{n-k_1} (k_1, k_2, \overbrace{(n-k1+k2))}^{k_3} $$Algorithm for 3 terms
Thanks to the explicit nested sum expression, it is possible to compute all possible combinations. In addition, this JavaScript code may be more legible to programmers than the sigma sums:
let n = 3
for(var k1 = 0; k1 <= n; k1++ ){
for(var k2 = 0; k2 <= (n-k1); k2++ ){
var k3 = n - (k1+k2);
console.log(k1+" : "+k2+" : "+k3);
}
}
This will output in the console:
"0 : 0 : 3"
"0 : 1 : 2"
"0 : 2 : 1"
"0 : 3 : 0"
"1 : 0 : 2"
"1 : 1 : 1"
"1 : 2 : 0"
"2 : 0 : 1"
"2 : 1 : 0"
"3 : 0 : 0"
General algorithm
You can compute all combinations in the general case as well.
This JavaScript recursive function prints out the order of each term.
It works for any n and any number of terms nb_terms = $|\{k_1, k_2, \cdots, k_m\}|$:
// list_k : a list containing [k1, k2, ..., km]
function diophantine(n, nb_terms, k_prev, list_k){
if( nb_terms <= 1 ){
var k_terminal = n - (k_prev);
// add to tail:
list_k.push(k_terminal);
// Print result:
let str = "";
for(k of list_k ){
str = str + k + " : ";
}
console.log(str.slice(0, -3));
return;
}
for(var k = 0; k <= n-k_prev; k++ )
diophantine(n, (nb_terms-1), (k+k_prev), list_k.concat(k));
}
Running the algorithm for $k_1+k_2+k_3+k_4 = 5$ and print out solution in the console:
console.log("Diophantine: ");
diophantine(/*n=*/5, /*nb_terms*/4, 0, []);
Examples for 3 terms
Developing a few examples by hand (not necessarily from the general Leibniz rule) may help see some patterns and help you get insights (you can use software like wxMaxima to do the developments for you if you are lazy like me), this is also useful to double check your interpretation of the formula.1st order
$$ \Big(f(x) \ g(x) \ h(x)\Big)' = \begin{array}{llll} & f(x) & g(x) & h'(x) & + \\ & f(x) & g'(x)& h(x) & + \\ & f'(x)& g(x) & h(x) \end{array} $$2nd order
$$ \Big(f(x) g(x) \ h(x)\Big)'' = \begin{array}{llll} & & f(x) & g(x) & h''(x) & + \\ & & f(x) & g''(x) & h(x) & + \\ & & f''(x) & g(x) & h(x) & + \\ \\ & 2 & f(x) & g'(x) & h'(x) & + \\ & 2 & f'(x) & g(x) & h'(x) & + \\ & 2 & f'(x) & g'(x) & h(x) & + \\ \end{array} $$3rd order
$$ \Big(f(x) g(x) \ h(x)\Big)''' = \begin{array}{llll} & & f(x) & g(x) & h'''(x) & + \\ & & f(x) & g'''(x)& h(x) & + \\ & & f'''(x) & g(x) & h(x) & + \\ \\ & 3 & f(x) & g'(x) & h''(x) & + \\ & 3 & f'(x) & g''(x) & h(x) & + \\ & 3 & f''(x) & g(x) & h'(x) & + \\ \\ & 3 & f(x) & g''(x) & h'(x) & + \\ & 3 & f'(x) & g(x) & h''(x) & + \\ & 3 & f''(x) & g'(x) & h(x) & + \\ \\ & 6 & f'(x) & g'(x) & h'(x) & + \\ \end{array} $$Trinomial
Notice the correspondence with this trinomial where a power of 'zero' means we don't differentiate, a power of 'one' represent the first derivative and so on:
$$ (x + y + z)^3 = \begin{array}{llll} & x^3 & & & + \\ & & y^3 & & + \\ & & & z^3 & + \\ 3 & x^2 & y & & + \\ 3 & x^2 & & z & + \\ 3 & & y^2 & z & +\\ 3 & x & y^2 & & + \\ 3 & & y & z^2 & + \\ & x & z^2 & & + \\ 6 & x & y & z & \end{array} $$Example for 4 terms
Say you have 4 functions that you differentiate to the 2nd order $(f . g . h . i )''$. Then you want to find all the patterns that satisfy $k_1+k_2+k_3+k_4=2$ where k would be the order of differentiation, below I illustrate how orders sum together:
f g h i
--------------
f'' g h i = ''
f g'' h i = ''
f g h'' i = ''
f g h i'' = ''
f' g' h i = ''
f g' h' i = ''
f g h' i' = ''
f' g h' i = ''
f' g h i' = ''
f g' h i' = ''
Reference
- https://math.stackexchange.com/questions/3062223/sum-of-each-combination
- http://mathonline.wikidot.com/the-trinomial-theorem
- http://mathonline.wikidot.com/nonnegative-integral-solutions-to-simple-equations
Special case:
- https://en.wikipedia.org/wiki/Trinomial_expansion
- https://sahilmohnani.wordpress.com/2013/03/27/the-trinomial-theorem-and-pascals-tetrahedron/
- https://www2.edc.org/makingmath/mathprojects/pascal/Image23.gif
No comments
 Donate
Donate