How to derive the formula of the curvature of a curve
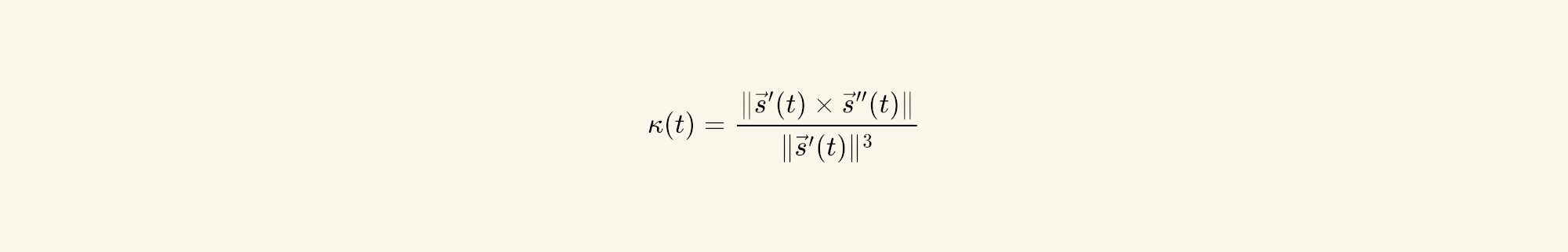
In this article we will explain and derive the following formula: let \( \s: \mathbb R \rightarrow \mathbb R^3 \) be a vector valued function representing a parametric curve \( \s(t) \) with \( t \in \mathbb R \) the curve's parameter; the curvature of \( \s\) is given by \( \kappa: \mathbb R \rightarrow \mathbb R \) as follows:
\[ \begin{equation} \kappa(t) = \frac{ \| \s'(t) \times \s''(t) \| }{ \| \s'(t) \|^3 } \label{eq:curve_3d} \end{equation} \]
Notations:
- '×' is the cross product
- \( \s'(t) \) velocity vector at \( t \)
- \( \s''(t) \) the acceleration
- \( \| \ \| \) the Euclidean norm of a vector
- dot product: \( \langle \vec a_1 \cdot \vec a_2 \rangle \)
- scalar multiplication: \( (c .\vec a) \) (parenthesis are optional)
This formula works for any parametrization of the curve, in other words, the computed curvature \(\kappa(t)\) stays the same regardless of how fast a point \(\s(t)\) travels on the curve according to its parameter \(t\).
If you don't have the formula, i.e. analytical expression of \( \s(t)\), you can numerically compute $\s'$ and $\s''$:
\[ \s'(t) = \frac{ s(t+h)-s(t-h) } {2h} \ \text{ and } \ \s''(t) = \frac{ \s'(t+h)-\s'(t-h) } {2h} \]
with \(h\) small, for instance \( h < 0.0001 \)
Code to visualize the curvature:
- 2d version: shadertoy.com/view/Mlf3zl
- 3d version: shadertoy.com/view/XlfXR4
// Under MIT License
// Copyright © 2015 Inigo Quilez
// OpenGL / GLSL shader code
// Computes the curvature of a parametric curve f(x) as
// c(f) = | f' x f''| / |f'|^3
// More info here: https://en.wikipedia.org/wiki/Curvature
vec3 a, b, c, m, n;
// parametric curve value s(t):
vec3 mapD0(float t){
return 0.25 + a*cos(t+m)*(b+c*cos(t*7.0+n));
}
// curve derivative (velocity) s'(t)
vec3 mapD1(float t){
return -7.0*a*c*cos(t+m)*sin(7.0*t+n) - a*sin(t+m)*(b+c*cos(7.0*t+n));
}
// curve second derivative (acceleration) s''(t)
vec3 mapD2(float t){
return 14.0*a*c*sin(t+m)*sin(7.0*t+n) - a*cos(t+m)*(b+c*cos(7.0*t+n)) - 49.0*a*c*cos(t+m)*cos(7.0*t+n);
}
//----------------------------------------
float curvature( float t ){
vec3 r1 = mapD1(t); // first derivative
vec3 r2 = mapD2(t); // second derivative
return length(cross(r1,r2)) / pow(length(r1),3.0);
}
float curvature_reciprocal( float t ){
vec3 r1 = mapD1(t); // first derivative
vec3 r2 = mapD2(t); // second derivative
return pow(length(r1),3.0) / length(cross(r1,r2));
}
Intuition
We define the unit tangent vector on a curve as the normalized velocity: \[ \T( t ) = \frac{ \s'(t) }{ \| \s'(t) \| } \] One way to measure the curvature \( \kappa(r) \) at parameter value \( r \in \mathbb R \) of a curve \(\s\), is to think of \(\kappa\) as the amount of deviation $\| \delta \T \|$ of the unit tangent vector \( \T \):
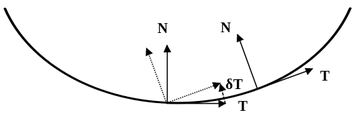
Concretely, the length of the deviation vector \(\delta \T \) defines the amount of curvature:
\[ \| \delta \T \| = \frac{ \left \| \T(r+h) - \T(r-h) \right \| }{2h} = \kappa(r) \](with \(h\) small).
For instance, with a flat curve, \( \| \delta \T \| \) is always null, since the tangent vector \(\T\) always align with itself anywhere on the straight curve.
Deriving the formula
Constant velocity
Let's consider the special case where a parametric curve \( \vec \gamma(r) \) with the parameter \(r \in \mathbb R\) has a constant speed \( \| \vec \gamma' \| = 1 \) everywhere. Notice that we use '\(r\)' to name the parameter of the curve, as we want to emphasis it represents the distance on the curve; as opposed to the time parameter '\(t\)', which indicates the velocity of a point on the curve may vary.
Now, if we want to measure the deviation of the unit tangent vector \(\T(r)\) intuitively you would want to take its derivative \(\T'(r)\), since differentiating, is the equivalent of measuring the difference \(\T(r+h) - \T(r-h)/2h\). And in this particular case, this works out fine; as one step of \(r+h\) is guaranteed to represent the same distance on the curve regardless of where we evaluate \( \vec \gamma(r) \). Therefore, the difference accurately represents the deviation rate of \(\T\) at some point 'r' of the curve.
So, constant unit velocity implies: \( \T( r ) = \frac{\vec \gamma'(r) }{ \| \vec \gamma'(r) \| = 1} = \vec \gamma'(r) \), which naturally leads to \( \T'( r ) = \vec \gamma''(r) \). Here, the length of the acceleration of \( \vec \gamma \) represents the curvature:
$$ \kappa(r) = \| \vec \gamma '' (r) \| \rlap{\annotation{ \text{ if and only if } \| \vec \gamma' \| = 1 \\ \text{ anywhere on the curve } } } $$Let's reformulate one more time this result: as can be shown mathematically, constant speed implies the acceleration vector is always orthogonal to the velocity vector! This is really handy, since in this case, acceleration represents the amount of deviation of the velocity. So to compute the curvature \(\kappa\) we only need to derivate \(\gamma\) twice.
Arc-length parametrization
Let's understand where the more general formula \( \kappa(t) = \frac{ \left \| \s'\times \s''\right\|}{\|\s'\|^3} \) comes from, and how to derive it. The journey is long but worth it. Among other things, this is a really good training to manipulate vector expressions, do advanced calculus and algebraic manipulation.
Time parametrization vs arc-length parametrization
When a curve has constant velocity, we say that it is parametrized according to the "arc-length". This so called "arc-length" is defined as the distance between two points along a section of a curve. In other words, in "arc-length" parametrization, the distance traveled along the curve is the same everywhere regardless of the parameter's value \(t\), or more precisely, increments of the curve's parameter \(t\) should be proportional to the arc-length distance \( r \). For instance, the distance between \(\gamma(t)\) and \( \gamma(t+h) \) on the curve, should be consistently the same, whether we measure it at \(t= 0.1\) or \(t=0.6\) etc.
In the general case, the velocity of a curve \( \s(t) \) may not equal to 1.
Below we illustrate the travel of two points \(A\) and \(B\)
along two identical parametric lines, but with different parametrization:
\(A = x_{start}.(1-t) + x_{stop}.t\)
\(B = x_{start}.(1-t^2) + x_{stop}.t^2\)
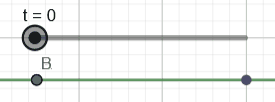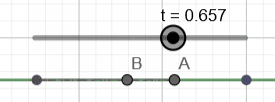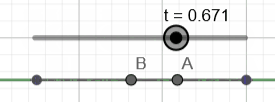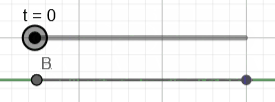
While \(A\) travels at constant speed, clearly \(B\) accelerates and decelerates, which implies a curvature defined as \( \kappa(t) = \|\s''(t) \|\) is not always null, an obvious contradiction since straight lines should have null curvature everywhere.
Warning: although differences of \( \T( t ) = \s'(t) / \| \s'(t) \| \) would work for the particular case of a straight line even for a general parametrization \( \| \s' \| \neq 1 \) (since subtracting the normalized velocity will return a null vector), this does not apply to other types of curves. What we truly need is \(\T( r )\)
Remark 1: usually a curve is denoted \( \vec \gamma \) when parametrized according to the arc-length.
Remark 2: Whether the curvature formula is expressed in terms of '$t$' or '$r$' generally yields different results. By different we mean that if you set \(t = r\) then most of the time \(\kappa(t) \neq \kappa(r)\). Why? They should both measure the same curvature right? Yes, but it does not measure it at the same position of the curve! \(\s(t)\) and \(\s(r)\) may not return the same point on the curve, hence, curvature is, in general, not the same. Both \(\kappa(t) \) and \( \kappa(r)\) return the same curvature only if evaluated for the same position, which usually implies \(t \neq r\), unless '$t$' and '$r$' represents the same parametrization.
Deviation of \( \T \) according to arc-length
To find the curvature in the general case, where the curve has a general parametrization with possibly \( \|\s' \| \neq 1 \), we need to find the deviation of the unit tangent vector \( \T \) according to the arc-length! (as opposed to time)
First, we present the result. But for things to really sink in,
let's rephrase one more time:
the parameter \(t\) of \( \T(t) \) does not necessarily represents the arc-length;
to measure the deviation of \( \T(t) \), instead of taking the derivative \( \T'(t) \) with respect to time,
which would give you how fast the tangent vector \( \T \) is changing with respect to time,
we're looking at the rate of change with respect to the distance \( r \) on the curve:
\[ \kappa(r) = \left\| \frac{ \d\T }{ \d r }\right \| \]
Later we'll demonstrate it implies: \[ \kappa(t) = \frac{ \|\T'(t)\| }{ \|s'(t)\| } \]
Having the curvature \(\kappa(t)\) expressed in terms of the time \(t\) and \( \T'(t) \) instead of the arc-length \( \T'(r) \), gets us one step closer to the final formulation \(\kappa(t) = { \left \| \s'(t) \times \s''(t) \right\|} / {\|\s'(t)\|^3}\).
Homework
This paragraph presents exercises to manipulate and get familiar with the above formula, and is not necessary for the rest of the demonstration.
Before doing any demonstration, let's numerically check that \(\frac{ \|\T'(t)\| }{ \|s'(t)\| } \) yields the same results as \(\kappa(t) = \frac{ \left \| \s'(t)\times \s''(t)\right\|}{\|\s'(t)\|^3}\)
// This code is an excerpt from:
// https://www.shadertoy.com/view/csc3Dj
// We check that the analytical solution:
// k(t) = | s(t)' x s(t)''| / |s(t)'|^3
// Is equivalent to a numerical solution such as:
// k(t) = ||T'(t) || / || s'(t) ||
// Should return a constant value if the two formula are equivalent:
float curvature( float t ){
return curvature_analytical( t ) - curvature_numerical( t );
//return 1.0/curvature_analytical( t );
//return 1.0/curvature_numerical( t );
}
// k(t) = | s(t)' x s(t)''| / |s(t)'|^3
float curvature_analytical( float t )
{
vec2 r1 = mapD1(t); // first derivative
vec2 r2 = mapD2(t); // second derivative
return length(cross2d(r1,r2)) / pow(length(r1),3.0);
}
// k(t) = ||T'(t) || / || s'(t) ||
float curvature_numerical( float t )
{
vec2 acc = diff_tangent(t);
float speed = length(mapD1(t)); // || s'(t) ||
float kappa = length(acc) / speed;
return kappa;
}
// return T(t)
vec2 tangent(float t){
vec2 r1 = mapD1(t); // first derivative i.e curve's velocity
return r1 / length(r1);
}
// return T'(t)
// (First order accuracy)
vec2 diff_tangent2(float t){
float h = 0.0001;
return (tangent(t+h*0.5) - tangent(t-h*0.5)) / h;
}
// return T'(t)
// (Second order accuracy -2,-1,0,1,2 )
// https://web.media.mit.edu/~crtaylor/calculator.html
vec2 diff_tangent3(float t){
float h = 0.0001;
return (tangent(t-2.0*h) - 8.0*tangent(t-h) + 8.0*tangent(t+h) - tangent(t+2.0*h) ) / (12.0*h);
}
// return T'(t)
// 8th order accuracy -4,-3,-2,-1,0,1,2,3,4
// https://web.media.mit.edu/~crtaylor/calculator.html
vec2 diff_tangent(float t){
float h = 0.0001;
return (
3.0*tangent(t-4.0*h)
-32.0*tangent(t-3.0*h)
+168.0*tangent(t-2.0*h)
-672.0*tangent(t-h)
+672.0*tangent(t+h)
-168.0*tangent(t+2.0*h)
+ 32.0*tangent(t+3.0*h)
- 3.0*tangent(t+4.0*h)
) / (840.0*h);
}
You can also check the formula are equivalent on a simple analytical expression as well:
Consider the curve: \[\s \left( t \right) = \left\langle {t, \ 3 \sin(t), \ 3 \cos(t) } \right\rangle\]
Let's compute its curvature with: \[\kappa(t) = \frac{ \|\T'(t)\| }{ \|s'(t)\| } \]
Velocity is found by deriving x, y and z components of \( \s(t)\): \[ \s'\left( t \right) = \left\langle {1,3\cos(t), - 3\sin(t)} \right\rangle \]
Taking the norm requires to use a trigonometric identity: \[ \begin{align*} \left\| {\s'\left( t \right)} \right\| & = \sqrt {(1)^2 + (3 \cos(t))^2 + (3\sin(t))^2 } \\ & = \sqrt {1 + 9{{\cos }^2}t + 9{{\sin }^2}t} \\ & = \sqrt {1 + 9 ( \cos^2(t) + \sin^2(t)) } \annotation{ \text{Pythagorean identity } \\ \cos^2(t) + \sin^2(t) = 1 } \\ &= \sqrt {10} \\ \end{align*} \]
By definition the tangent is the normalized velocity: \[ \begin{align*} \T\left( t \right) &= \frac{ \s'(t) }{ \| \s'(t) \| } \\ &= \left\langle {\frac{1}{{\sqrt {10} }},\frac{3}{{\sqrt {10} }}\cos( t ), - \frac{3}{{\sqrt {10} }}\sin( t )} \right\rangle \end{align*} \]
The first derivative of the tangent: \[ \begin{aligned} \T'( t ) &= \bigg \langle \frac{1}{\sqrt 10} & ,& \phantom{-} \frac{3}{\sqrt 10 } \cos( t ) & ,& - \frac{3}{ \sqrt 10 } \sin( t ) \bigg \rangle' \\ &= \bigg \langle 0 & ,& -\frac{3}{\sqrt {10} } \sin( t ) & ,& - \frac{3}{ \sqrt {10} } \cos( t ) \bigg \rangle \\ \end{aligned} \]
Taking its norm:
\[ \begin{align*} \left\| {\T'\left( t \right)} \right\| & = \sqrt {0 + \frac{9}{{10}}{{\sin }^2}t + \frac{9}{{10}}{{\cos }^2}t} \\ &= \sqrt {\frac{9}{10} \times 1 } \annotation{ \text{Pythagorean identity } \\ \cos^2(t) + \sin^2(t) = 1 } \\ &= \frac{3}{{\sqrt {10} }} \end{align*} \]
Here we go, the curvature is: \[ \kappa(t) = \frac{{\left\| {\vec T'\left( t \right)} \right\|}}{{\left\| {\vec s'\left( t \right)} \right\|}} = \frac{{{}^{3}/{}_{{\sqrt {10} }}}}{{\sqrt {10} }} = \frac{3}{{10}} \]
Now let's do the same with:
\[ \kappa(t) = \frac{ \left \| \s'(t)\times \s''(t)\right\|}{\|\s'(t)\|^3} \]We need the acceleration: \[ \begin{aligned} \s' \left( t \right) & = \langle 1 , & \phantom{-} 3\cos(t) &,& - 3\sin(t) \rangle \\ \s''\left( t \right) & = \langle 0 , & -3\sin(t) &,& - 3\cos(t) \rangle \\ \end{aligned} \]
Instead of doing it by hand, let's have fun and do the rest of the development using WxMaxima
% load(vect); /* to work with vectors we need that package loaded */ % declare(express, evfun); /* allows express() to be used inside ev() */ % s(t) := [1, 3*cos(t), -3*sin(t) ]; /*s'(t)*/ % ss(t) := diff(s(t), t); /* s''(t) */ /* express() is needed to develop the cross product operator '~' */ /* we also have to explicitly write ev() when using with ':=' assignement otherwise it tries to evaluate the whole assignement 's_cross_ss(t) := ev(s(t)~ss(t)'*/ % s_cross_ss(t) := ev(s(t)~ss(t), express, factor, trigreduce); /* s' x s'' */ % norm_s_X_ss : sqrt( s_cross_ss(t).s_cross_ss(t) ), factor, trigreduce; /* | s' x s'' | */ % cubed_norm : sqrt( s(t).s(t) )^3, expand, trigreduce; /* |s'|^3 */ % (norm_s_X_ss / cubed_norm); /* curvature ! */
Maxima will find back the same curvature value: \[ \kappa(t) = \frac{ \left \| \s'(t)\times \s''(t)\right\|}{\|\s'(t)\|^3} = \frac{3}{{10}} \]
Re-parametrize \(\s\) according to arc-length
Since \(\T\) is originally computed based on the curve parametrized according to time \(\T( t ) = \s'(t) / \| \s'(t) \|\) we need to re-parametrize the curve \(\s(t)\) according to the arc-length, i.e. \(\s(r)\), in order to get \(\T(r)\). To this end, we use an intermediate function \( r(t): \mathbb R \rightarrow \mathbb R \) which maps \(t\) to the distance on the curve, we define it as follows:
$$ \begin{equation} \begin{aligned} r(t) & = \int_a^t \| \s'(u) \| \text{d}u \\ \Rightarrow r'(t) & = \| \s'(t) \| \annotation{\text{The fundamental theorem of calculus } \\ \text{tells us to replace } u \text{ by the upper bound } t} \end{aligned} \label{arc_len_map} \end{equation} $$
Proof of the arc length formula
Alternate video explanation
The above formula defines \(r(t)\) as the distance from the start of the curve to some parameter value \(t\). The inverse function of \(r(t)\) is \( t(r) \), which fortunately, we won't have to derive.
\[ \begin{array}{lllllllll} r(t) : & \{ \text{time} & \in \mathbb R \} & \longmapsto & \{ \text{arc-len} & \in \mathbb R \} \\ t(r) : & \{ \text{arc-len} & \in \mathbb R \} & \longmapsto & \{ \text{time} & \in \mathbb R \} \end{array} \]
Keep in mind that in the general case \( \kappa(t) \neq \kappa(r) \). The curvature \(\kappa(t) \) or \(\kappa(r)\) are only the same when '$t$' and '$r$' are chosen to evaluate the same point on the curve: \[ \kappa(t(r)) = \kappa(r) \] \[ \kappa(r(t)) = \kappa(t) \]
Now, the arc-length re-parametrization of the curve is simply \( \s(t(r)) = \vec \gamma(r)\). An important fact we will use below: the first derivative \( \vec \gamma'(r)\) is a unit tangent vector, since by definition a curve parametrized according to the arc-length has a speed of 1 everywhere. Which leads to notice it does not really matter how we parametrize the unit tangent:
$$ \T(t) = \T(t(r)) \Annotation{\text{assuming we choose an } r \text{ such as:} \\ t = t(r) } $$Keeping all the above in mind let's develop \(\frac{ \d \T}{\d r}\):
$$ \begin{aligned} \frac{ \d \T}{\d r} &= \frac{ \d \T \big(t(r)\big)}{\d r} \\ &= \Big [ \T \big(t(r)\big) \Big ]' \annotation{ \text{alternate notation} } \\ &= \T'\big (t(r) \big) \ . \ t'(r) \annotation{ \text{chain rule} } \\ &= \T'(t(r)){ {\d t} \over {\d r} } \end{aligned} $$The curvature is the length of this vector:
$$ \begin{aligned} \kappa(\red{r}) & = \left \| {\bf T}'(t(r)) { {\d t} \over {\d r} } \right \| \\ \end{aligned} $$
The next step of the development from here may be confusing to some⚠️. What we are going to do is to stop evaluating at '$r$' the curvature and evaluate everything directly at '$t$' instead. Doing so, we loose the arc-length parametrization, in the sens that, \( \kappa(t) \) will now return the curvature at \( \s(t) \) where '$t$' is not guaranteed to be proportional to the distance on the curve. Nonetheless, since we are developing from \(\T / \d r\), our curvature \( \kappa(t) \) still captures the variations of \(\T\) according to the arc-length. To achieve this, we need the "inverse function theorem":
$$ \begin{aligned} \kappa( \red{t}) & = \left \| \frac{ {\bf T}'(t) }{ \d r / \d t } \right \| \annotation{\text{a) } \href{/?e=149}{\underline{\text{inverse function theorem }}} \d t / \d r = \frac{1}{\d r / \d t } \\ \text{b) evaluate directly in } t \text{: } \T(t)=\T(t(r))\\ \text{(More details afterwards)} } \\ & = \left \| \frac{ {\bf T}'(t) }{{r}'(t)} \right \| \\ & = \left \| \frac{ {\bf T}'(t) }{\|{\s}'(t)\|} \right \| \annotation{ \text{by definition of the arc-length as shown in \eqref{arc_len_map}} }\\ & = \frac{ \| {\bf T}'(t) \|}{\|{\s}'(t)\|} \annotation{ \text{scaling inside or outside the norm is the same} } \\ \end{aligned} $$
Those not familiar with the inverse function theorem might see the following as black magic:
\[ \d t / \d r = \frac{1}{\d r / \d t }\]We can find back this result using the chain rule: \[ \begin{aligned} t \big ( r(t) \big) & = t \annotation{ \text{by definition of an inverse function}} \\ \Big( t \big (r(t) \big ) \Big)' & = \Big ( t \Big)' \\ t' \big(r(t)\big) . r'(t) & = 1 \\ t' \big(r(t)\big) & = \frac{1}{r'(t)} \\ t' (r) & = \frac{1}{r'(t(r))} \\ \end{aligned} \] The magic 🧙🪄 lies in the fact that if we choose to evaluate in \(t\) we don't need to know \(t\) and can deduce \(t'\) solely in terms of \(r'\) !!
Ref 1: Here is an alternate article explaining a similar derivation
that leads to dividing by \(\|{\s}'(t)\|\)
Ref 2: My article on the visual interpretation of the inverse theorem.
Ref 3: Video on the inverse function theorem.
Alternate derivation of $\kappa(t)$
The why:
This is not a mandatory step, since we just derive the same things as the above but using an alternate approach.
Here we analyze Micheal Penn's derivation.
So what follows in this section is not necessary to comprehend the next section, however, I still recommend the read.
This is a really good exercise to read advanced notations and understand other complex mathematical developments out there.
In particular, I show how the Leibniz notation can hide the inverse function theorem,
as well as a lesser known version of the chain rule. So if you want to step up your algebraic development skills, follow along.
The what: (original transcript)
First, here is a transcript of the proof. It uses notations I don't really like.
It lacks variable names, this doesn't feel rigorous as it may leave space to interpretation errors.
Anyhow, the proof begins with some definitions:
Notice the lack of variable in $\T$; this may be confusing because we started with $\kappa(t)$ and not $\kappa(r)$, however, $\d r$ indicates we derive according to '$r$'. So this necessarily means a function composition is hidden to do the re-parametrization of $\T(?)$. Try to guess if $?=r(t)$ or $?=t(r)$ and keep reading. But let's move on:
\[ \T = \frac{s'}{\|s'\|} \]I'm less bothered omitting variables in the above, it simply means any parametrization works to find the tangent, this will only change the location of the tangent on the curve. Now, onto the proof:
\[ \begin{aligned} \T' &= \frac{\d\T }{ \d t} \\ &= \frac{\d \T }{ \d r} . \frac{\d r }{\d t} \annotation{\text{Mr. Penn says "we apply the chain rule" }\\ \text{(we will see this is a trap)}} \\ &= \frac{\d \T }{ \d r} . \| \vec s'(t) \| \end{aligned} \]Divide both sides by \(\| \vec s'(t) \|\)
\[ \frac{\d \T }{ \d r} = \frac{\T' }{ \| \vec s'(t) \|} \Rightarrow \kappa = \frac{\| \T' \| }{ \| \vec s' \|} \] The issue:Ok, here is where things get hairy. Looking at this proof at first, every step may make a lot of sens, however, notice the final answer $\kappa = \frac{\| \T' \| }{ \| \vec s' \|}$ lacks any explicit mention of $t$. What if, we want to make sure this development leads indeed to the curvature according to any parametrization? Or if we want to check we haven't missed anything ignoring the underlying variables. Well, trying to explicitly write down every variables will reveal more intricacies and is not so easy (trying this before reading may be a good exercise).
The anwser:Let's end this cliff hanger, the treacherous part is right here:
$$\frac{\d\T }{ \d t} = \frac{\d \T }{ \d r} . \frac{\d r }{\d t}$$Mr. Penn says we use the chain rule, so you may be inclined to interpret it as the traditional formula $\Big(f(g(x)) \Big)' = f'(g(x)) . g'(x)$ in our case:
$$ \Big[ \T \big ( r(t) \big ) \Big ] ' = \T' \big (r(t) \big ) . r'(t)$$which would be... completely wrong! If you continue developing from there, this will lead nowhere, and certainly not to $\frac{ \| \T'(t) \|}{\| \s'(t) \|}$. Actually you may be stuck with a $\frac{ \| \T'(r(t)) \|}{\| \s'(t) \|}$ if you follow that path.
So what's going on? Well we are supposed to parametrize $ \T $ with $t(r)$. This is actually the only parametrization that makes sens for what we are trying to achieve. Hopefully you answered correctly to the previous question about $\T(?)$ or at least you now see why this is a requirement to properly compute the curvature.
That being said, we need to re-organize the traditional chain rule for this to make any sens:
\[ \begin{aligned} \Big(f(g(x)) \Big)' &= f'(g(x)) . g'(x) \annotation{\text{ traditional chain rule } } \\ f'(g(x)) &= \Big(f(g(x)) \Big)' . \frac{1}{g'(x)} \annotation{\text{ divide by } g' } \\ f'(g(x)) &= \Big(f(g(x)) \Big)' . {g^{-1}}'(y) \annotation{\text{the inverse function theorem tells us: }\\ 1/g'(x) = {g^{-1}}'(y) } \end{aligned} \]In the case that interests us, this means:
$$ \frac{\d \T }{ \d t} = \frac{\d \T }{ \d r} . \frac{\d r }{\d t} \\ \Leftrightarrow \\ \frac{\d \T \big ( t(r) \big ) }{ \d t} = \frac{\d \T \big(t(r)\big) }{ \d r} . \frac{\d r(t) }{\d t} \\ \Leftrightarrow \\ \T'\big (t(r)\big) = \Big(\T(t(r)) \Big)' . r'(t) $$So this is neat or hell depending on your inclination😅. You can see this as an alternate chain rule applied onto the inner variable $\T'\big ( \red{t}(r)\big)$ with the added bonus that it adds the inverse function theorem in the mix. This explains the hack in Leibniz notation $\frac{\d \T }{ \red{ \d r } } . \frac{ \red{ \d r } }{\d t}$ where we multiply by $\d r / \d r$. The notational trick helps reduce your cognitive load, but you have better keep in mind what function composition are involved.
Now let's wrap this up and do a final check. We explicitly name all variables while we go deep into the details of the development:
\[ \begin{aligned} \T'\big (t(r) \big ) & = \frac{ \d \ \T \big ( t(r) \big ) }{\d t} \\ & = \frac{ \d \ \T \big ( t(r) \big ) }{\red{ \d r} } . \frac{ \red{\d r} }{\d t} \annotation{\text{"chain rule" + inverse function theorem}} \\ & = \frac{ \d \ \T \big ( t(r) \big ) }{\d r} . \frac{\red{ \d } }{\d t} \red{ \int_a^t \| \s'(u) \| \d u } \annotation{ \text{as shown in \eqref{arc_len_map}} } \\ & = \frac{ \d \ \T \big ( t(r) \big ) }{\d r} . \red{ \| \s'(t) \| } \annotation{\text{Fundamental theorem of calculus}} \\ \frac{\T'\big (t(r) \big )}{ \red{ \| \s'(t) \| } } & = \frac{ \d \ \T \big ( t(r) \big ) }{\d r} \annotation{\text{divide by } \| \s'(t) \|}\\ \underbrace{\frac{\d \ \T \big ( t(r) \big ) }{\d r}}_{\text{deviation of }\T \text{ according } \\ \text{to the arc-length} } & = \frac{\T'\big (t(r) \big )}{\| \s'(t) \|} \annotation{\text{invert left and right hand side} }\\ & \\ \left \| \frac{\d \ \T}{\d r} \right \| & = \left \| \frac{\d \ \T \big (t(r) \big ) }{\d t} . \frac{1}{\| \s'(t(r)) \|} \right \| \annotation{ \text{apply norm to both sides.}\\ \text{re-organize, change notations.} \\ t(r) \text{ is unknown, but that's ok.}} \\ & = \frac{ \left \| \T'(t(r)) \right \|}{\| \s'(t(r)) \|} \\ \kappa(t) & = \frac{ \| \T'(t) \|}{\| \s'(t) \|} \annotation{\text{Evaluate directly in } t} \\ \end{aligned} \]Raw development
Alright, so far we derived a formula for the curvature that can be evaluated for any curve parametrization \(\s(t)\):
\[ \kappa(t) = \frac{ \| \T'(t) \|}{\| \s'(t) \|}\]The issue with the above is that we can't evaluate \(\kappa(t)\) solely in terms of \(\s\) or its derivatives \(\s'\), \(\s''\) etc. for this we need to explicitly differentiate \(\T'(t)\) to find a nice closed formed expression. Our goal is to find back:
\[\kappa(t) = \frac{ \| \s'(t) \times \s''(t) \| }{ \| \s'(t) \|^3 }\]There are many ways to derive the formula of the curvature, this is just one of them. Arguably not the most elegant approach, however, I find it somewhat easier to grasp and read. In this approach, we can unroll our reasoning and algebraic developments almost in a linear fashion. Note that, this demonstration stems from a very condensed version presented here.
Outline: We start by computing and expanding the expression of \( \T'(t)\) then move on finding \( \| \T'(t) \|^2 \) to finally get to \( \| \T'(t) \|\) and \( \frac{\| \T'(t) \|}{ \| \s'(t) \|}\).
Notations:
- dot product: \( \langle \vec a_1 \cdot \vec a_2 \rangle \)
- scalar multiplication: \( (c .\vec a) \) (parenthesis are optional)
$$ \begin{align*} \underset{\mathbb R \rightarrow \mathbb R^3 }{ \left ( \T(t) \right )' } = \left(\frac{ \vec s'(t)}{ \| \vec s'(t) \| }\right)' & = \frac{ \s'' . \| \s' \| - \s' . (\| \s' \|)' }{ \| \s' \|^2 } \annotation{(u.v)' = (u'.v - u.v') / v^2 } \\ & = \frac{ \s'' . \| \s' \| - \s' . \red{ \dotprod{ \nabla[\| \s' \|] }{ \s'' } } }{ \| \s' \|^2 } \annotation{ f : \mathbb R^n \rightarrow \mathbb R; (f(\vec a))' = \nabla f(\vec a) . \vec a' \ \ \href{?e=62#chainRule_vectorFun-In-ScalarField}{\underline{\text{chain rule}}} \\ \text{In our case: } f = \| \| } \\ & = \frac{ \s'' . \| \s' \| - \s' . \dotprod{ \red{\frac{\s'}{ \| \s' \| }} }{ \s'' } }{ \| \s' \|^2 } \annotation{ \| \|: \mathbb R^n \rightarrow \mathbb R; \nabla [ \| \vec {x} \| ] = \frac{ \vec {x}}{ \| \vec {x} \|} \ \ \href{?e=62#gradient-of-the-norm}{\underline{\text{gradient of the norm}}} } \\ & = \frac{ \s'' . \| \s' \|}{ \red{\| \s' \|^2} } - \frac{ \s' . \dotprod{ \frac{\s'}{ \| \s' \| } }{ \s'' } }{ \red{\| \s' \|^2} } \annotation{\text{Distribute division}} \\ & = \frac{ \s'' . \| \s' \| }{\| \s' \|^2} - {\s' . \frac{ \dotprod{\s'}{\s''} }{ \red{ \| \s' \|^3} } } \annotation{\text{Dot product is homogeneous under scaling} \\ \dotprod{\alpha . \vec a}{ \vec b} = \alpha . \dotprod{\vec a}{ \vec b} } \\ &= \frac{ \s'' . \| \s' \|^{\red{2}} }{\| \s' \|^{\red{3}}} - \frac{\s' . \dotprod{\s'}{\s''}}{ \| \s' \|^3 } \Annotation{ \tag{res1} \label{eq:res1} } \end{align*} $$
Now we need to work our way to \(\| \T'\|^2\) to further develop towards an expression that make use of the dot product. First, we need to pause our current development, and demonstrate a few intermediate properties.
(I) \( \T \) is the unit tangent, thus by definition its norm is constant \( \| \T \| = 1 \). From this fact alone, we can demonstrate \( \dotprod{\T}{\T'} = 0\) (i.e. \( \T \perp \T'\)).
In the general case, these 3 expressions are equivalent:
$$ \Leftrightarrow \left . \begin{matrix} \| \vec u \| & = & c \\ \| \vec u \|^2 & = & c \\ \dotprod{\vec u}{\vec u} & = & c \\ \end{matrix} \right . $$
Now, differentiate the dot product of \(u(t)\) over itself, and watch the magic happen: $$ \begin{aligned} \dotprod{ u(t) }{ u(t) }' & = (c)' \\ \dotprod{ u'(t)}{ u(t) } + \dotprod{ u(t) }{ u'(t) } & = 0 \annotation{\text{apply dot product rule}} \\ 2\dotprod{u'}{u} & = 0 \\ \dotprod{u'}{u} & = 0 \annotation{\text{which means} \ u' \perp u }\\ \end{aligned} $$
(II) It follows that: \(\dotprod{\T'}{\s'} = 0\), since:
$$ \begin{aligned} \dotprod{\T}{\T'} & = 0 \\ \dotprod{\frac{\s'}{ \|\s'\| }}{\T'} & = 0 \annotation{\T = \s' / \| \s' \| \quad \text{by definition}}\\ \dotprod{\s'}{\T'} & = 0 \end{aligned} $$
(III) Finally, let's prove that \( \|\T'\|^2 = \dotprod{\T' }{ \frac{\s''}{\|\s'\|} } \) by developing $\eqref{eq:res1}$ :
$$ \begin{align*} \T' & = \frac{ \s'' . \| \s' \|^2 }{\| \s' \|^3} - \frac{\s' . \dotprod{\s'}{\s''}}{ \| \s' \|^3 } \\ \dotprod{\T'}{ \red{\T'}} & = \dotprod{ \left ( \frac{ \s'' . \| \s' \|^2 }{\| \s' \|^3} - \frac{\s' . \dotprod{\s'}{\s''}}{ \| \s' \|^3 } \right ) } { \red{\T'} } \\ \dotprod{\T'}{\T'} & = \frac{ \dotprod{\s''}{ \red{\T'} } \| \s' \|^2 }{\| \s' \|^3} - \frac{ \overbrace{ \dotprod{\s'} {\red{\T'}} }^{0} . \dotprod{\s' }{ \s'' }}{ \| \s' \|^3 } \\ \|\T'\|^2 & = \frac{ (\s'' \cdot \T') \| \s' \|^2 }{\| \s' \|^3} \\ \|\T'\|^2 & = \frac{ (\s'' \cdot \T') }{\red{ \| \s' \|} } \\ \end{align*} $$
At last, we can resume our development. Let's apply \(\frac{\s''}{\|\s'\|}\) to the right hand side of $\eqref{eq:res1}$, since we learned this is one way to compute \(\|\T'\|^2\),
$$ \begin{align*} \|\T'\|^2 &=\dotprod{ \left( \frac{ \s'' . \| \s' \|^{2} }{\| \s' \|^{3}} - \frac{\s' . \dotprod{\s'}{\s''}}{ \| \s' \|^3 } \right)}{ \red{ \frac{\s''}{\|\s'\|}} }\\ % &=\frac{\left ( \s'' \red{\dotprod{\s'}{\s'}} - \s' \dotprod{\s'}{\s''} \right )}{\|\s'\|^3}\cdot\frac{\s''}{\|\s'\|}\\ % &=\frac{\left ( \s''(\s'\cdot \s')-\s'(\s'\cdot \s'') \right )}{\|\s'\|^3}\cdot\frac{\s''}{\|\s'\|}\\ &=\frac{\left ( \s''\|\s'\|^2-\s' (\s'\cdot \s'') \right ) }{ \red{\|\s'\|^3} }\cdot\frac{\s''}{\|\s'\|}\\ &=\frac{\red{\|\s''\|^2}\|\s'\|^2 - \dotprod{\s'}{ \s''} . \dotprod{ \s' }{ \s''}}{\|\s'\|^{\red{4}}}\\ &=\frac{\|\s''\|^2\|\s'\|^2-\red{\dotprod{\s'}{ \s''}^2}}{\|\s'\|^4}\\ &=\frac{\|\s''\|^2\|\s'\|^2-(\red{\|\s''\|\|\s'\|\cos(\theta)})^2}{\|\s'\|^4}\\ &=\frac{\|\s''\|^2\|\s'\|^2-\|\s''\|^{\red{2}}\|\s'\|^{\red{2}}\cos^{\red{2}}(\theta) }{\|\s'\|^4}\\ &=\frac{\|\s''\|^2\|\s'\|^2\left(1-\cos^2(\theta)\right)}{\|\s'\|^4} \annotation{ \text{factorize by } \|\s''\|^2\|\s'\|^2 } \\ &=\frac{\|\s''\|^2\|\s'\|^2 \red{\sin^2(\theta)}}{\|\s'\|^4} \annotation{ 1-\cos^2(\theta) = \sin^2(\theta) \ \ \href{https://en.wikipedia.org/wiki/Pythagorean_trigonometric_identity}{\underline{\text{pythagorean identity}}} } \\ &=\frac{ \big (\|\s''\| \|\s'\|\sin(\theta) \big )^{\red{2}}}{\|\s'\|^4}\\ &=\frac{ \red{ \| \s'\times \s''\|^2} }{\|\s'\|^4} \annotation{\text{we recognized the norm of the cross product}}\\ &=\frac{ \left(\| \s'\times \s''\|\right)^{\red{2}}}{ \left(\|\s'\|^2 \right )^{\red{2}}}\\ &= \left (\frac{ \| \s'\times \s''\|}{\|\s'\|^2} \right )^\red{2}\\ &= \left ( \left\| \frac{ \s'\times \s''}{\|\s'\|^2}\right \| \right )^2\\ \|\T'\|^2 &=\left\|\frac{\s'\times \s''}{\|\s'\|^2}\right\|^2 \\ & \text{And at long last, we square out both sides: } \\ \|\T'\| &= \left\|\frac{\s'\times \s''}{\|\s'\|^2}\right\| \\ & \text{Divide by velocity to enforce arc-length parametrization: } \\ \kappa(t) &= \frac{\|\T'\|}{ \red{\|\s'\|}} = \left\|\frac{\s'\times \s''}{\|\s'\|^\red{3}}\right\| \\ \kappa(t) &= \frac{\|\T'\|}{\|\s'\|} = \frac{ \left \| \s'\times \s''\right\|}{\|\s'\|^3} \end{align*} $$
Going further:
Alternate derivation of the cross product formulation of the curvature in video with Jonathan Walters:
https://www.youtube.com/watch?v=3RYeF5twUqk
Another detailed demonstration of the curvature formula:
Faculty of Khan: Arc Length and Reparameterization
Faculty of Khan: Curvature: Intuition and Derivation
Multidimensional case:
So far we developed a formula of the curvature for the 2d and 3d case, to handle any dimensions we need to rely on the multidimensional formula:
\[ \begin{equation} \kappa(t)=\frac{\sqrt{\|\gamma’(t)\|^2 \|\gamma’’(t)\|^2 - (\gamma’(t)\cdot\gamma’’(t))^2}}{\|\gamma’(t)\|^3} \label{eq:curve_nd} \end{equation} \]Developing \( \eqref{eq:curve_3d} \) and \( \eqref{eq:curve_nd} \) should show the two expressions are indeed equivalent.
More on the topic below:
Not very detailed proof of the multidimensional case
Another explanation of the multidimensional case
Related
- High level overview good to start but shallow:
- Micheal Penn Series on: multivariable calculus and curvature (lots of proofs but sometimes lacks details)
- Paul's note on vector calculus
No comments
 Donate
Donate