Definition of a Positive Definite Matrix
Literal definition
A Positive Definite matrix is a symmetric matrix \(M\) whose every eigenvalue is strictly positive.
note
So you need to know about eigen values and eigen vectors. I recommend the series Essence of Linear Algebra by 3blue1brown on the topic.
Formal definition
Formally we say a matrix \(M \in \mathbb R^{n \times n}\) is positive definite if \( \boldsymbol v^T M \boldsymbol v > 0\) for every real vector \(\boldsymbol v \in \mathbb R^n\).
Side note: a semiefinite positive matrix respects \( \boldsymbol v^T M \boldsymbol v \ge 0\) (eigen values can be null). Likewise, a Negative Definite matrix has strictly negative eigen values and so on.
Geometric interpretation
Geometrically \(\boldsymbol v' = M. \boldsymbol v\) is the transformation of the vector \(\boldsymbol v\) by the matrix \(M\). And \(\boldsymbol v^T .\boldsymbol v'\) the dot product between the vector \(\boldsymbol v\) and its transformed version. So if we have \(\boldsymbol v^T . \boldsymbol v' > 0\) this means the angle between those two vectors must be always greater than \(\pi / 2\).
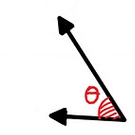
Why is that? Well recall the dot product is \(\boldsymbol a. \boldsymbol b = \|\boldsymbol a\|\|\boldsymbol b\|cos(\boldsymbol a \angle \boldsymbol b)\)
Link to eigen values
The definition of the Eigen values is: \(Mv = \lambda v\)
So if we plug some eigen vector in \( \boldsymbol v^T M \boldsymbol v \):
\(\begin{aligned} v^TMv &= v^T \lambda v \\ &= \lambda v^T \ . \ v \\ &= \lambda \| v \|^2 \end{aligned}\)In other words, if \( \boldsymbol v^T M \boldsymbol v > 0\) then \(\lambda\) must be positive since \(\| v \|^2 \) is always positive.
Caveat
We are yet to show that this is true for any vectors, not just eigen vectors. Informally, we can extend our interpretation: by definition \(M\) must be symmetric, so their exists an eigen basis we can use to express any other vectors. If we plug in our above development, a general vector expressed as a linear combination of eigen values and eigen vectors, we will come to the same conclusion that eigen values must be positives.
Some applications
1)
Analogous to real numbers where, when you multiply positive numbers together, the result doesn’t change sign.
Having a positive definite matrix means you can apply it to vectors many times while keeping the resulting vector "positive" (in a very loose kind of sens, since its more preserving a relativly similar direction inbetween multiplication).
2)
If the Hessian matrix of a multivariate function is a Positive Definite Matrix, then the function is convex.
By the way, when studying the minimum or maximum of a univariate function, we can check the sign of the second derivative (negative sign means max, and positive sign means min). The equivalent of this in multivariate calculus is the Hessian matrix.
If the Hessian is positive definite, it’s a minimum. If the Hessian is negative definite \( \boldsymbol v^T M \boldsymbol v < 0\), it’s a maximum.
Alternate tests
There are many ways to test for positive definiteness:
- All Eigen values > 0
- The quadratic energy $\boldsymbol v^T M \boldsymbol v$ is > 0
- If you can do a Cholesky decomposition $S = A^T.A$ (independent columns in A)
- All leading determinants > 0 (i.e. determinants of the leading principal minors) (demo here)
- All pivots in elimination > 0
Related material
- Positive Definite and Semidefinite Matrices (MIT OpenCourseWare)
No comments
 Donate
Donate