Definition: Laplacian Matrix for triangle meshes

Definition of the Laplacian matrix and Laplace operator on a triangular mesh. This is a cheat sheet / summary, I give an in depth explanation here.
Laplacian matrix (triangle mesh)
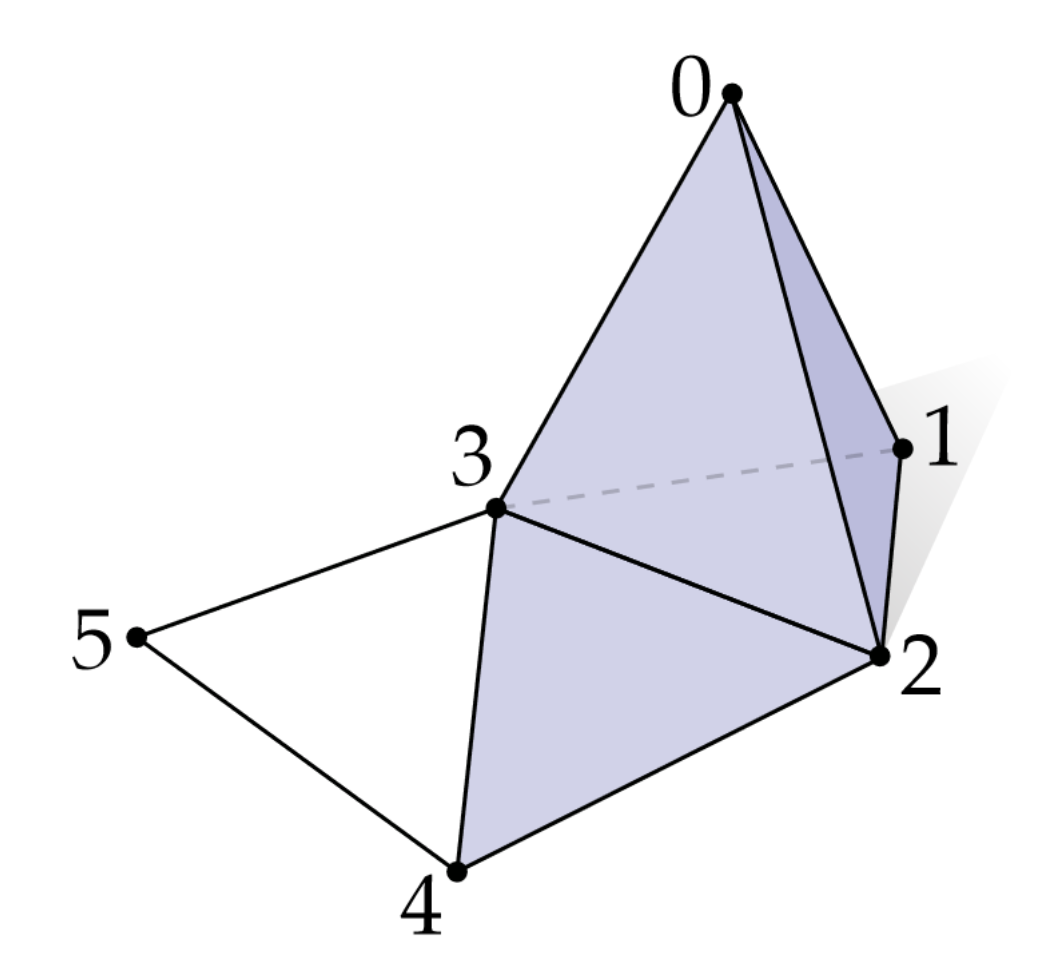
Visually the matrix is symmetric and reflects the adjacency graph of our mesh, see a concrete illustration below and notice how vertex \(0\) is connected to \(\{1, 2, 3\}\); vertex \(1\) to \(\{0, 2, 3\}\) and so on:
Formally, what is commonly called the Laplacian matrix \( \mathbf L \) in the literature of geometry processing is:
$$
\mathbf L_{ij} =
\left \{
\begin{matrix}
w_{ij} & = & \frac{1}{2} (\cot \alpha_{ij} + \cot \beta_{ij}) & \text{ if j adjacent to i} \\
& ~ & -\sum\limits_{{j \in \mathcal N(i)}} { w_{ij} } & \text{ when } j = i \\
& ~ & 0 &\text{ otherwise } \\
\end{matrix}
\right .
$$
- \( \mathbf L \in \mathbb R^{n \times n} \) with \( n \) the number of vertices of the mesh
- \( \mathbf L_{ij} \) is a single element of the matrix
- The row \( i \) and column \( j \) of the matrix represent vertex indices as well
- \( {j \in \mathcal N(i)} \) is the list of vertices directly adjacent to the vertex \( i \)
- Each row of \( \mathbf L \) contains the list of vertices weights adjacent to \( i \)
- \( \mathbf L \) is symmetric positive semi-definite
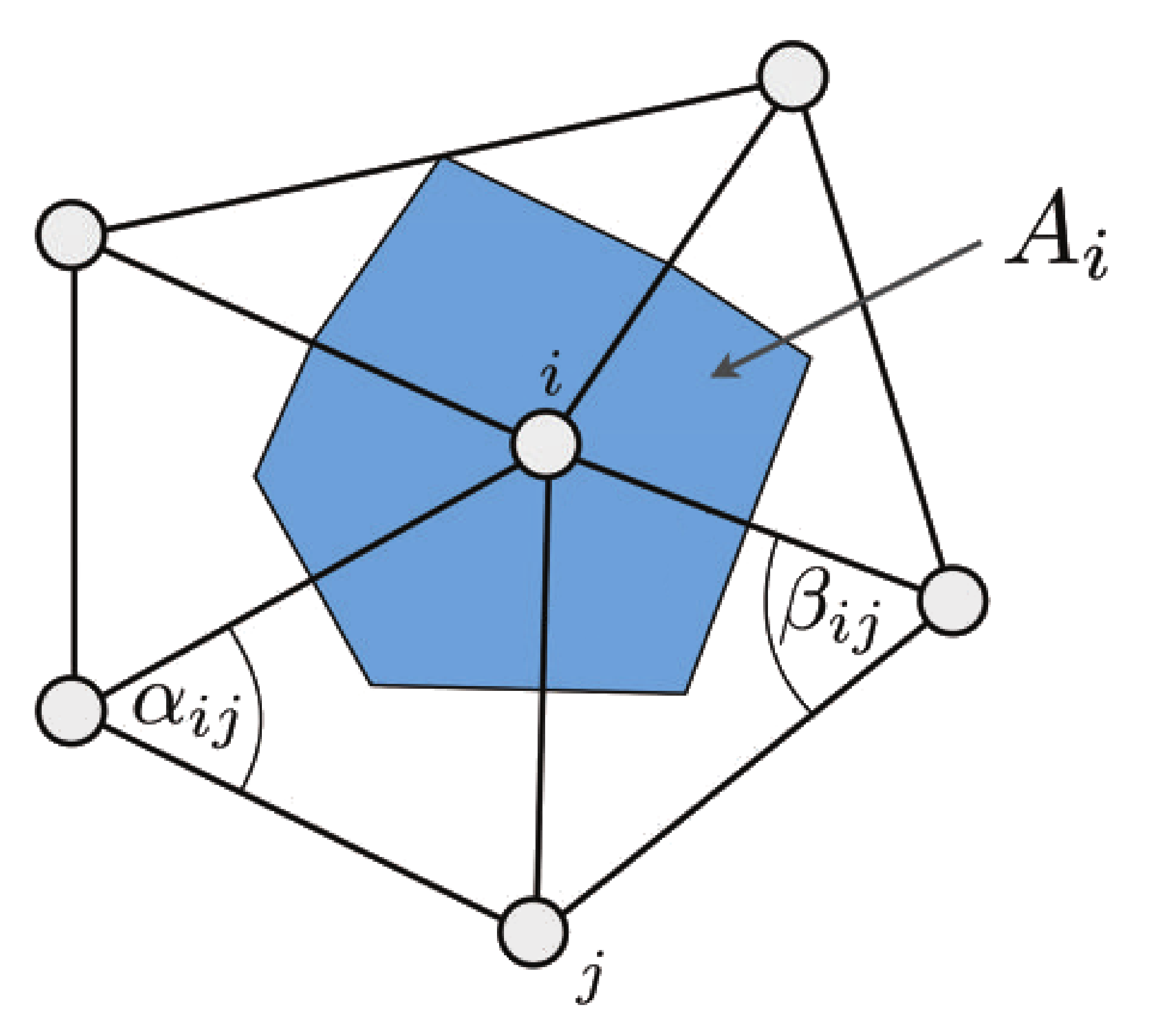
- \( \cot \alpha_{ij} \) and \( \cot \beta_{ij} \) is the evaluation of the cotangent function at \(x= \alpha_{ij} \) and \(y = \beta_{ij} \) (c.f. figure below)
\( \cot( \theta ) = \frac{\cos \theta}{\sin \theta} =\frac{\vec u . \vec v}{ \|\vec u \times \vec v\|} = \frac{\|\vec u\|.\|\vec v\| cos(\theta) }{\|\vec u\|.\|\vec v\| sin(\theta)} \)
Remark: the general Laplacian matrix as defined in graph theory (as opposed to geometry processing like in here) is usually defined as \( -\mathbf L \)
Discrete Laplace operator
On the other hand the Laplacian *operator* is defined as \( \mathbf {\Delta f} = {\mathbf M}^{-1} \mathbf L \) with the Mass matrix \( \mathbf M \), a diagonal matrix that stores the cell area (blue area on the figure) of each vertex:
$$
\mathbf M^{-1} =
\begin{bmatrix}
\frac{1}{A_0} & 0 & 0 \\
0 & \ddots & 0 \\
0 & 0 & \frac{1}{A_n}\\
\end{bmatrix}
$$
$$A_i = \frac{1}{3} \sum\limits_{{T_j \in \mathcal N(i)}} {area(T_j)}$$
- \( T_j \in \mathcal N(i) \) list of triangles adjacent to \( i \)
- \( A_i \) can also be computed with mixed voronoi area.
Code
See the [ ![]() C++ code ]
to build the laplacian matrix with cotan weights (
C++ code ]
to build the laplacian matrix with cotan weights (get_laplacian() procedure)
If your mesh is represented with an half-edge data structure (each vertex knows its direct neighbours) the pseudo code to compute \( \mathbf L \) is:
// angle(i,j,t) -> angle at the vertex opposite to the edge (i,j)
for(int i : vertices) {
for(int j : one_ring(i)) {
sum = 0;
for(int t : triangle_on_edge(i,j))
{
w = cot(angle(i,j,t));
L(i,j) = w;
sum += w;
}
L(i,i) = -sum;
}
}
On the other hand the Laplacian \( \mathbf L \) may be built by summing together contributions for each triangle, this way only the list of triangles is needed:
for(triangle t : triangles)
{
for(edge i,j : t)
{
w = cot(angle(i,j,t));
L(i,j) += w;
L(j,i) += w;
L(i,i) -= w;
L(j,j) -= w;
}
}
No comments
 Donate
Donate