Implicit surface a.k.a (signed) distance field: definition

If I say "implicit surface" you may think of metaballs and marching cube, I'll show you there is more to it!
\( \renewcommand{\vec}[1]{ \mathbf{#1} } \)Keywords
In this article we indifferently talk about (Signed) Distance Fields (SDF) or implicit surfaces. They both designated the same thing. In the game industry "distance fields" is the more commonly used term, while in the academic (scholar) world "implicit surface" is often preferred. There are other less common designation for distance fields such as:
- scalar field
- potential field
- density field
When referring to the combination of distance field we may talk about "implicit blending" or "implicit surface composition".
Introduction
When people hear "implicit surface" most of them think about metaballs, blobby objects and the marching cube. I want to define here implicit surface as a much more general concept and basic jargon related to this field. Let's be clear from the start, implicit surfaces are not just metaballs! Nowadays you can model virtually anything with implicit surfaces, from simple shapes like cubes, cylinders etc. to very intricate shapes such as human characters or creatures. Implicit surfaces can represent sharp edges and are not just limited to soft shapes. Some nice rendering of implicit surfaces also known as (signed) distance fields:




Considering only metaballs and the marching cube for implicit surfaces would be the equivalent of thinking only about clothes and rasterization when talking about meshes. With both you can model a variety of 3D models and both can be rendered in various ways (raytracing etc.). Another common bias is to think of implicit surfaces a.k.a (signed) distance fields only as mathematical equations. This is wrong, for instance voxel grids can be used to store implicit surfaces.

Other popular games based on or using implicit surfaces:
- Claybook (Real time raytracing of implicit surfaces with ambient occlusion and all)
- Dreams (Real time raytracing)
- Spore (In particular the character customization and the way you could freely add limbs)
What they are not
Before defining what is an implicit surface I always like to define it's counterpart first: explicit surfaces. An explicit surface can be triangular mesh, a parametric surface (e.g. splines, nurbs, ...) and so on, anything that explicitly represent a surface. For instance, take a look a the parametric function \( s : \mathbb R^2 \rightarrow \mathbb R^3\) this function takes in input 2 parameters \((u,v)\) and returns a point \((x,y,z)\) directly on the surface. We can explicitly and directly extract points on the surface.
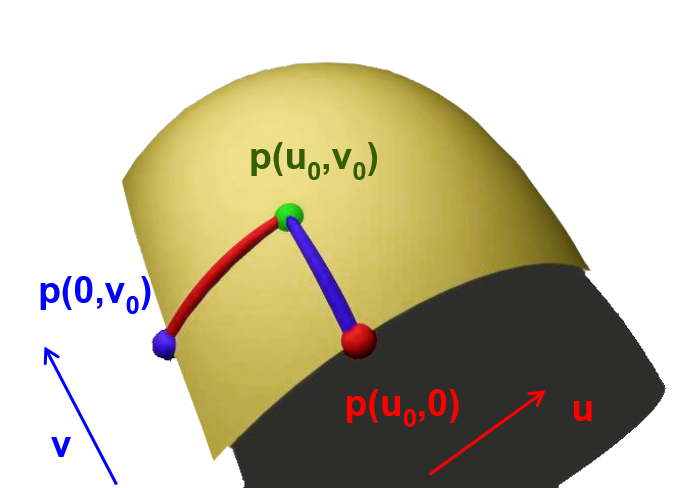
On the other hand the volume is implicit, even if the parametric surface or mesh represent a closed object, determining if a point in space \( \vec p \) is inside or outside the object will be more tricky.
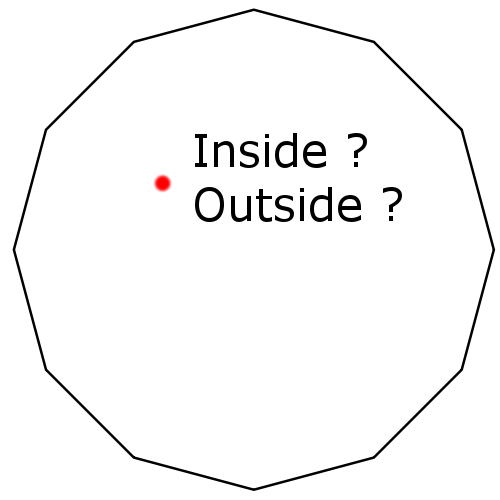
What they really are
It's not a surface it's a volume!
Implicit surfaces are actually explicit volumes they explicitly define what is the inside and outside of your object. Let's define it formally. Consider the function \( f:\mathbb R^3 \rightarrow \mathbb R \) this function takes a 3D point \( (x,y,z) \) in input and returns a single value. This value tells us explicitly if we are outside or inside the volume:
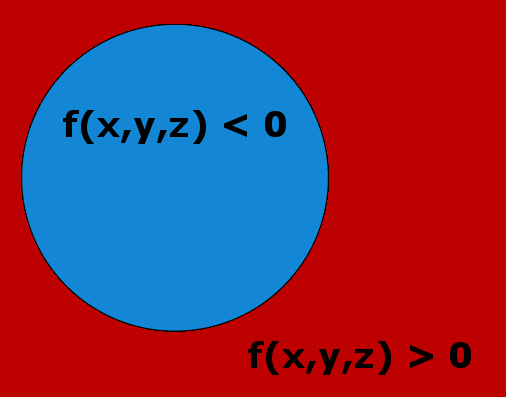
$$
\begin{array}{ll}
f(x,y,z) > 0 & \color{red} \text{ are points outside the object }\\
f(x,y,z) < 0 & \color{blue} \text{ are points inside the object }\\
\end{array}
$$
On the other hand, the surface is defined implicitly, there is no way to compute directly from \(f\) points on the surface or it will need some extra efforts. An implicit surface is then defined as follow:
$$ f(x,y,z) = 0 \color{grey} \text{ are points on the surface} $$

Let's define an implicit surface with the equation of a sphere whose center is \(\vec c \in \mathbb R^3\) and radius \( r \):
$$
\begin{array}{llll}
f( \vec p ) & = & \| \vec p - \vec c \| - r & \\
f(x,y,z) & = & \sqrt{(x-c_x)^2 + (y-c_y)^2 + (z-c_z)^2 } - r& \\
\end{array}
$$
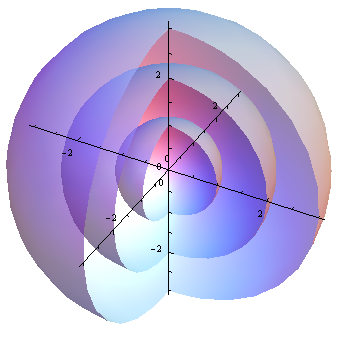
For points \( \vec p \) at a distance \( r \) from the center \(\vec c\) of the sphere \(f(\vec p) = 0\):

Iso-surface
What \(f(\vec p) = 0\) defines is the \( 0\text{-isosurface} \). We can actually define an infinity of implicit surfaces from the sphere's equation. Consider \( f(\vec p) = iso\) then for \(iso = -2.3\) you have the \( -2.3\text{-isosurface} \), for \(iso = 0.1\) the \( 0.1\text{-isosurface} \) and so on.
Scalar-field
The function \( f \), which now we know defines a volume, is also sometimes called scalar-field. It associates to every 3D points in space (the field) a single real value (a scalar). For instance imagine \( f \) indicates the temperature of a room at any point in space:
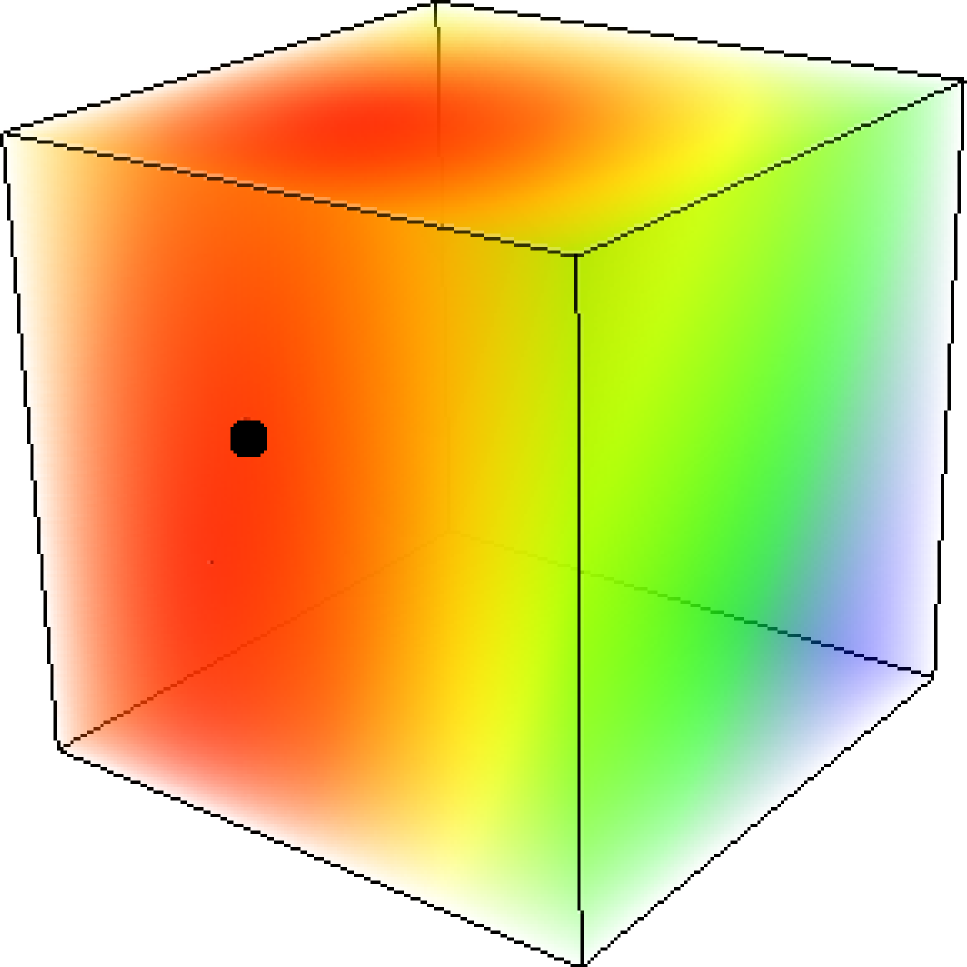
You could possibly extract the iso-surface for points at a 20C° temperature and see what area of the room is below 20C°. Sometimes instead of the word 'scalar' the term 'potential' is used, and \( f \) then describes a 'potential-field' but this is only a matter of taste.
Distance field
Yet another way to look at this function \(f : \mathbb R^3 \rightarrow \mathbb R\) is to interpret it as a distance field. For instance \( f( \vec p) = \| \vec p - \vec c \| - r \) actually returns the signed distance from the point \( \vec p \) to the surface of the sphere of radius \( r \).

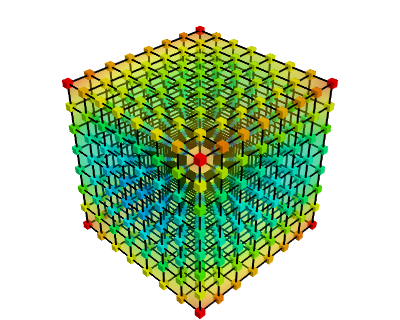
Voxels
You can use a 3D grids (3D textures, voxels etc.) to store values of \( f \) (a sample). When sampling the function \( f \) on a regularly spaced grid: \( f(0,0,0) \), \( f(0.1,0,0) \), \( f(0.2,0,0) \) etc. you can then get the intermediate values (e.g. \(f(0.15,0,0)\)) with tri-linear interpolation.
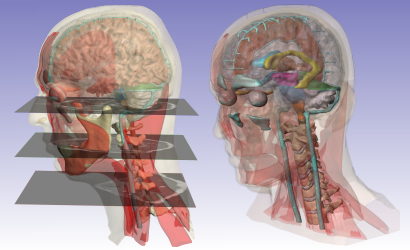
A more concrete example are MRI where you get a stack of textures describing the density of the body and from which you could extract the surface of the organs.
Wrapping up
An implicit surface is defined by the equation \(f(\vec p) = iso\) with \(f\) actually defining a volume and is known under many names: scalar / potential / (signed) distance / density field. \(f\) can be defined with mathematical equations (sphere, cylinder, ellipse...) but the same way we have triangle meshes to represent a surface we can store the volume of \( f \) into a 3D grid. One popular method is to pre-calculate distance fields with the GPU using shaders before storing it into a 3D texture.
In future posts we'll see that contrary to explicit surface representations such as meshes, implicit surfaces are extremely easy and robust when it comes to combine and blend them together. This is usually called Constructive Solid Geometry or boolean modeling:
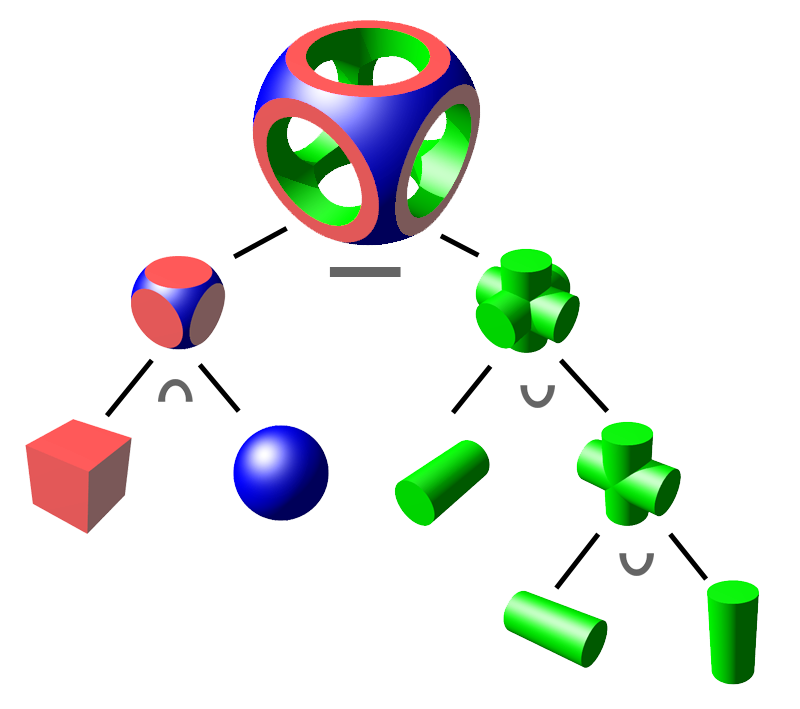
Lastly it is extremely useful for collision detection since you only have to check the sign of \(f\) to determine if you are inside or outside the considered object. For instance, physic simulation in games may convert objects to signed distance fields in order to efficiently solve collisions.
The main difficulty resides into rendering implicit surfaces, and can be computationally costly. Mainly two methods exists, conversion to a triangle mesh with the marching cube algorithm or ray marching.
No comments
 Donate
Donate