Cyclic Coordinate Descent Inverse Kynematic (CCD IK)

The goal of Inverse kinematic is simple, given a target point in space \( T \) (blue cube) find the best rotation for each joint so that the tip of the last joint reaches the target. Many algorithms exist and the one presented below is called CCD IK. You can also constraint joints to rotate around specific axis (option box: CCD+hinge) or to only rotate within a certain range (option box: CCD+hinge+range), you can test it out with the javascript/webgl snippet below:
Inspired by the blog post of Johnathon Selstad on CCD IK as an exercise for myself I wanted to re-word the post and implement my own shader toy version as well as the above custom javascript version.
Summary of the simple CCD Inverse Kynematic algorithm
- \( T \) : Position of the target
- \( E \) : Position of the end-effector (tip of the last joint)
- \( O \) : Pivot point of the ith link, \( i=1, 2, …, n \)
- \( t_i \): Target vector for the ith link = \( T - O_i \)
- \( e_i \) : End-effector vector for the ith link = \( E − O_i \)
- \( \alpha_i\) : Angle between vectors \( t_i \) and \( e_i \) .

The core of the CCD IK algorithm is extremely simple:
for( r = 0; r < nb_iterations; r++){
// Iterate from tip to base
for( i = n; i > 0; --i){
rotation_i = rotation_between(e_i, t_i)
// rotate ith link by alpha_i so that the end-effector meets the target vector ti
joint[i].rotate_by( rotation_i )
}
}
Constraining the rotation to a specific axis is quite simple as well. Let \( axis_i \) be the current axis, given the ith CCD rotation found in the first step we rotate \( axis_i \) which gives us the new axis \( axis_i' \). We just rotate back the ith joint by the rotation defined between \( axis_i \) and \( axis_i' \):
for( r = 0; r < nb_iterations; r++){
for( i = n; i > 0; --i){
rotation_i = rotation_between(e_i, t_i)
joint[i].rotate_by( rotation_i )
current_axis = rotation_i * joint[i].axis;
rotation_back = rotation_between( current_axis, joint[i].axis )
joint[i].rotate_by( rotation_back )
}
}
Now we can constrain the range of the rotation as well. Wether your rotations are represented by a Quaternion or a Matrix you can extract the pair (axis, angle), clamp the angle and convert back to the final matrix/quaternion:
for( r = 0; r < nb_iterations; r++){
for( i = n; i > 0; --i){
rotation_i = rotation_between(e_i, t_i)
joint[i].rotate_by( rotation_i )
current_axis = rotation_i * joint[i].axis;
rotation_back = rotation_between( current_axis, joint[i].axis )
joint[i].rotate_by( rotation_back )
(axis, angle) = extract_axis_angle( joint[i].get_rotation() )
joint[i].set_rotation( build_rotation(axis, clamp(angle, min, max)) )
}
}
Reference
Bonus: FABRIK
Found some code for the FABRIK algorithm see it live here
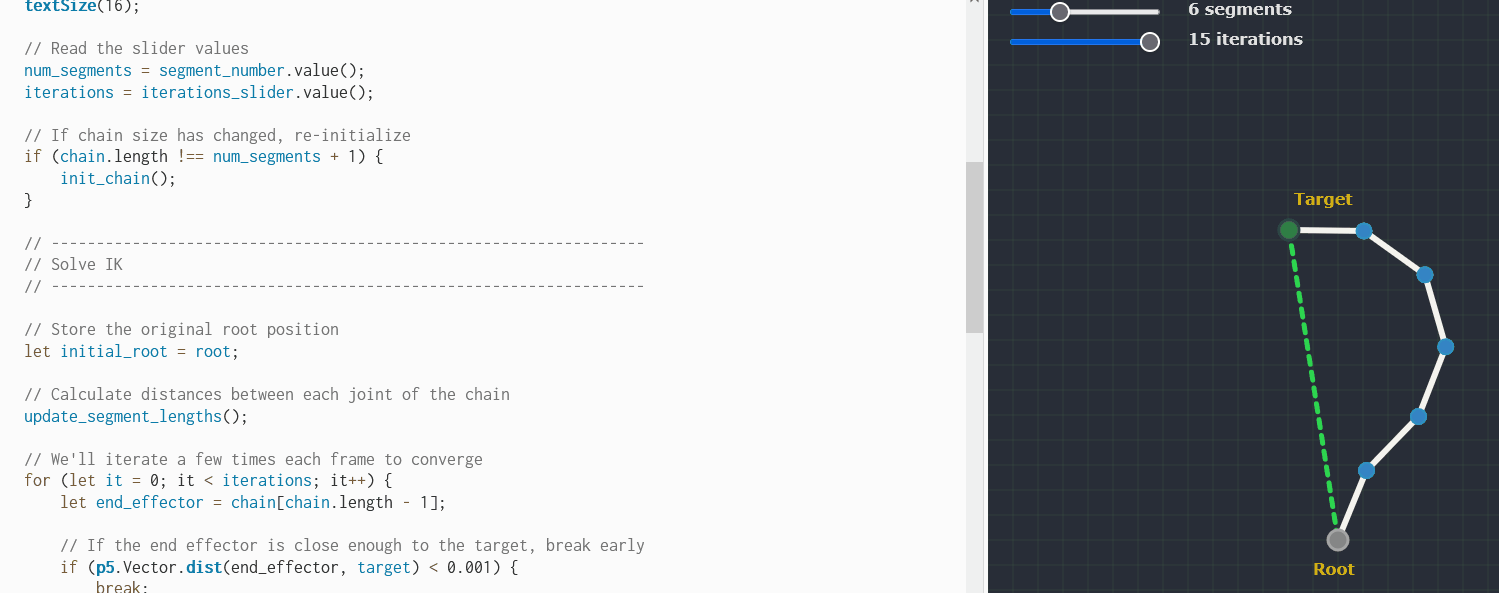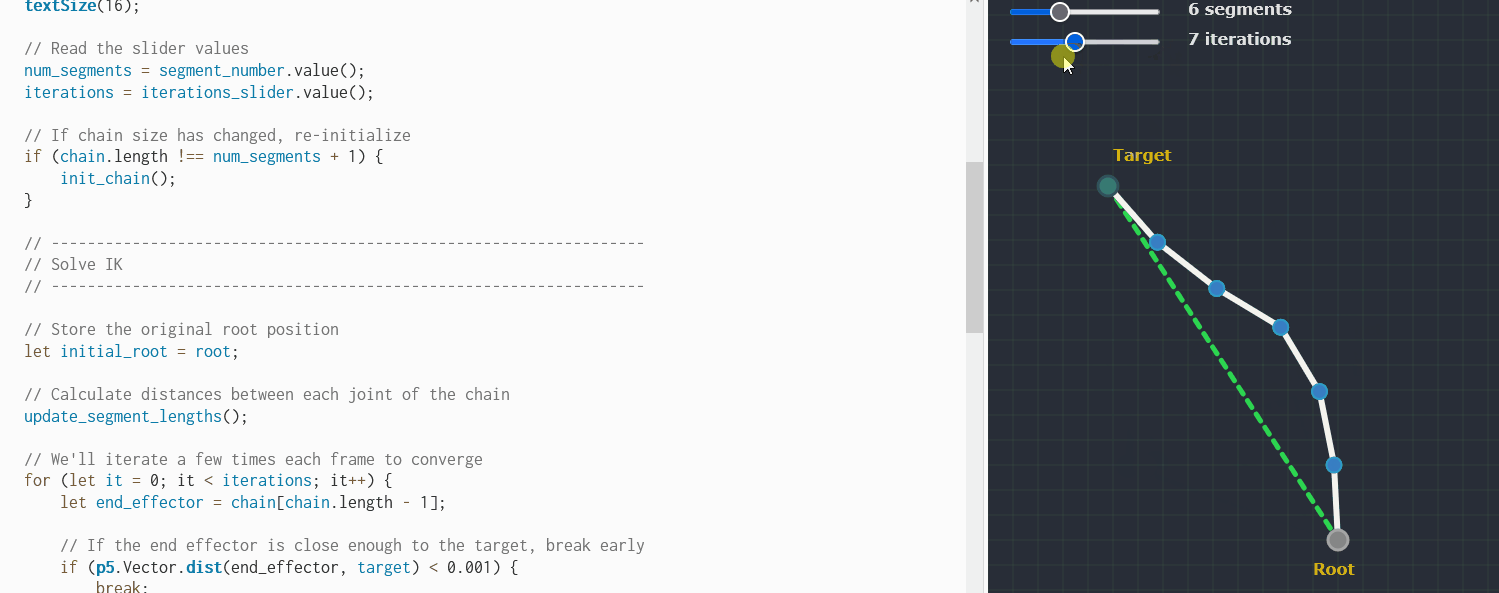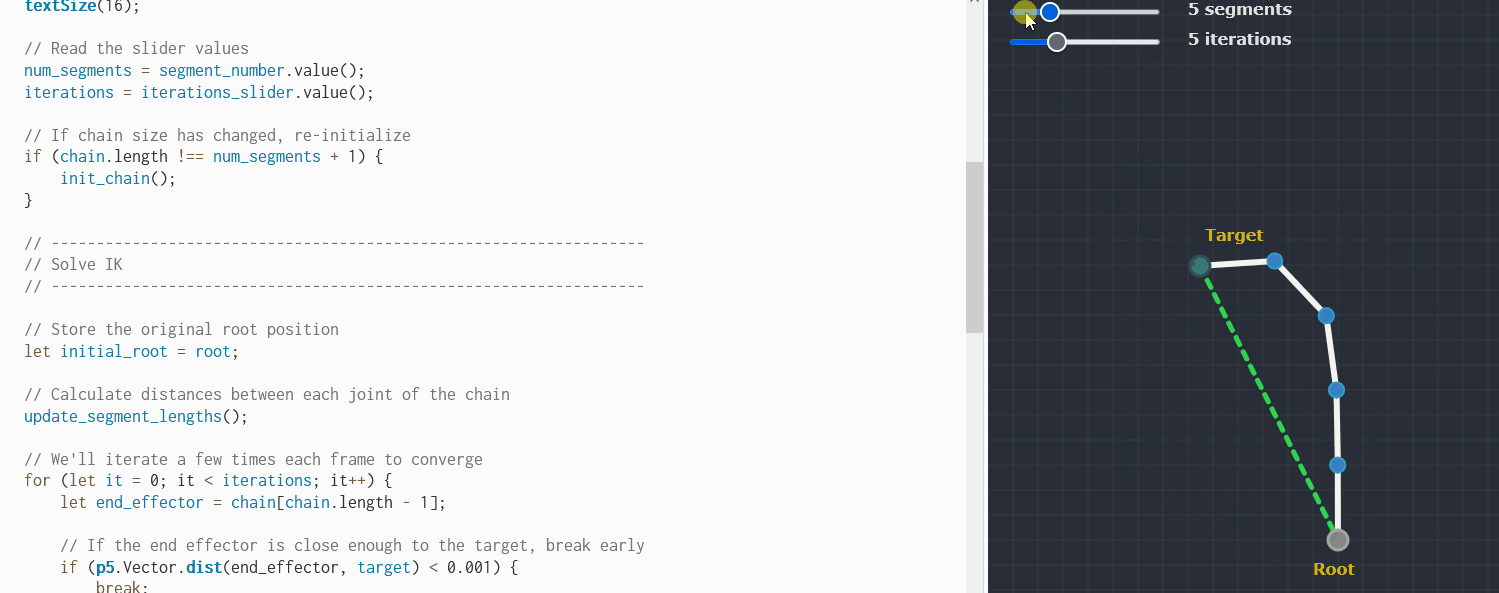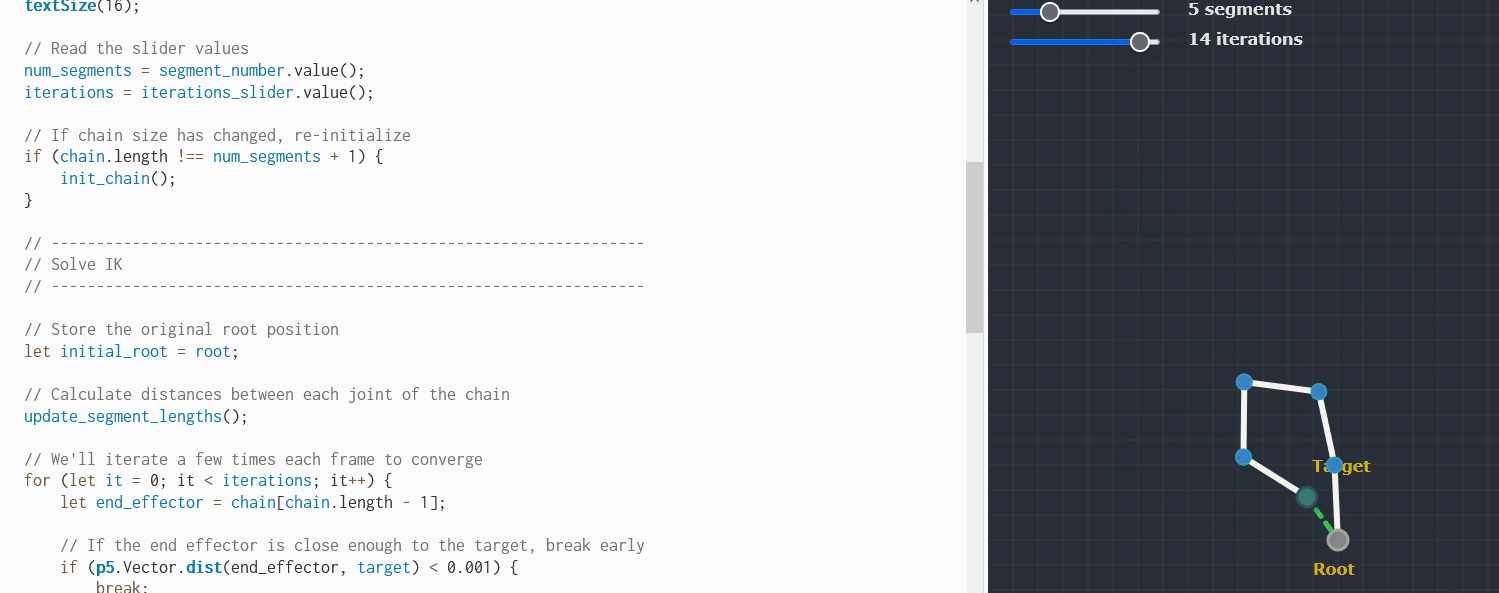
let chain = [];
let segment_length = 75;
let num_segments = 2;
let iterations = 1;
let draggingTarget = false;
let draggingRoot = false;
let target; // Position of the "target"
let root; // Position of the root
let segment_lengths = []; // Array to store the length of each segment
function setup() {
createCanvas(700, 700);
// slider to pick the number of segments
segment_number = createSlider(2, 15, 2, 1);
segment_number.position(20, 10);
segment_number.style('width', '150px');
// slider to set iterations
iterations_slider = createSlider(1, 15, 15, 1);
iterations_slider.position(20, 40);
iterations_slider.style('width', '150px');
// Initialize the position of the target
target = createVector(400, 250);
root = createVector(width / 2, height - 150);
// Initialize the chain
init_chain();
}
function draw() {
background(40, 45, 55);
drawGrid();
stroke(0);
fill('white');
textSize(16);
// Read the slider values
num_segments = segment_number.value();
iterations = iterations_slider.value();
// If chain size has changed, re-initialize
if (chain.length !== num_segments + 1) {
init_chain();
}
// ------------------------------------------------------------------
// Solve IK
// ------------------------------------------------------------------
// Store the original root position
let initial_root = root;
// Calculate distances between each joint of the chain
update_segment_lengths();
// We'll iterate a few times each frame to converge
for (let it = 0; it < iterations; it++) {
let end_effector = chain[chain.length - 1];
// If the end effector is close enough to the target, break early
if (p5.Vector.dist(end_effector, target) < 0.001) {
break;
}
// FORWARD REACHING
// Start from the target and work backwards to the root
// Set the end effector to the target position
chain[chain.length - 1] = target;
// Forward reaching: work from the end to the base
for (let i = chain.length - 2; i >= 0; i--) {
// Get the direction from the current joint to the next joint
let direction = p5.Vector.sub(chain[i + 1], chain[i]);
direction.normalize();
// Scale the vector back to segment length
let scaled_vec = p5.Vector.mult(direction, -segment_lengths[i]);
// Set new position of the current joint
chain[i] = p5.Vector.add(chain[i + 1], scaled_vec);
}
// BACKWARD REACHING
// Start from the root (constrained to original position) and work forwards
// Reset the root to its initial position
chain[0] = initial_root;
// Backward reaching: work from the base to the end
for (let i = 0; i < chain.length - 1; i++) {
// Get the direction from the current joint to the next joint
let direction = p5.Vector.sub(chain[i + 1], chain[i]);
direction.normalize();
// Scale the vector back to segment length
let scaled_vec = p5.Vector.mult(direction, segment_lengths[i]);
// Set new position of the next joint
chain[i + 1] = p5.Vector.add(chain[i], scaled_vec);
}
}
// ------------------------------------------------------------------
// Draw visualizers
// ------------------------------------------------------------------
strokeWeight(6);
stroke(244, 243, 238);
drawingContext.setLineDash([]);
fill(215, 180, 15);
noStroke();
text('Root', root.x - 25, root.y + 35);
text('Target', target.x + 5, target.y -25);
push();
strokeWeight(5);
stroke(45, 214, 80);
drawingContext.setLineDash([8]);
last_joint = chain[chain.length - 1];
line(last_joint.x, last_joint.y, chain[0].x, chain[0].y);
pop();
push();
strokeWeight(2);
stroke(212, 58, 58);
line(chain[chain.length - 1].x, chain[chain.length - 1].y, target.x, target.y);
pop();
for (let i = 0; i < chain.length - 1; i++) {
push();
strokeWeight(6);
stroke(244, 243, 238);
line(chain[i].x, chain[i].y, chain[i + 1].x, chain[i + 1].y);
pop();
push();
strokeWeight(2);
stroke(45, 155, 200);
fill(56, 126, 195,255);
ellipse(chain[i].x, chain[i].y, 15, 15);
ellipse(chain[i+1].x, chain[i+1].y, 15, 15);
pop();
}
noStroke();
fill(225);
text(`${num_segments} segments`, 200, 25);
text(`${iterations} iterations`, 200, 55);
push();
strokeWeight(3);
stroke(45, 80, 91);
fill(56, 123, 114);
ellipse(target.x, target.y, 20, 20);
pop();
push();
strokeWeight(3);
stroke(165, 165, 165);
fill(133, 133, 133);
ellipse(root.x, root.y, 20, 20);
pop();
fill(125, 125, 125, 135);
noStroke();
textSize(35);
textFont('Verdana');
textStyle(BOLD);
text('FABRIK', width * 0.74, height * 0.97);
textSize(20);
text('Forward and Backward Reaching Inverse Kinematics', width * 0.1, height * 0.92);
}
// --------------------------------------------------------------------
// Initialize the chain
// --------------------------------------------------------------------
function init_chain() {
chain = [];
segment_lengths = [];
// Base/root joint near bottom center
chain.push(root);
// Build segments upwards
for (let i = 0; i < num_segments; i++) {
let prev = chain[chain.length - 1];
chain.push(createVector(prev.x, prev.y - segment_length));
}
// Initialize segment lengths
update_segment_lengths();
}
// --------------------------------------------------------------------
// Update the lengths of each segment
// --------------------------------------------------------------------
function update_segment_lengths() {
segment_lengths = [];
for (let i = 0; i < chain.length - 1; i++) {
segment_lengths.push(p5.Vector.dist(chain[i], chain[i + 1]));
}
}
function mousePressed() {
// Check if the mouse is over the target
let distanceToTarget = dist(mouseX, mouseY, target.x, target.y);
if (distanceToTarget < 10) {
draggingTarget = true;
cursor('grab');
}
// Check if the mouse is over the root
let distanceToRoot = dist(mouseX, mouseY, root.x, root.y);
if (distanceToRoot < 10) {
// draggingRoot = true;
cursor('grab');
}
}
function mouseDragged() {
if (draggingTarget) {
target.set(mouseX, mouseY);
cursor('grab');
}
if (draggingRoot) {
root.set(mouseX, mouseY);
cursor('grab');
}
}
function mouseReleased() {
draggingTarget = false;
draggingRoot = false;
cursor('default');
}
function drawGrid() {
fill(0);
stroke(80, 125, 80, 50);
strokeWeight(1);
drawingContext.setLineDash([]);
for (let x = -width; x < width; x += 25) {
line(x, -height, x, height);
}
for (let y = -height; y < height; y += 25) {
line(-width, y, width, y);
}
}
No comments
 Donate
Donate