Summary: Permutation Arrangement Combination
There are 3 ways to make a disposition of objects:
Mnemonic: 3d PaC
Permutation arrangement Combination
- Ordered => "Permutation"
- Every object: any possible ordered disposition of \(n\) objects.
- With repetition \(n^n\)
- No repetition \(n!\)
- Subset of objects: "Arrangement" a disposition of \(k\) objects from a set of \(n\) objects.
- Unordered => "Combination"
Bag of stuff: pick \(k\) elements from \(n\) bins/objects. - With repetitions \(\binom{n+k-1}{k}\)
- No repetitions \(C^n_k =\binom{n}{k} = \frac{n!}{k!(n-k)!}\)
In permutation we just switch object positions until every combination is exhausted:
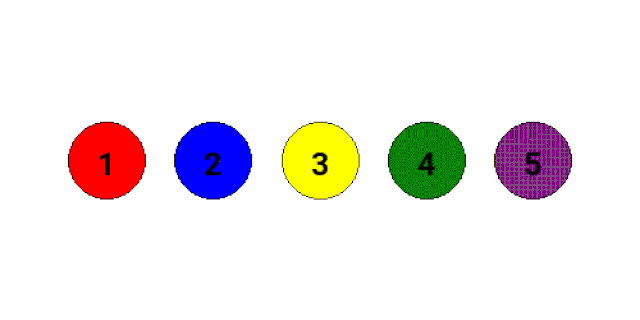
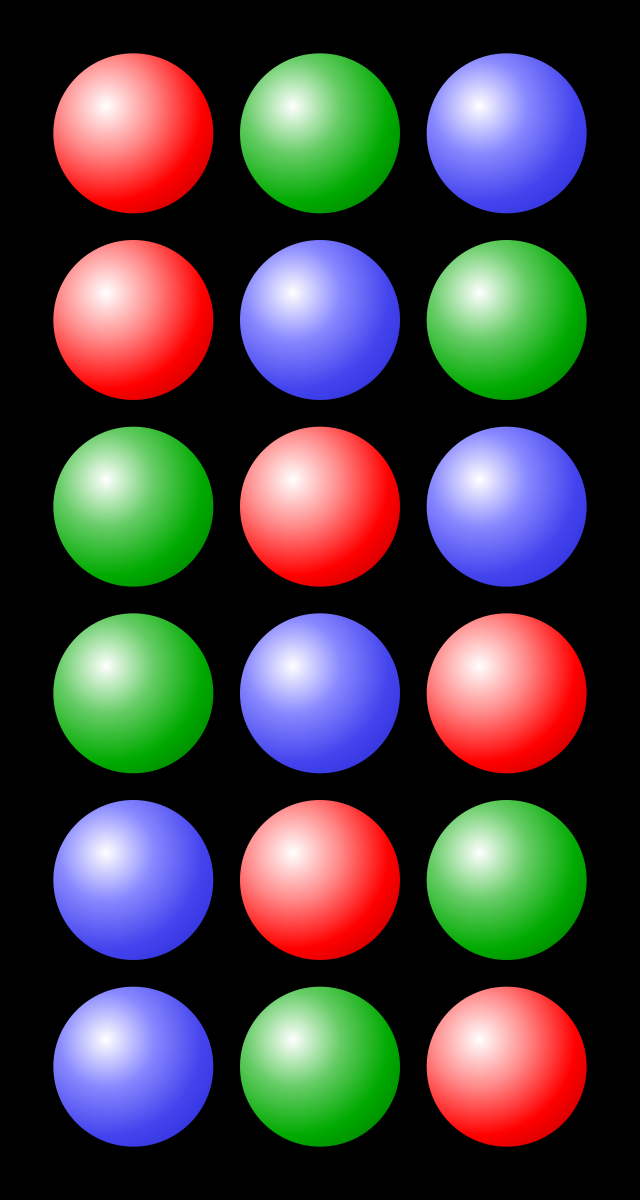

example:
3! = 6 123 321 213 231 132 312
Or with colors:

$ {4 \choose 3 } $ From a box of 4:

We pick 3 (order does not matter):
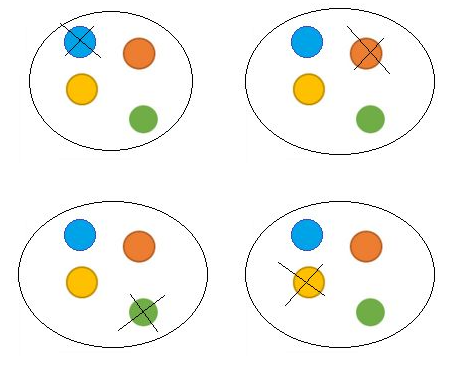
Note: Arrangement are often viewed as a sub-set of Permutations.
Other kind of dispositions:
No comments
 Donate
Donate