Mean curvature of a 2D function graph z = f(x, y)
You may want to look at the article where I define Principal/Gaussian/Mean curvature (the article focus on triangle mesh surface but the general definition applies for all kind of surfaces).
Formula
The Mean curvature of a surface described by a function $z = f(x, y)$ can be calculated using the formula:
$$ H = \frac{ f_{xx}(1 + (f_y)^2) - 2 f_{xy} f_x f_y + f_{yy}(1+ (f_x)^2) }{ 2(1+ (f_x)^2 + (f_y)^2)^{3/2}} $$$ \begin{align*} & f: \mathbb R^2 \rightarrow \mathbb R\\ & f_{xx} \text{ is the second partial derivative of } f \text{ with respect to } x \text{ twice} \\ & f_{yy} \text{ is the second partial derivative of } f \text{ with respect to } y \text{ twice} \\ & f_{xy} \text{ is the mixed partial derivative of } f \text{ with respect to } x \text{ and } y \\ & f_x \text{ is the partial derivative of } f \text{ with respect to } x \\ & f_y \text{ is the partial derivative of } f \text{ with respect to } y \text{ and} \\ & H \text{ is the Mean curvature} \\ \end{align*} $
Later we use $Hess(f)$ for the Hessian matrix of $f$ and disambiguate it from the mean curvature $H$.
Alternate formulation
From "Consistent Computation of First- and Second-Order Differential Quantities for Surface Meshes"
$$ H = \frac{ Trace(Hess(f))} { 2{\ell} } - \frac{\nabla f^T.Hess(f).\nabla f }{ 2 \ell^3} $$ Where: $$ \begin{aligned} &\ell &=& \quad \| \vec s_u \times \vec s_v \| \\ &\ell &=& \quad \sqrt{(1 + f_x^2 + f_y^2)} \\ &\ell^2 &=& \quad (1 + f_x^2 + f_y^2) \\ &\ell^4 &=& \quad (1 + f_x^2 + f_y^2)^2 \\ \end{aligned} $$And $\vec s$ is a parametric function defined as below with $\vec s_u$ and $\vec s_v$ are respectively the partial derivatives in $u$ and $v$:
$$ \vec s(u,v) = \left \{ \begin{aligned} x(u,v) &= u \\ y(u,v) &= v \\ z(u,v) &= f(u,v) \end{aligned} \right . $$Remarks
The following observations are particularly useful in the context of solving optimization problems and finding the minimal value of a function.
For the specific case of a point $p(x,y)$ where the gradient is null $\nabla f = 0$ (i.e. $f_x=0$ and $f_y=0$) then the Mean curvature of $f$ is half of the trace of the hessian $Tr(Hess(f))/2$. Usually, we are only interested by the sign of the Mean curvature $H$; so it is not unusual to see $H$ simplified as $H = Tr(Hess(f))$. Since the trace is the sum of the Eigen values, at $\nabla f = 0$, we can also say that $H$ is the sum of the Eigen values $\lambda_1$ and $\lambda_2$ of the Hessian matrix.
Note that by definition, the Hessian matrix is positive definite when its Eigen values are all positives. So a positive definite Hessian at a point $p$ where $\nabla f(p) = 0$ necessarily means the function is bowled shaped (since the Gaussian curvature $K$ is positive as well) and convex. This property is used to find the minimum of a function in optimization problems. For a negative definite Hessian both Eigen values will be negative which indicates the Gaussian curvature $K$ is positive as well but the mean curvature $H$ negative, therefore the surface will be concave. (see Gaussian curvature of a 2D function z = f(x, y))
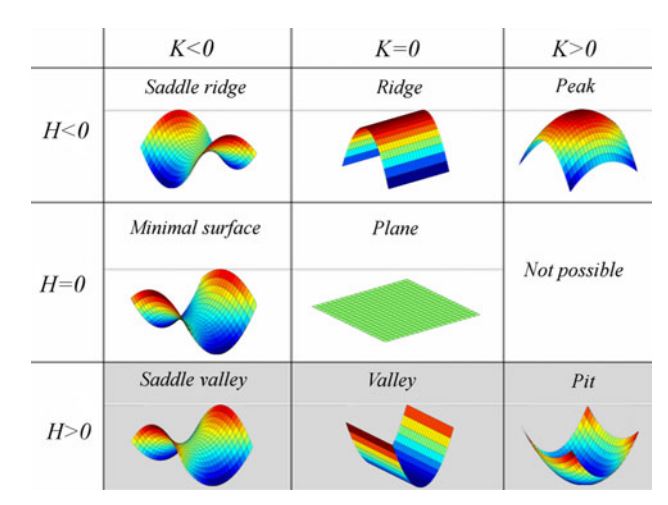
Note on principal curvatures: since $H = (\lambda_1 + \lambda_2)/2$ at $\nabla f(p) = 0$ by the very definition of the Mean curvature ($H = (\kappa_1 + \kappa_2)/2$) we can see that each Eigen value represents the principal curvatures ($\kappa_1 = \lambda_1$ and $\kappa_2 = \lambda_2$
Derivation
Treat $f(x,y)$ as a parametric function { x(u,v) = u; y(u,v) = v; z(u,v) = f(u,v)}. plug this vector valued function into the general formula $ H = \frac{L \ G - 2 \ M \ F + N \ E}{2 ( E \ G - F^2)}$ to compute the mean curvature of a parametric surface and develop. (see this course notes for more details)
No comments
 Donate
Donate