Maya math node summary

Maya math nodes
A small list of useful Maya nodes, I only list some of the most useful math nodes here. You may look up the official doc first:
Some nodes are not documented, you will have to go to the node editor press 'tab' and search for yourself... some of those undocumented nodes are listed here.
Expressions
If you don't find the native Maya node you are looking for, Maya animation expressions might do the job. Expression nodes are notoriously slow but allows for quick prototyping, also keep in mind that it is named based and any object renaming will potentially break your expressions.
A list of available functions inside an expression:
- math functions: trunc(), ceil(), floor() clamp(min, max, value), sin(), cos(), tan(), min(), max(), sqrt(), exp(), log(), sign() (and other trig functions ...)
- Random functions: gauss(), noise(), dnoise(), rand(), sphrand(), seed()
- Vector functions: angle(), cross(), dot(), mag(), rot(), unit()
- Conversion functions: deg_to_rad(), rad_to_deg(), hsv_to_rgb(), rgb_to_hsb()
- Array functions: clear(), size(), sort()
- Curve functions: linstep(), smoothstep(), hermite()(vector), hermite()(scalar)
Bifrost
Bifrost is a powerful node system usually known for its ability to simulate fluids, smokes and such,
but that can be used to work on geometry as well, and provides all the basic and more advanced math nodes and help you with rigging.
(See also Autodesk Japan bifrost tutorials on skin collision)
Native nodes
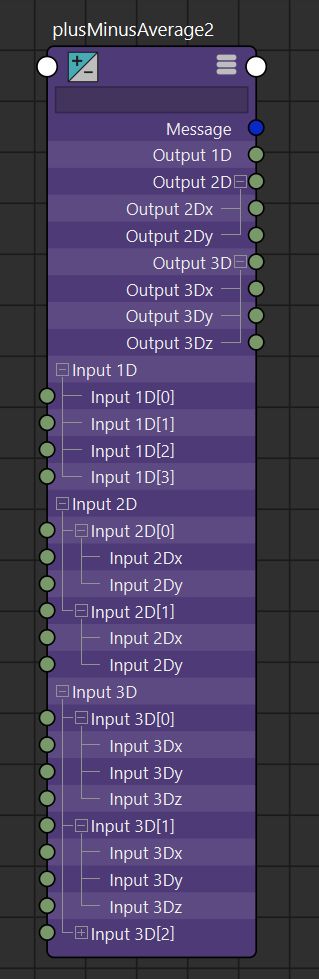
plusMinusAverage math node specification. Originally designed with shaders in mind those operations work on vectors, i.e. addition, division etc is usually applied on a per component basis (out.x = in1.x + in2.x), (out.y = in1.y + in2.y) etc. only supports floats
Related see: "addDoubleLinear", "substract" or "average" nodes for double attributes (works only on scalars though).
|
Note: when disconnecting make sure to reset the value of the attribute, otherwise it will keep adding, subtracting etc. whatever was the value at disconnection. |
  |
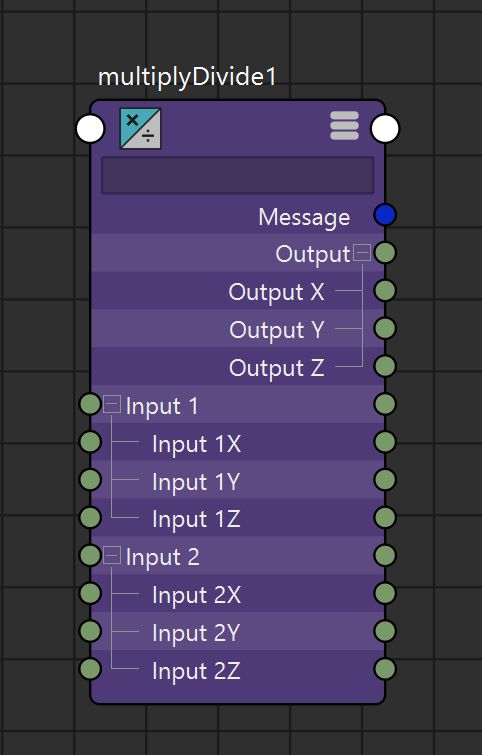
multiplyDivide math node specification. (for float attributes)
(to work with doubles see "divide" node or multDoubleLinear) (only scalars though)|
NO OPERATION: |
  |
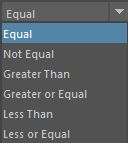
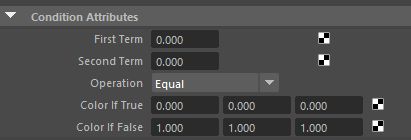
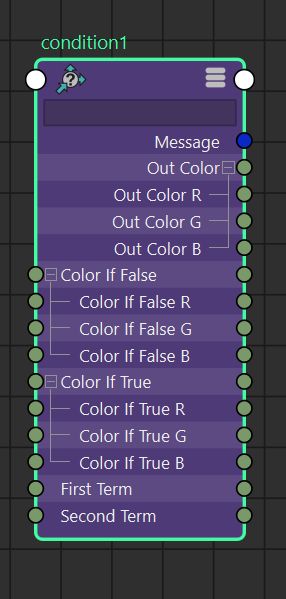
condition math node specification. Compare 'firstTerm' and 'secondTerm' with some boolean operator (<,>,== etc.) OutColor is assigned ColorIfTrue or ColorIfFalse according to the result of the operation.
if( firstTerm operation secondTerm ){
OutColor.r = ColorIfTrue.r
OutColor.g = ColorIfTrue.g
OutColor.b = ColorIfTrue.b
} else {
OutColor.r = ColorIfFalse.r
OutColor.g = ColorIfFalse.g
OutColor.b = ColorIfFalse.b
}
|
   |
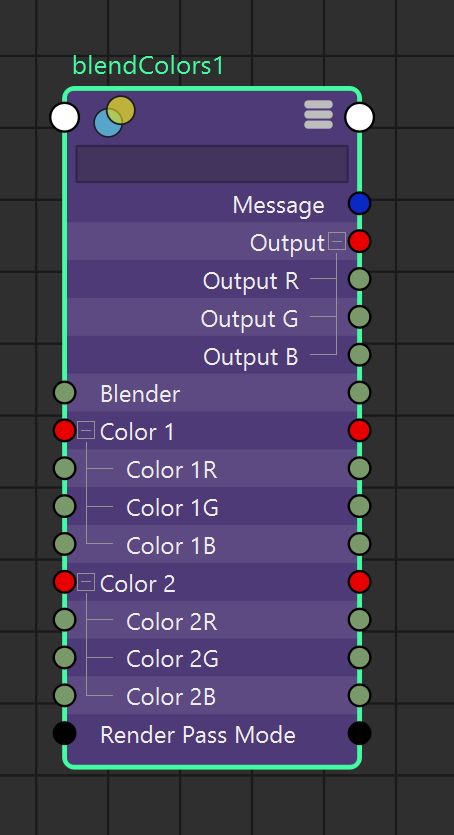
BlendColors math node specification. Linear interpolation between Color1 and Color2 given the parameter \( blender \in [0.0, 1.0]\).
Note: starting Maya 2024 we have the lerp(input1, input2, weight) node, that works with doubles.
| Output = Color1.rgb * (1.0 - blender) + Color2.rgb * blender |
 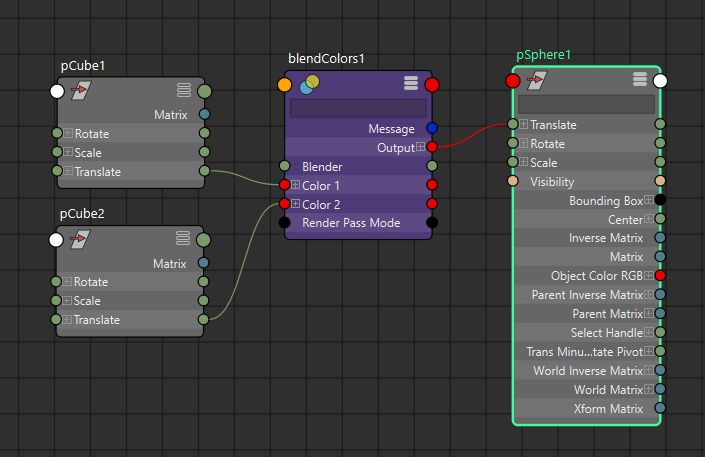 |
lerp math node specification. Linear interpolation between double input1 and double input2 given the parameter \( weight \in [0.0, 1.0]\).
Note: available from Maya 2024.
| Output = Input1 * (1.0 - weight) + Input2 * weight |
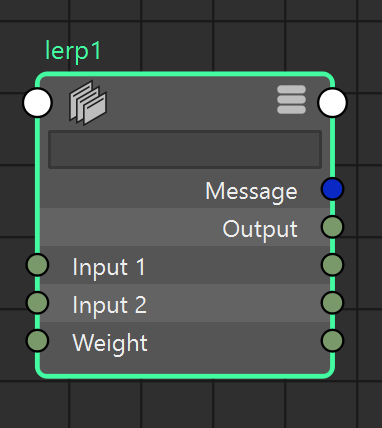 |
Reverse math node specification. Reverse a parametric parameter: Output = 1.0 - Input.
|
Output.x = 1.0 - Input.x Output.y = 1.0 - Input.y Output.z = 1.0 - Input.z |
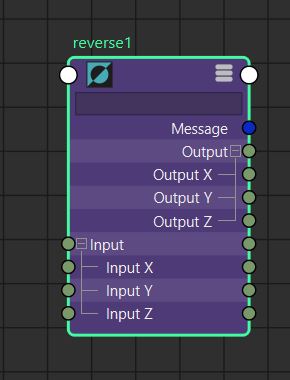 |
Note: 'animCurve' node is similar but always prefer 'remapValue' which is really fast to evaluate contrary to the 'animCurve' node.
OutputValue = Curve( InputValue ) Where the function "float Curve(float)" is the curve displayed in the attribute editor and which control points are stored in the "Value[]" attribute; OutputColor.RGB = Gradient( InputValue ) Where the function "Vec3 Gradient(float)" is the gradient strip displayed in the attribute editor and which interpolated colors are stored in the "Color[]" attribute |
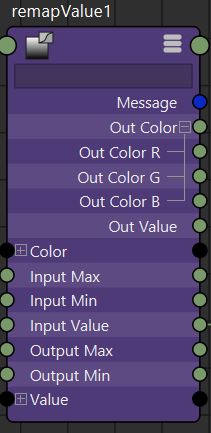 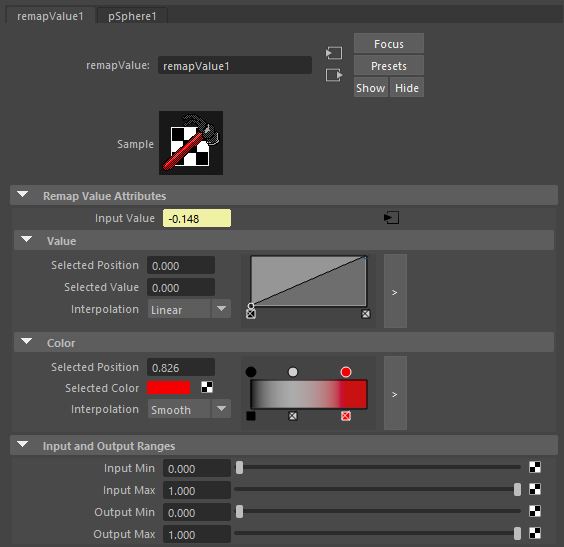 |
Not covered here:
- pointMatrixMult (matrix multiplication against vector or point) (double)
- See also (starting Maya 2024) (also double):
multiplyPointByMatrix, multiplyVectorByMatrix
- vectorProduct (dot product, cross product, vector or point matrix product) (floats)
- For doubles (starting Maya 2024):
crossProduct, dotProduct, vectorMatrix, pointMatrix
- clamp (clamp(vec3, minVec3, maxVec3))
- "min", "max" (out = minimum or maximum of a list of doubles) (undocumented)
- multDoubleLinear (scalar multiplication: out = realValue1 * realValue2) (double)
- addDoubleLinear (scalar addition: out = realValue1 + realValue2) (double)
- pointConstraint
can be used to compute the barycenter of several points (outPoint3 = ∑ point_i / n)
Trigonometry
Before Maya 2024 trigonometric functions (sin, cos etc) were not natively supported.
You could emulate trigonometry functions using some built-in nodes.
Matrices
Official list of built in matrix nodes
Multiplication order, from right to left as we increase the index:
Indices: n ... 1 0 Matrix : mat_n * ... * mat_1 * mat_0
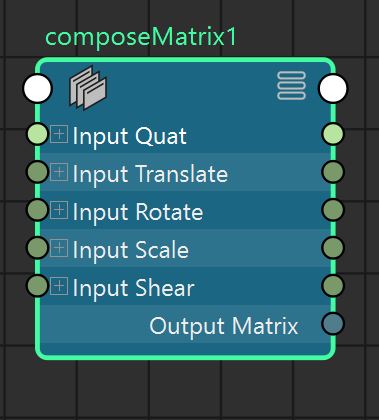
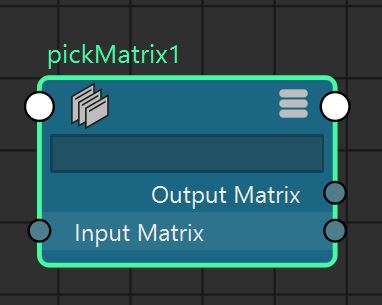
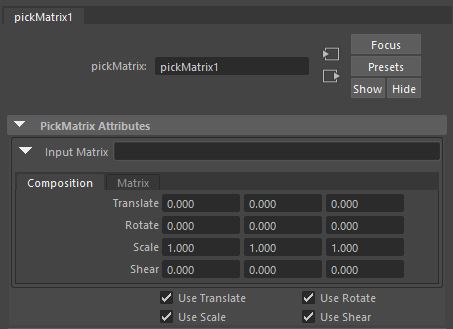
Other nodes not covered here (see matrix utility doc): addMatrix, aimMatrix, blendMatrix, composeMatrix, fourByFourMatrix, holdMatrix, passMatrix, pickMatrix, uvPin, proximityPin
\( MatrixSum = \prod_{i=n}^{0} MatrixIn[i] \)
MatrixSum = MatrixIn[n] * ... * MatrixIn[1] * MatrixIn[0] |
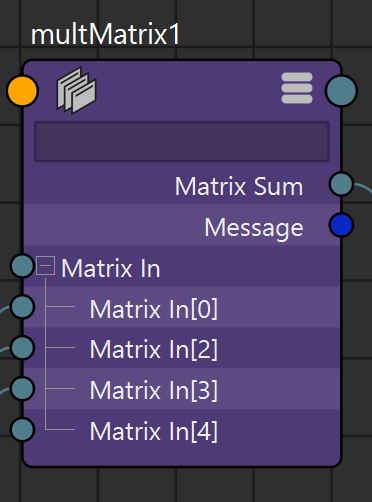 |
\( MatrixSum = \sum_{i=n}^{0} WtMatrix[i].MatrixIn * WtMatrix[i].WeightIn \)
MatrixSum =
WtMatrix[n].MatrixIn * WtMatrix[n].WeightIn *
... *
WtMatrix[0].MatrixIn * WtMatrix[0].WeightIn *
WtMatrix[0].MatrixIn * WtMatrix[0].WeightIn
|
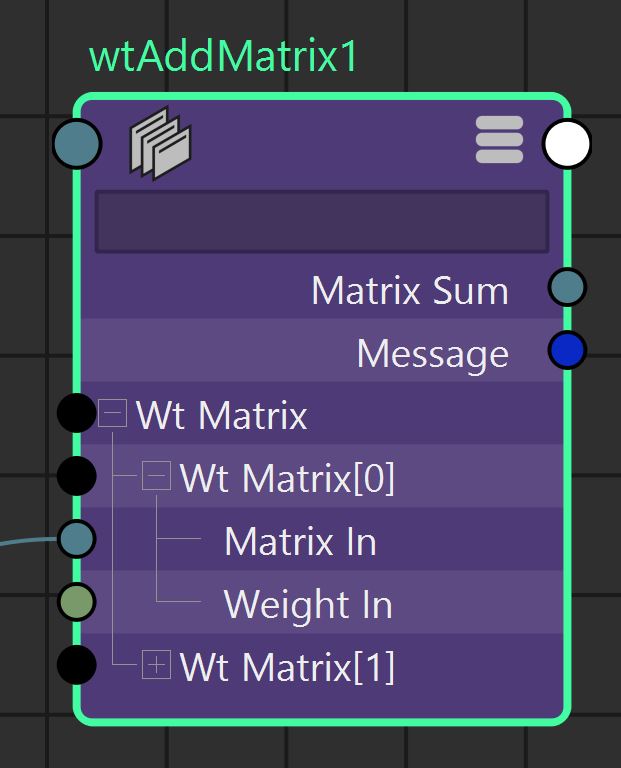 |
(From Maya 2024) For doubles see also: axisFromMatrix, translationFromMatrix, rotationFromMatrix, columnFromMatrix, rowFromMatrix.
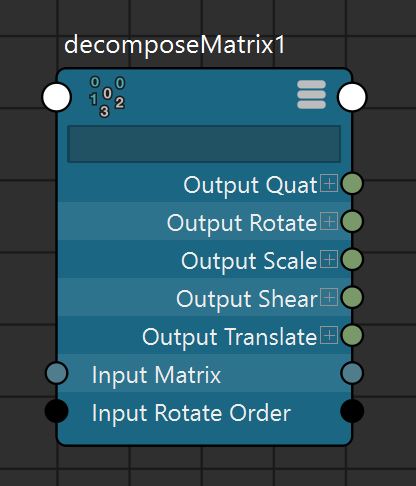 |
 |
  |
Extra nodes in 'matrixNodes.mll' plugin:
- inverseMatrix node
- transposeMatrix node
Plugins
https://github.com/serguei-k/maya-math-nodes (MIT license)
No comments
 Donate
Donate