Laplacian smoothing (C++ code to smooth a mesh)

Dropping a procedure to compute the Laplacian smoothing of a 3D mesh (with cotangent weights).
Note that the cotangent weights can be replaced by "w = 1.0f". In this case the smoothing will be said to be a "uniform Laplacian smoothing" and the initial distribution of the triangles will not be preserved. Of course you can test other barycentric weights.
Explicit Scheme
The code below use the "explicit scheme" to compute the Laplacian smoothing, which means we directly compute the new vertex position according to the previous position. Explicit scheme is known to be unstable (especially with cotangent weights) for 't > 1'. On the other hand the "Implicit scheme" (next section) of the Laplacian smoothing is unconditionally stable for any 't'! But you need to solve a linear system of equations
[ ![]() C++ code for the explicit and implicit scheme ].
C++ code for the explicit and implicit scheme ].
/// @brief Smoothing while minimizing the texture distortions.
class Weighted_laplacian {
// Some internal buffer for the computation
std::vector<Vec3> _buffer_vertices;
// Cache the cotangent weights
std::vector< std::vector<float> > _cotan_weights;
// Store the list of first ring neighbor for each vertex.
// the first ring neighbor is the list of vertices directly adjacent to another vertex
const Mesh_topology* _topo;
public:
/// @note avoid odd numbers of iterations they imply a full copy of
/// the vertex buffer at the end of the smoothing process.
int _nb_iter;
/// If the **rest** position of the mesh changes you need to update the
/// pre-computation step.
void update(const Mesh_topology& rest_pose_mesh)
{
_topo = &topo;
mesh_utils::laplacian_cotan_weights(topo, _cotan_weights);
}
// -------------------------------------------------------------------------
/// @param vertices : in place smoothing of this vertex buffer
void process(Vec3 vertices[],
float smooth_factors[],
int nb_vertices)
{
_buffer_vertices.resize( nb_vertices );
if(_nb_iter == 0){
return;
}
// first_ring[a_vertex][ith_neighbor of a_vertex] =
// "index of a neighbor directly connected to a_vertex"
const std::vector< std::vector< mesh_t::Vert_idx > >& first_ring = _topo->first_ring();
Vec3* src_vertices = vertices;
Vec3* dst_vertices = _buffer_vertices.data();
for(int k = 0; k < _nb_iter; k++)
{
for( int i = 0; i < nb_vertices; i++)
{
Vec3 cog(0.f);
float sum = 0.f;
size_t nb_neighs = first_ring[i].size();
for(size_t n = 0; n < nb_neighs; n++)
{
mesh_t::Vert_idx neigh = first_ring[i][n];
// Note: if we set w = 1.0f then the procedures operates
// an uniform smoothing, the initial distribution of
// the triangles will not be preserved
float w = _cotan_weights[i][n];
cog += src_vertices[neigh] * w;
sum += w;
}
// When using cotan weights smoothing may be unstable
// in this case we need to set t < 1
// sometimes you even need to get as low as t < 0.5
float t = smooth_factors[i];
dst_vertices[i] = (cog / sum) * t + src_vertices[i] * (1.f - t);
}
std::swap(dst_vertices, src_vertices);
}
if(_nb_iter%2 == 1)
utils::copy( vertices/*destination*/, _buffer_vertices.data()/*source*/, nb_vertices );
}
};
Implicit scheme
Laplacian smoothing can be seen has minimizing the mean-curvature. Recall that the mean-curvature normal is:
$$ \frac{\Delta p_i}{2} = -Hn $$
Which means the smoothing procedure we do in the above amounts to moving iteratively each vertex along the mean-curvature normal:
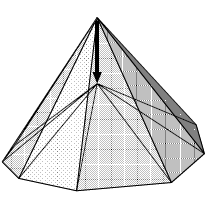
Implicit scheme
(draft notes)
Smooth a vertex:
$$
cog_i = \sum\limits_{{j \in \mathcal N(i)}} w_{ij} p_j
$$
Damping (linear interpolation with previous position) \( cog_i \lambda+ p_i (1-\lambda) \)
re-write the expression so that we add a displacement vector to the original vertex:
$$
\begin{array}{l}
cog_i \lambda+ p_i (1-\lambda) \\
cog_i \lambda+ p_i - p_i \lambda \\
p_i + cog_i \lambda - p_i \lambda \\
p_i + \lambda (cog_i - p_i) \\
\end{array}
$$
Let \( \mathbf{L} \) be the Laplacian matrix and define \( \tilde { \mathbf{L} }= \mathbf D_l^{-1} \mathbf L \) with \( \mathbf D_l \) the diagonal elements of \( \mathbf L \) and \( \mathbf V_k \) be the vertices after the k iteration of smoothing.
One iteration of Laplacian expressed with matrices:
$$
(\mathbf I +\lambda \tilde{ \mathbf L }) \mathbf V_k = \mathbf V_{k+1}
$$
This explicit scheme is unstable
Note: some authors chose to use \( -\mathbf L \) (positive diagonal, negative adjacent elements) then the expression becomes \( (\mathbf I - \lambda \tilde{ \mathbf L }) \mathbf V \)
You can precompute p iterations by multiplying the matrix to itself \( (\mathbf I +\lambda \tilde{ \mathbf L })^p \)
Now if you solve the linear system of equations:
$$
(\mathbf I - \lambda \tilde{ \mathbf L }) \mathbf V_k = \mathbf V_{k-1} \\
(\mathbf I - \lambda \tilde{ \mathbf L }) \mathbf X = \mathbf V
$$
this is unconditionally stable for any \( \lambda \) :) (i.e. no ugly mesh explosion)
Online slides and WebGL Demo of the implicit scheme smoothing (use keyboard arrows ➤ to navigate).
Related smoothing method
Reference:
Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow (Mathieu Desbrun & al)
Bonus
Mean curvature flow and pitfalls.
Curvature flow C++ implementation.
Conformal Willmore flow.
No comments
 Donate
Donate