Phong illumination model (cheat sheet)
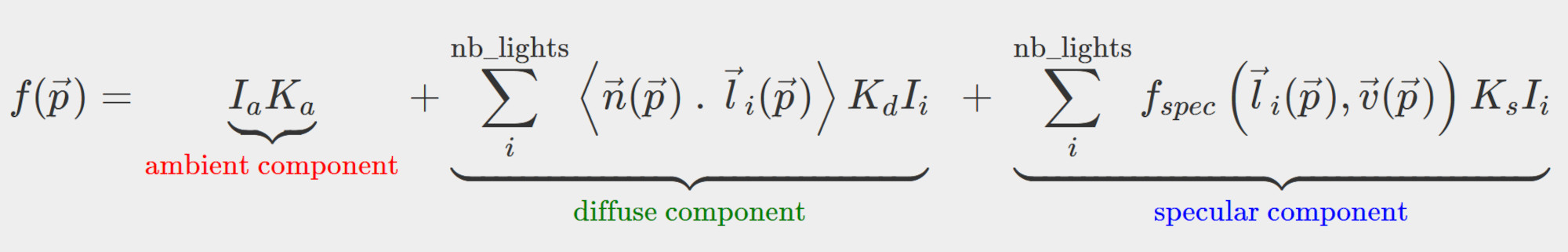
I summarize the Phong illumination model with the above equation and explain all the terms one by one.
French version:
[ ![]() pdf ]
[
pdf ]
[ ![]() odt ]
Eclairage de phong résumé
odt ]
Eclairage de phong résumé
\( \renewcommand{\vec}[1]{ \mathbf{#1} } \)
The function \(f:\mathbb{R}^3 \rightarrow \mathbb R\) takes a 3D point \( \vec p : (x,y,z)\) in input,
and returns a real number that represents the light intensity.
Point \( \vec p \) lies on the object's surface (i.e. where you'd like to compute the light intensity).
Note that this function is usually evaluated 3 times: for red, blue and green intensities.
This sheet only describes the computation for a single color channel.
Phong lighting is an extreme simplification of how lights really behaves, however, it is very efficient to compute. It decomposes the behavior of the light into 3 components: ambiant, diffuse and specular.
Ambiant component
In Phong lighting we don't simulate light bouncing in the scene, therefore, without any other treatment, parts of the object would stay black if not directly exposed to a light. To fix avoid this, objects are arbitrarily assigned a fixed intensity called the "ambient component". This intensity only depends on the material of the object and is assigned by the user
- \( I_a \) intensity of the scene (real number, user input)
- \( K_a \) intensity of the material (real number, user input)
Diffuse component (Lambertian diffusion)
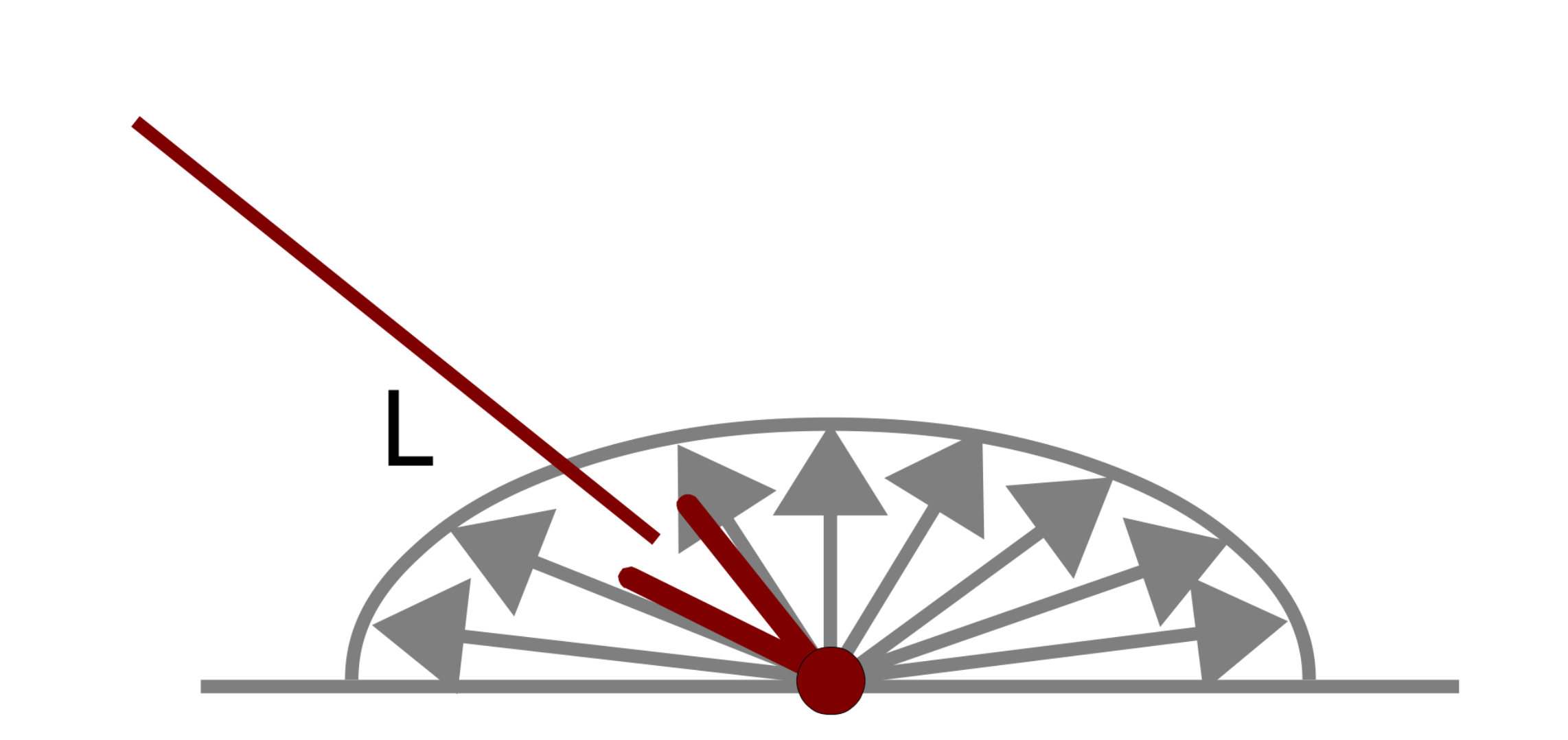
Simulate light that scatters uniformly when striking the object's surface (e.g. plaster material), the diffuse component intensity only depends on the input light direction. The intensity is independent from the viewing point since light is diffused uniformly from the object's surface.
- \( K_d \) diffuse intensity of the material (real number, user defined)
- \( I_i \) diffuse intensity of the ith light (real number, user defined)
- \( \vec n \) normal vector at the position \( \vec p \) on the object's surface (3D vector)
- \( \vec l_i \) direction of the light striking at \( \vec p \) (e.g. \( \vec l_i = \vec{lightPosition_i} - \vec p\)) (3D vector)
Specular component
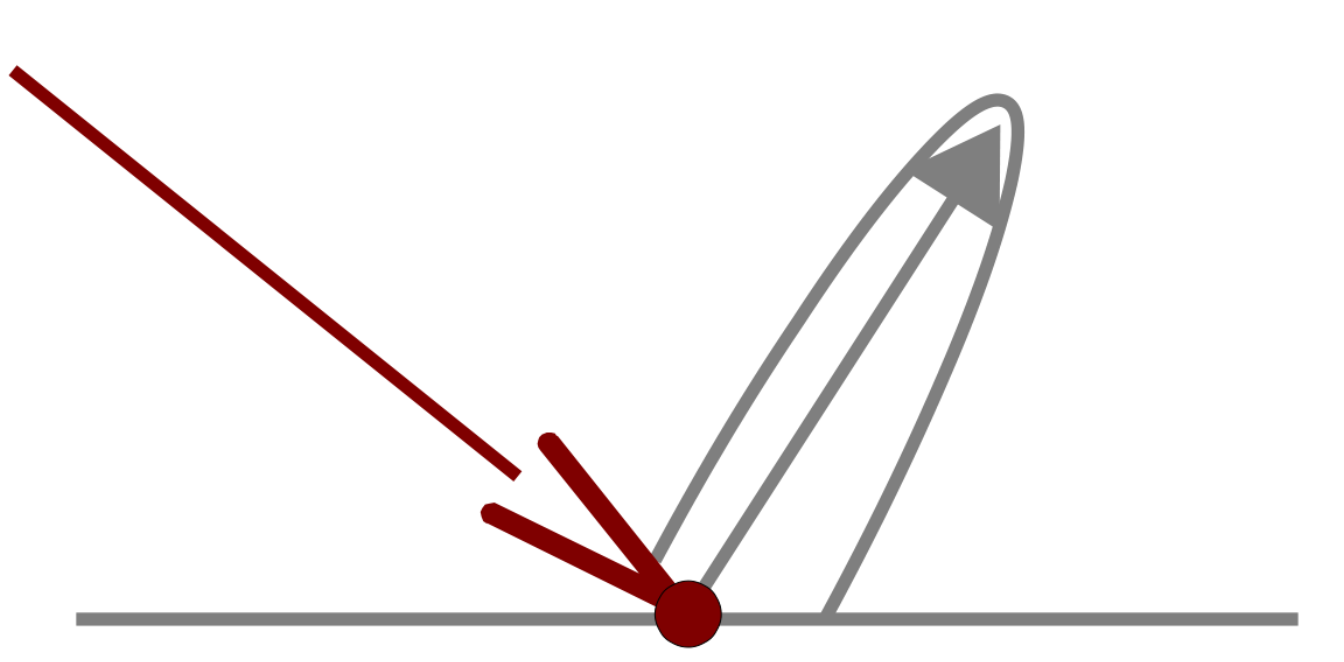
Simulate light that is reflected off the object, specular component depends on both the light source direction and viewing direction. (for instance, for a fixed light, a glossy material only displays some amount of reflection when viewed in at a specific angle)
- \( f_{spec}(\vec l_i( \vec p ), \vec v(\vec p)) \) specular term described below (real number)
- \( \vec v \) viewer direction (e.g. \( \vec v = \vec{cameraPosition} - \vec p\)) (3D vector)
- \(K_s\) specular intensity of the material (real number) (user input)
Two ways to compute the specular term \( f_{spec}(\vec l_i( \vec p ), \vec v(\vec p)) \)
1) Phong's specular term
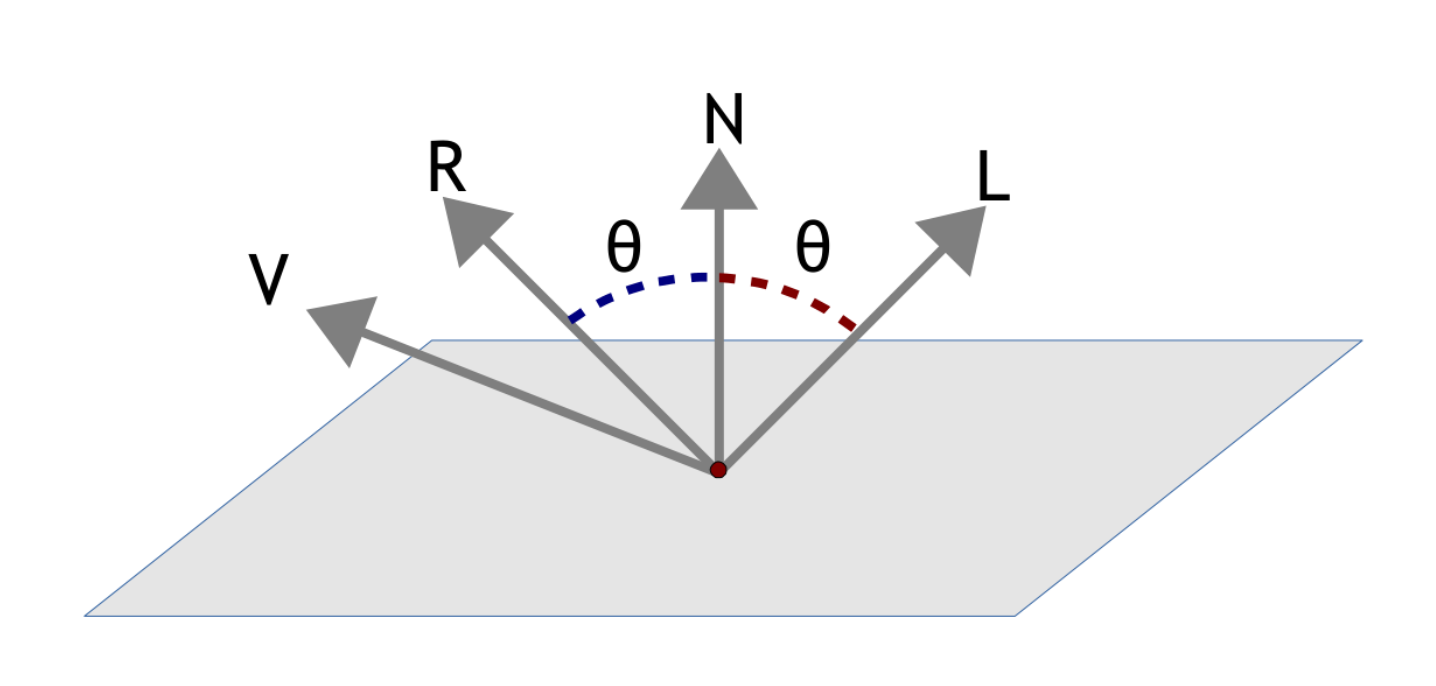
$$ \left \{ \begin{matrix} f_{spec} & = & (\vec r . \vec v)^c & \text{if } \vec r . \vec v > 0 \\ f_{spec} & = & 0 & \text{otherwise} \\ \end{matrix} \right.\ $$
Where \(c\) is coefficient representing the size of the specular reflection (user input) and \( \vec r \) is the reflection of the light vector \( \vec l \):
$$ \vec r = (2(\vec n . \vec l) \vec n) - \vec l $$
2) Jim Blinn's specular term
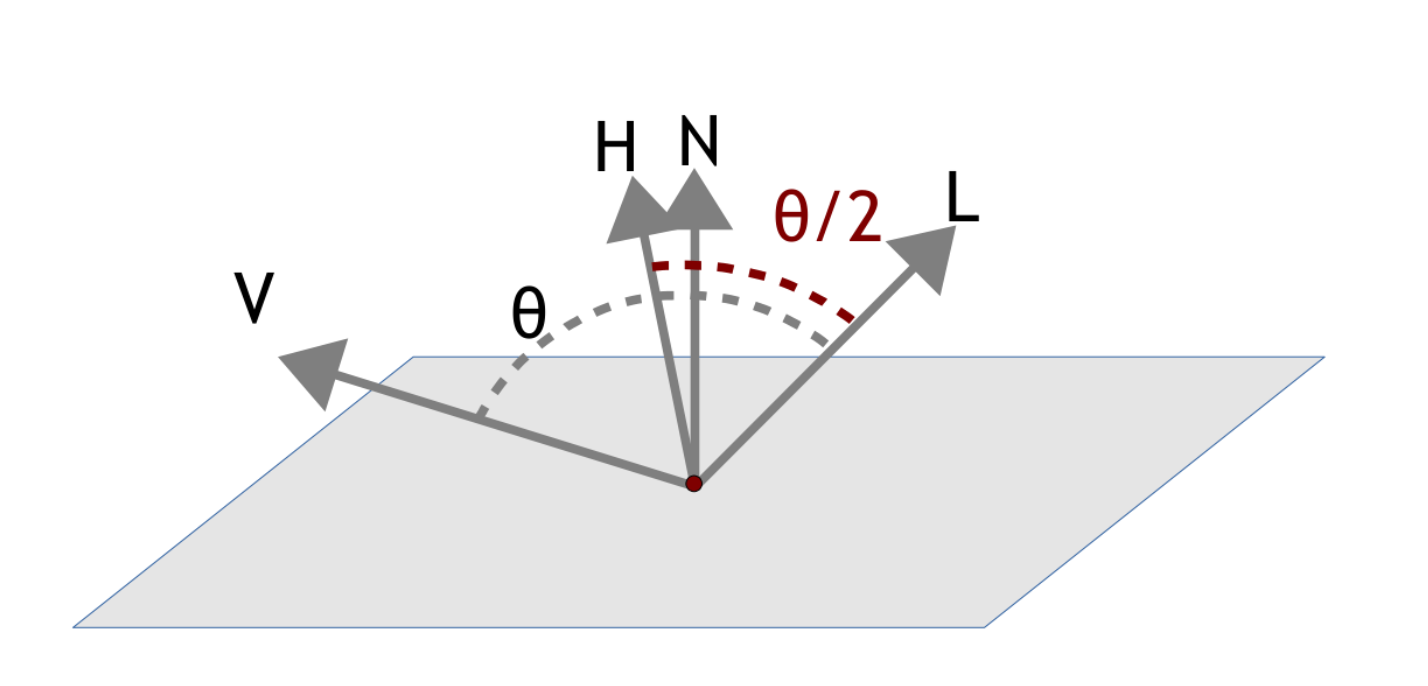
$$ f_{spec} = ( \vec n . \vec h)^c $$
Where \( \vec h \) is the bisector between \( l \) and \( \vec v \):
$$ \vec h = \frac{\vec l + \vec v}{ \| \vec l + \vec v \| }$$
References
One comment
 Donate
Donate
Thanks for the post. There is a typo: the reflection should be r=(2(n.l)n)−l.
Warren - 14/11/2019 -- 16:43Rodolphe: Oh right thanks for noticing!