Introduction to Jiggle physics and related mesh deformation

Who doesn't like jiggling! It's often needed to simulate loose or fatty parts of virtual characters or other blobby objects. I'll show you the basic steps to fake "soft body" or wobbly deformation. (Mainly we will be attaching vertices to springs...)
The first part of the tutorial will provide a ready to use "math recipe" to compute the jiggling of a single point. Then we'll work our way up to a full mesh animation and further explain the physic behind the hood.
A simple "jiggle" recipe
So, we would like to make a 3D point \( p_n \in \mathbb R^3\) at the \( n^{\text th} \) animation frame jiggle. One way to do this is to have a target point (\(target \in \mathbb R^3\)) which will attract \( p_n \) in such a way that it "jiggles" around his \( target \). We will also need the position of our point in the previous animation frame, that is, \( p_{n-1} \):

While being attracted by our target, our point is moving around and we can compute his velocity \( \vec{v_n} \):

When the target is not moving, the jiggling is supposed to slowly settle down to a rest position. Which means there must be some kind of opposing force, or a friction that makes our point stop at some point. We will model this drag force by making our point's velocity slow down as it travels towards our target. To this end, let's introduce a 'damping' factor: \( damping \in [0.0, 1.0]\). We'll multiply our velocity vector to shorten its length:

Applying the final velocity to \( p_n \) gives us an intermediate position \( p_n' \):
\( \vec v = (p_{n+1} - p_n ) . (1.0 - damping) \)
\( p_n' = p_n + \vec v \)

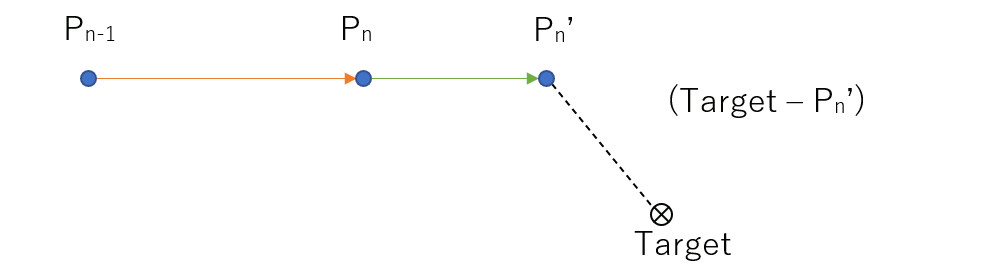
Alright! All is left to do is to apply the attraction force that \( target \) exerts onto \( p_n' \) to get the final position \( p_{n+1} \). The direction of the attraction is as follows:
\( \vec g = (target - p_n') \)
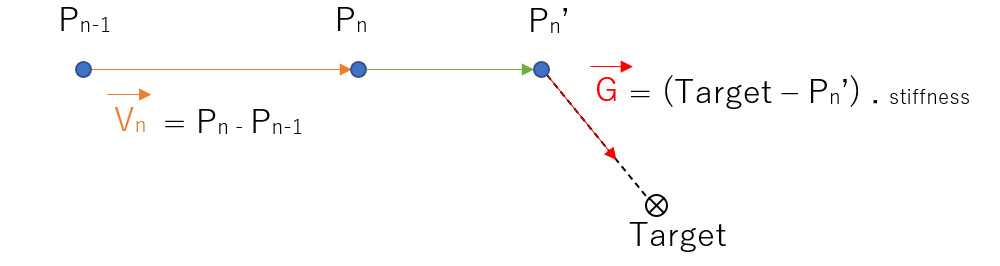
And we can modulate its strength using a 'stiffness' factor \( stiffness \in [0.0, 1.0]\):
\( \vec g = (target - p_n') . stiffness \)
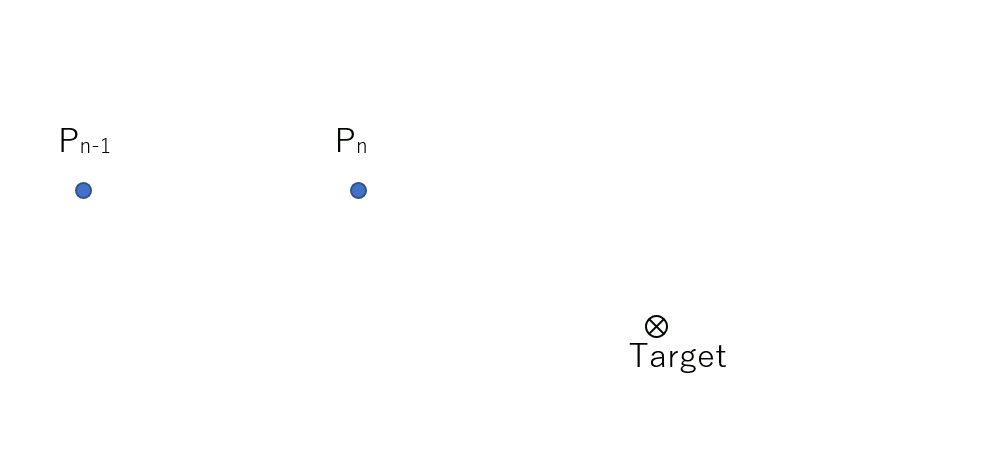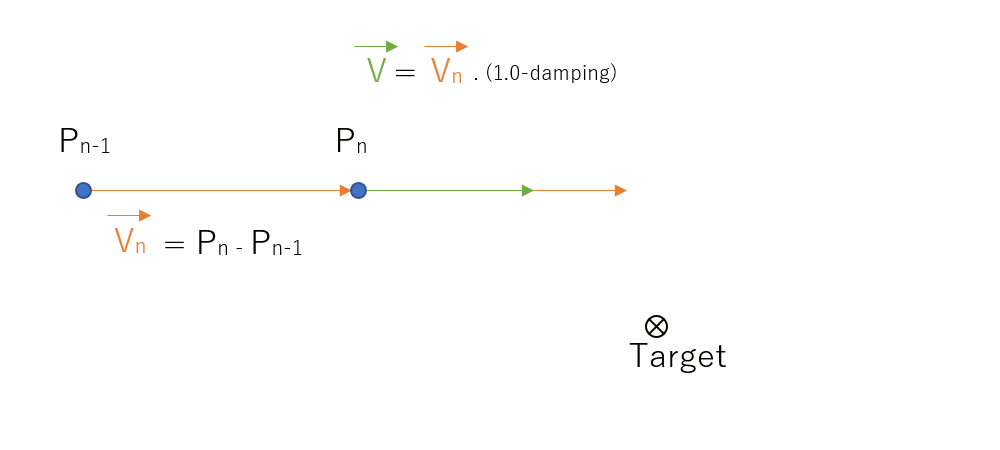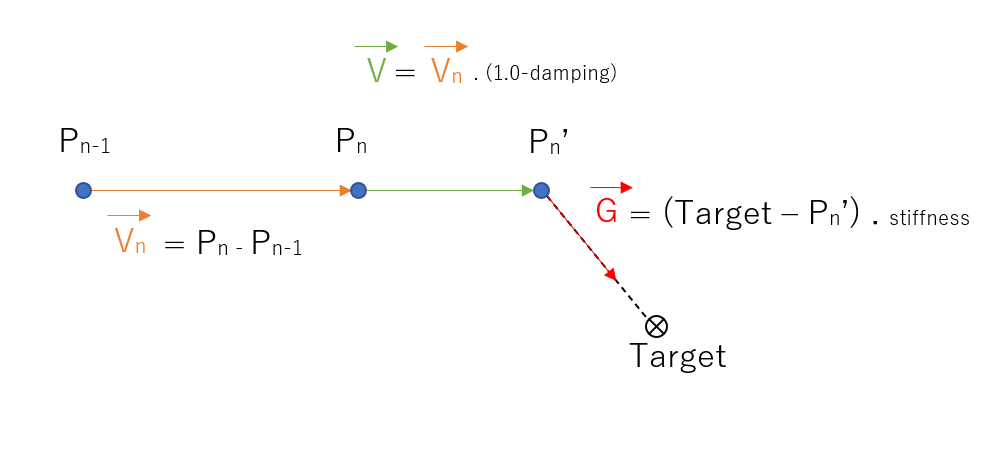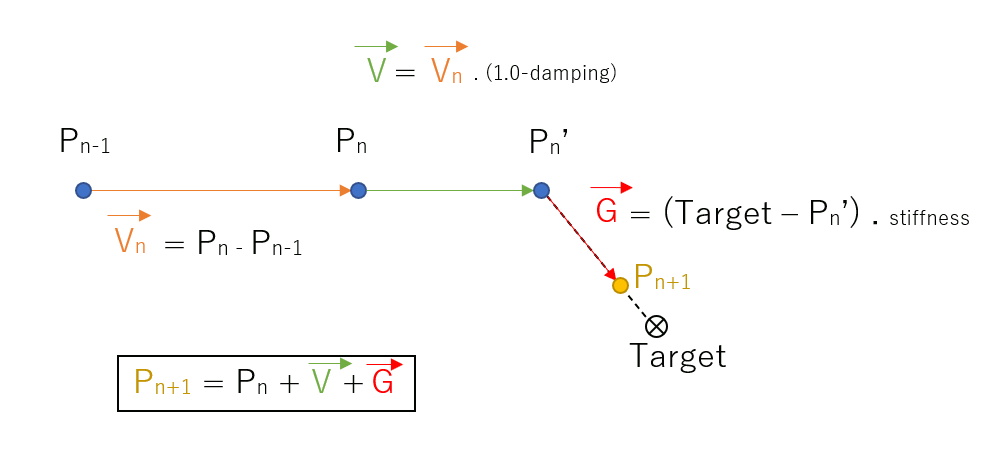
Which gives us the final position:
\( p_{n+1} = p_n + \vec v + \vec g \)
\( p_{n+1} = p_n + \vec v_n . (1.0 - damping)) + (target - (p_n + \vec v)) . stiffness \)
Recipe summary
Let's see this in action with the following webgl snippet:
Fiddle with the interactive code here! It was written with three JS and dat GUI. The core of the algorithm is as follows:
// The mesh representing our "target" (blue sphere)
let g_goalMesh;
// The grey and transparent sphere
let g_jiggleVertMesh;
let g_jiggleVertPrevious = new THREE.Vector3(0,0,0);
function getPosition( pos ) {
return new THREE.Vector3(pos.x, pos.y, pos.z);
}
function animate()
{
let damping = g_datGuiContext.damping;
let stifness = g_datGuiContext.stifness;
{
// Not handling time:
let currentPosition = getPosition( g_jiggleVertMesh.position );
let V = getPosition( g_jiggleVertMesh.position );
V.sub( g_jiggleVertPrevious );
V.multiplyScalar(1.0 - damping);
g_jiggleVertMesh.position.add( V );
let goal = getPosition( g_goalMesh.position );
goal.sub( g_jiggleVertMesh.position );
goal.multiplyScalar( stifness );
g_jiggleVertMesh.position.add( goal );
g_jiggleVertPrevious.copy( currentPosition );
}
requestAnimationFrame(animate);
g_renderer.render(g_scene, g_camera);
}
Jiggle a whole mesh
Here is how we are going to extend the jiggling of a single point to an entire mesh. We are going to maintain two sets of positions:
- Jiggling vertices
- Base vertices
"Jiggling vertices" are simply the positions describing the final animation, so we use this set to display the final mesh. "Base vertices" will serve as the set of goal positions associated to each "jiggling vertices". The base vertices are simply the position of the mesh after a simple transformation such as translation, rotation or scale of the mesh. We won't display the base vertices.
In our JavaScript widget we explore four options:
1) User transform (base vertices)
Mainly because I'd like to show what's happening under the hood,
we ignore jiggling vertices and only display the base vertices. We just apply the user transformation (when we grab the object with the mouse) to the mesh.
2) Jiggle all vertices
Let's now try to make the mesh jiggle. Every vertices are considered to be "jiggling vertices" and follow the base vertices which we hide now.
Well, the problem is while the object somewhat jiggles it does it in a monolithical manner.
3) Jiggle a subset of vertices Here we only select a subset of "jiggling vertices" where we apply the jiggling algorithm, the rest of the vertices are kept as the "base vertices". The jiggling is now local but it still moves as one block...
4) Jiggle map: weighted subset To avoid the above issues we need to introduce the "jiggle map". For each vertex we now associate a weight ranging between \( [0.0- 1.0] \) that defines the amount of jiggling. Based on the jiggle map, we will interpolate between the "base vertices" \( p_i \) and "jiggling vertices" \( j_i \):
\( finalPosition_i = p_i (1.0 - jiggleMap[i]) + j_i . jiggleMap[i]\)
todo find a small mesh to accelerate computation. color per vertex to show the jiggling map.
Time integration
You may have noticed that, so far, we don't take into account time.
Every time we compute a new position, we ignore how much time it took between two subsequent calls of the animate() function.
This means our simulation is dependent on the refresh rate.
The above is simple and works fine, but, only if a constant amount of time lapses between each frame.
In the new sections I'll show case some alternatives to take time into account.
To this end, we need to properly implement the so called "time integration".
Beyond the recipe
Explicit Verlet time integration:
\( x^{t+1} = x^t + v^t \Delta t + f(x^t) \frac{\Delta t^2}{m} \) \( v^{t+1} = \frac{x^{t+1} - x^t}{\Delta t} \)
Spring force:
\( f_s = \frac{(x_j - x_i)}{\| x_j - x_i \| } \left [ k_s ( \| x_j - x_i \| - l_0) \right ] \) \( f_d = \frac{(x_j - x_i)}{\| x_j - x_i \| } \left [ k_d (v_j - v_i) . \frac{(x_j - x_i)}{\| x_j - x_i \|} \right ] \) f=fs-fd \( \vec g = f_s = k_s (target - x_i) \) \( f_d = \frac{(target - x_i)}{\| target - x_i \| } k_d (v_{target} - v_i) . \frac{(target - x_i)}{\| target - x_i \|} \)
Recall that large time step are unstable with any "explicit" integration scheme such as explicit Euleur or explicit Verlet. One option is to cap frame-rate for the simulation and only a fixed refresh rate of the physic simulation when fps is too high. As for when fps is too low you will get in trouble (or you can decompose simulation into sub steps which will be even slower...) compare with cloth sim tutorial (mos garden) the integration scheme and see if it was explicit Verlet
Recipe variations
1) Original recipe:
\[ p_{n+1} = p_n + \vec v_n . (1.0 - damping)) + (target - (p_n + \vec v)) . stifness \] \[ p_{n+1} = p_n + \vec v_n . (1.0 - damping)) + (target - p_n') . stifness \]2) Attract current point instead of predicted position:
\[ p_{n+1} = p_n + \vec v_n . (1.0 - damping)) + (target - p_n) . stifness \] TODO:3) Accounting for time and mass in a Verlet like manner \( \vec g = (target - p_n) \):
\( p_{n+1} = p_n + \frac { (p_{n+1} - p_n ) } {\Delta t} . \Delta t . (1.0 - damping)) + (target - (p_n + \vec v)) . stifness .\frac{ {\Delta t}^2}{m} \) \( p_{n+1} = p_n + \vec v_n . (1.0 - damping)) + (target - (p_n + \vec v)) . stifness .\frac{ {\Delta t}^2}{m} \)\( p_{n+1} = p_n + \vec v + \vec g .\frac{ {\Delta t}^2}{m} \) (for large time steps simulation explodes... todo write the problematic parameters)
4) Explicit Verlet, Truly represent spring force (length zero) and dampness with Verlet (just like in Muller's course):
5) Explicit Verlet, Spring of length zero but damping is just a counter vector to the point's velocity
Jiggle point everything:
Time integration: explicit Verlet It's a spring with length zero.
No comments
 Donate
Donate