Tensor basic definition

This post considers you have have prior knowledge about: matrix, matrix multiplication, vector matrix operations, representing transformations and such.
Introduction
This aims to explain what tensors are, using various degrees of difficulty. The topic is difficult, and there is no straightforward way to give a single and easy to understand definition for everyone. Tensors are used in many fields, such as, Neural Networks, Continuum Mechanics or even General Relativity; and while tensors are a quite general concept, depending on which field you apply them, you may come across very different definitions. This is often the cause of a great deal of confusion.
Let's take the concept of vectors as an example of a mathematical object that can be interpreted or used in various ways. In statistics, a vector may just represent 2 real numbers storing some data (e.g. height and age). In geometry, it might represent 2 or 3 coordinates (x,y,z), and in abstract algebra (i.e. vector spaces) the definition gets much more involved, general and well abstract.
Ultimately, the strict mathematical definition of a tensor is hard to grasp and requires many background knowledge, such as, linear algebra, abstract algebra and vector spaces in particular. But when used in a specific scenario, you may only be aware of a simplified version of what a tensor really is. Back to the vector analogy, if all you do, is work on 2D geometry, then a vector only needs to be 2 real values interpreted as the distance from the x and y axis of some Cartesian coordinate system. Hopefully, since I give various definitions, regardless of your current mathematical proficiency, this note will give you some idea of what a tensor is.
Note: screenshots were taken from youtube videos linked at the end of the article.
Easy but incomplete definition
I - Tensor = multi-dimensional array of numbers
A tensor is often viewed as a generalized matrix. That is, it could be a 1-D matrix (i.e. a vector), a 3-D matrix (a cube of numbers), a 0-D matrix (a single number), or a higher dimensional structure that is harder to visualize.
The 'n' of n-D in this case is called the order, degree or rank of the tensor (we'll use rank here). So while \(n\) is the rank of the tensor and tells you how many indices are used in this array of numbers, its dimension actually relates to its number of elements
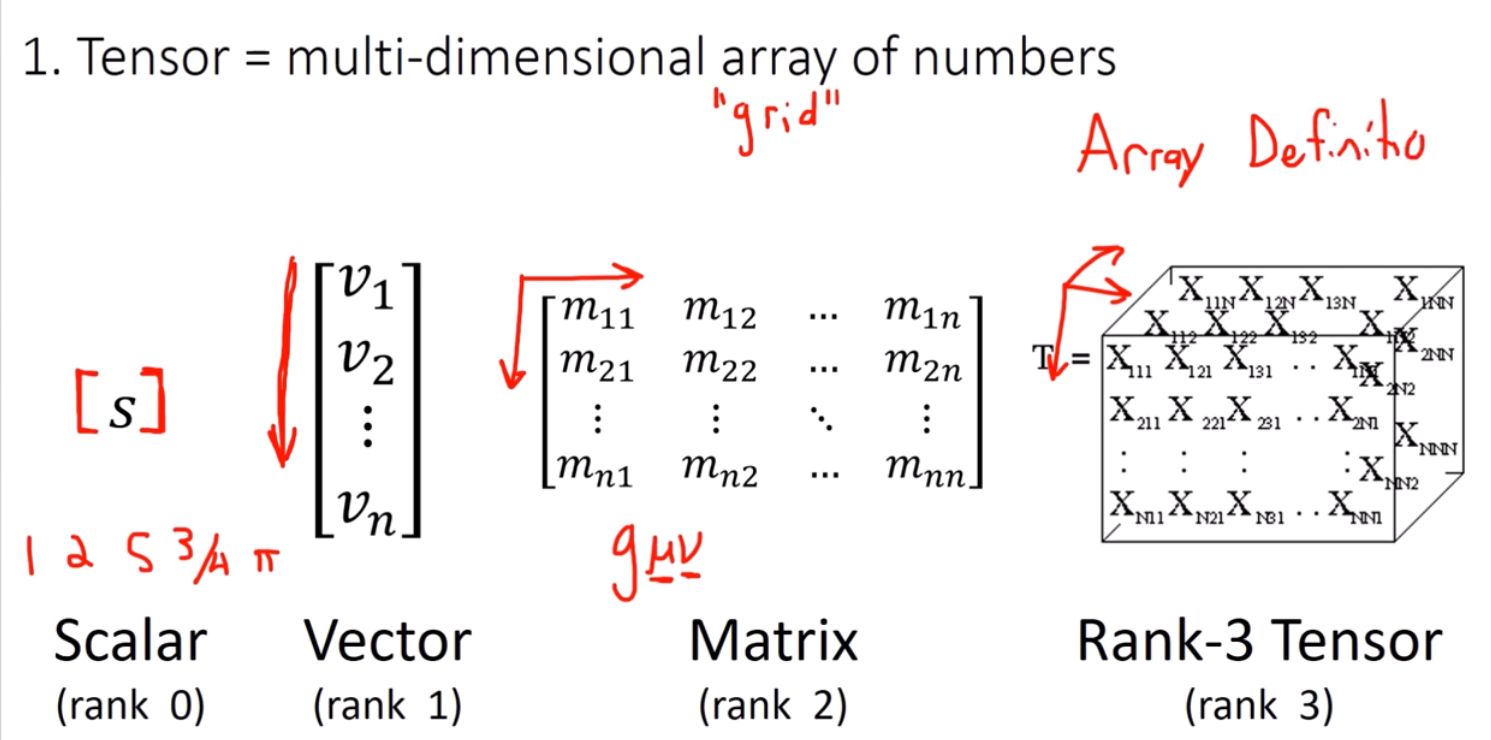
A word of caution: this is a seriously limited and oversimplified definition. And we will build on it. However, it is enough to understand what are tensors when used in the context of neural networks, as in this field they are mostly viewed as mere multidimensional array of data such as vectors, matrices etc.
Examples of rank 2 tensors
Electromagnetic tensor:
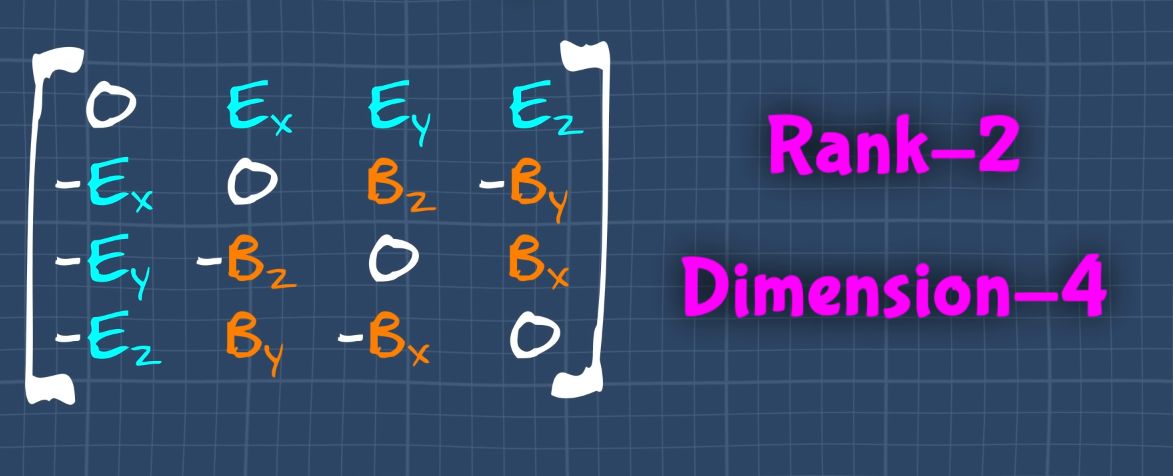
Stress tensor:
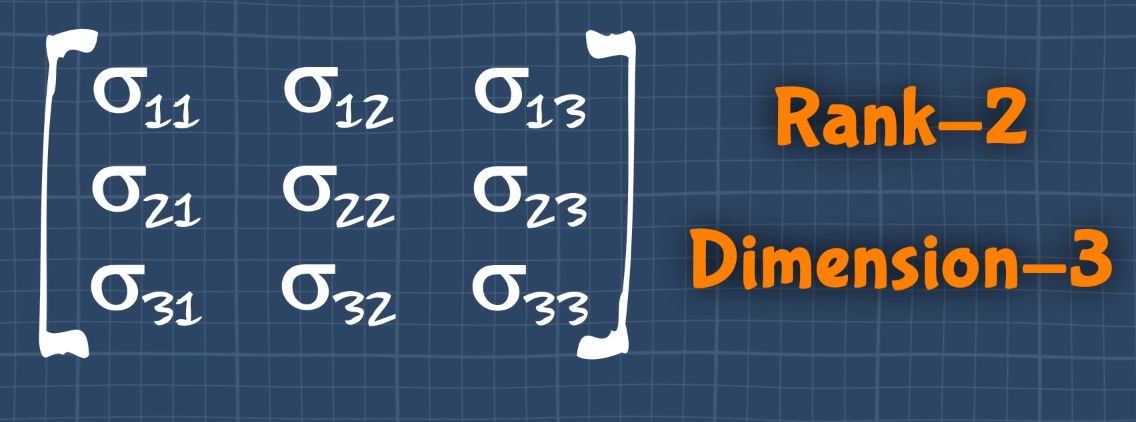
Rank 3, dimension - 3 (i.e 3 elements along the rows and columns)

Rank 4

Index notation
Each element (number) position in the tensor can be described using indices:
- Rank-0: \( \tau \), a scalar
- Rank-1: \( \tau_i \), a vector
- Rank-2: \( \tau_{ij} \), a matrix (Latin letters for Dimension-2/3)
\( \tau_{\alpha\beta} \) (Greek letters for Dimension-4) - Rank-3: \( \tau_{ijk} \), a cube of matrices.
- Rank-4: \( \tau_{ijkl} \), an array of cubes
- ...
3D Stress tensor
So far in our description it might be hard to see why we need to call this a "tensor", why not just call it a matrix or a multidimensional array of numbers?
Well, one reason is that when use the term "Tensor", the terminology indicates us how to interpret this object and what rules should apply (what operations are allowed). To be a bit more concrete: this difference is somewhat similar to calling "3D vector" what we could simply describe as a "3x1 matrix". While a 3x1 matrix is just a generic array of numbers (it could represent temperatures in 3 different cities), when using the term "vector" in the context of geometry we usually expect it to represent a direction in space.
So, when used in the context of physics like continuum mechanics, "tensor" is a specific terminology that usually designate a 3x3 matrix representing tensile forces and with specific expectations on how they behave regarding changes of coordinate systems.
Let's see a concrete example of a rank-2 tensor, the "stress tensor". Somewhat similar to a transformation matrices, stress tensors will store a stress force at each row of the tensor (i.e. 3x3 matrix), We will name those stress forces \( \vec X \), \( \vec Y \) and \( \vec Z \):
\[ T_{ij} = \begin{bmatrix} \vec X \\ \vec Y \\ \vec Z \\ \end{bmatrix} = \begin{bmatrix} X_x & X_y & X_z \\ Y_x & Y_y & Y_z \\ Z_x & Z_y & Z_z \\ \end{bmatrix} \]The stress forces represent the 3 stresses applied to the faces of a unit cube:


There is one force for each orientation of the cube (x,y and z). This unit cube is often used to represent the local stress force at some specific point of a larger material:

Now what's particularly convenient with the stress Tensor \(T_{ij}\), is that not only each row provides the stress force along x, y and z directions, but we can infer the stress along any arbitrary direction \( \vec v \). To do so we simply multiply the stress tensor by the desired direction:
\[ \vec v . T_{ij} \]In the case of our steel beam earlier we can slice it in a particular direction and infer the stress applied in the direction of that slice:

Interestingly you can visualize the resulting stress forces by multiplying by every possible orientation, this give you a stress field:

Original animated explanations: Stress tensor visualization video
note: a property of the stress force applied to a material in state of static equilibrium (not moving or deforming), is that the unit cube should stay at equilibrium as well. This means the cube should not move rotate or otherwise deform if we consider all forces applied to it, they should all compensate each other (as Newton's 3rd law dictates). It results from that fact that the matrix representing a stress tensor should always be symmetrical.
II - Invariant under coordinate change
A better, more complete definition of a tensor is, that a tensor is not just a multidimensional array of numbers,
it also has to be invariant under any change of coordinates.
This rule means we should always be able to transform a tensor \(T\) to some other coordinate system
so that the transformation \(T'\) still represents the same tensor. For instance the velocity vector
should still point towards the same object whether we express its coordinates from some some place or another.
Likewise, we expect a stress tensor to deform an object the same way no matter the coordinate system we use to
express it.
Illustration:
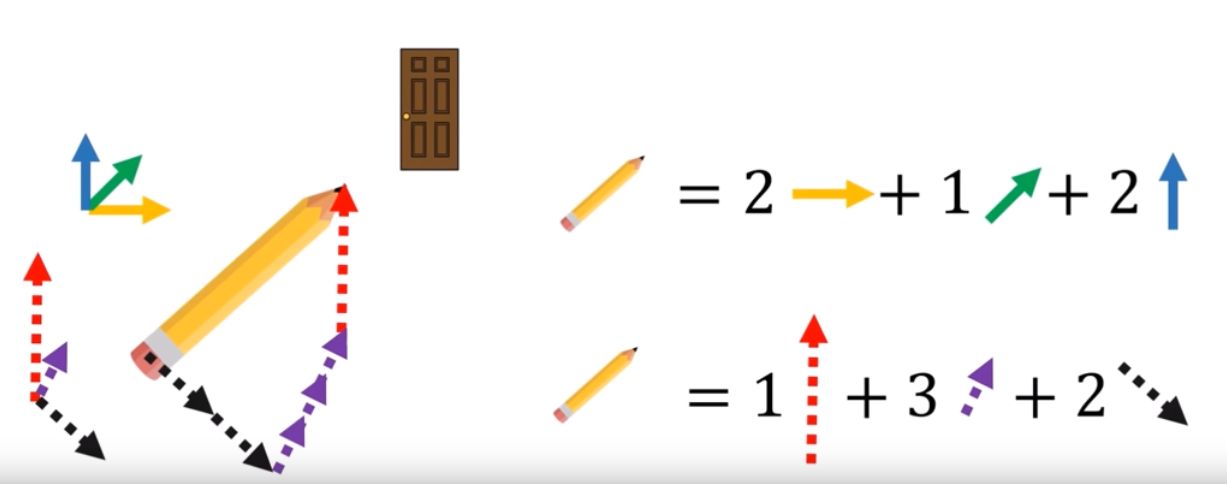
Regardless of the coordinate system the pencil always points to the door with the same length. We can transform components with forward or backward transformations. (Note: if the vector/tensor becomes null under specific coordinate systems then we call it a pseudo-vector/tensor)
III - Descriptive definition:
If wanted to summarize our explanation of a tensor so far we would say:
A 'rank-n' tensor in 'm-dimensions' is a mathematical object that has \(n\) indices and \(m^n\) components and obeys certain transformation rules.
alternatively:
A tensor is a geometric object (vector, 3D reference frame) which is expressed and transformed according to a coordinate system defined by the user.
IV- Alternate definitions
Alternate interpretation: Tensors as partial derivatives and gradients that transform with the Jacobian Matrix
Strict mathematical definition
This is the most rigorous and general definition, it's also the hardest.
A type \((p,q)\) tensor \(T\) is defined as a multi-linear map (wiki definition):
$$ T: \underbrace{ V^* \times \cdots \times V^*}_{p \text{ copies}} \times \underbrace{ V \times \cdots \times V}_{q \text{ copies}} \rightarrow \mathbb F $$Where \(V\) is a vector space (also called linear space) over a field $\mathbb F$ , and \(V^*\) is its corresponding dual space (blog post of dual space). (Note that while $\mathbb F$ is oftentimes the set of real numbers $\mathbb R$, it could well be the rationals $\mathbb Q$ or complex numbers $\mathbb C$)
The literal way of saying the above is:
Tensor is a collection of vectors and covectors
combined together using the tensor product.
Explained here, is perhaps the most concise way to summarize the mathematical definition:
tensor = multilinear F function.
In the case of reals:
tensor = multilinear Real function.
In most field you may not need to fully grasp this definition, especially if all you do is just applied some specific kind of tensor. It all depends how deep and far you want to go with this tool.
So to understand this definition you would first need to know and understand what is a "multi-linear map" \(f(\cdot,\cdot,\cdots)\). Which means you need a background in linear algebra to understand what is a "linear map" \(f(\cdot)\) in the first place. Material like the series "essence of linear algebra" by 3blue1brown does a wonderful job to explain the topic. In particular, the fact that a vector or a matrix can be viewed as a linear map \(f(\cdot)\) should be "evident" or "easy" for you before thinking about diving into this high level and abstract version of tensor calculus. A foundation about abstract algebra (a.k.a group theory) and especially vector spaces is essential as well. Introduction to group theory, or this series on abstract algebra can be a great start.
You may also want to look into tensor product as this notion is tied with tensors
References
Good starter explanation
What the HECK is a Tensor?!?, The Science Asylum
(Physics / transformation invariant explanation)
Associated material (it has a chapter on tensors)
Tensors for Beginners, eigenchris
(Progressive series, from easy definition at the beginning building up to more challenging ones)
Tensor Calculus, Faculty of Khan
Others (less fan):
Dan Fleisch's take
Tensors Explained Intuitively: Covariant, Contravariant, Rank
Les Tenseurs Pour les Débutants. (french) (Purely computational, descriptive explanation)
More strict definitions:
- What a tensor really is (French)- Mais c'est quoi un tenseur ? (French)
Associated pdf: cours_tenseurs_ups.pdf
- "Mécanique des milieux continus" Tome I "Concepts généraux" Jean Salençon (page 303)
No comments
 Donate
Donate