Compute B-Spline Basis functions with Cox-de Boor recursion

Math, JavaScript ThreeJs, python to compute B-spline basis functions with De Boor's algorithm - 09/2023 - #Geometry

for $n+1$ points:

$$p(u) = \sum_{i=0}^n N_i^k(u) P_i$$

$k$ is the order of the spline (number of influencing points) contrary to Bézier notations the degree is $k-1$

$$N_i^k(u) = \frac{u - u_i}{u_{i+k-1} - u_i} N_i^{k-1}(u) + \frac{ u_{i+k}- u}{u_{i+k}-u_{i+1}} N_{i+1}^{k-1}(u)$$ $$N_i^1(u) = \left \{ \begin{aligned} 1 & , & u_i \leqslant u < u_{i+1} \\ 0 & , & \text{otherwise}\\ \end{aligned} \right .$$

knot vector $\vec u \in \mathbb R^{k+n+1}$: $\{u_0, \cdots, u_{i}, \cdots, u_{k+n}\}$ where $u_i \leq u_{i+1}$ must be guaranteed.

Note that the stop condition for the recursion is also sometimes written as follows:

$$ \require{cases} N_i^1(u) = \begin{cases} 1/2 & u_i\leq u < u_{i+1} \\ 0 & \text{else} \end{cases} + \begin{cases} 1/2 & u_i< u\leq u_{i+1} \\ 0 & \text{else}\end{cases} $$

Here is also another neat way to express the recursive expression, where linear interpolation is exposed:

$$ N_{i}^{k} = \quad \omega_{ik} \ N_{i}^{k-1}(u) \quad + \quad (1-\omega_{i+1,k}) \ N_{i+1}^{k-1}(u), \\ \omega_{ik}(u) = \frac{u-u_i}{u_{i+k-1}-u_i} $$

Three JS app

2D view:

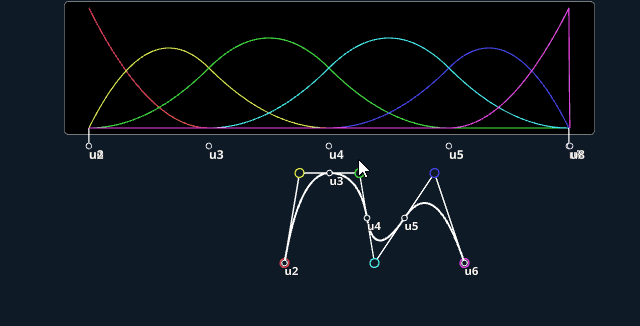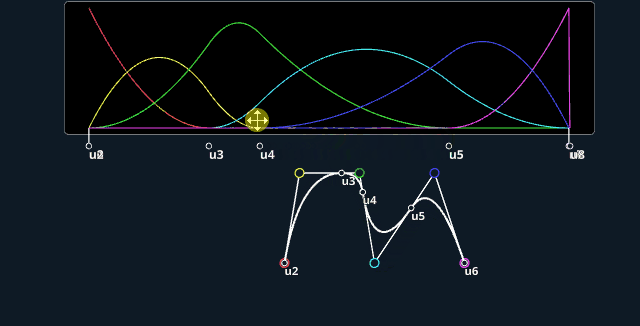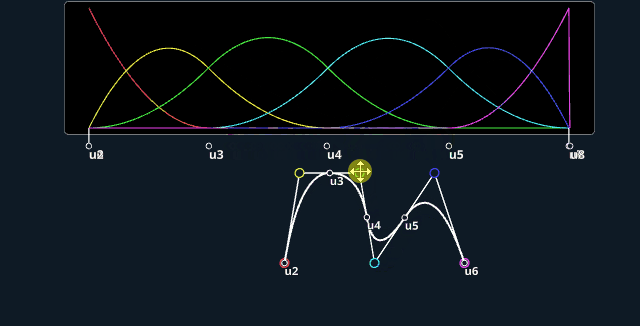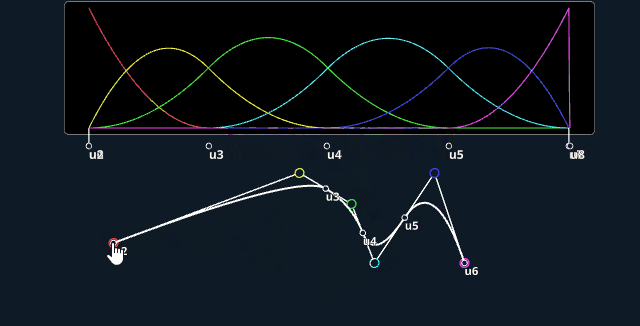
3D also available:

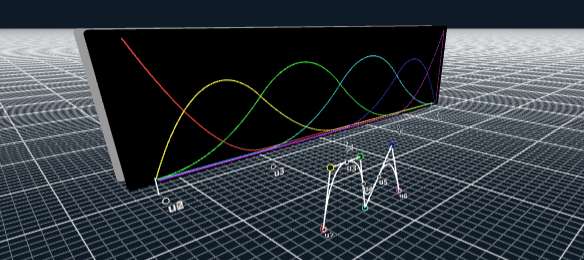
Live application

The applet below directly inspired by the amazing video of Freya Holmér on "The Continuity of Splines". I wanted to reproduce the styling which I thought was cool, and play myself with the various parameters.

Wheel: zoom in/out
Left click: select curve's control points and knots of the basis function!
Right click: pan

[

Go to source code ]

Code Pen

You can also play with a simplified version on CodePen

"use strict";

import * as THREE from "https://cdn.jsdelivr.net/npm/three@0.114/build/three.module.js";
import { OrbitControls } from "https://cdn.jsdelivr.net/npm/three@0.114/examples/jsm/controls/OrbitControls.js";
import { DragControls } from "https://cdn.jsdelivr.net/npm/three@0.114/examples/jsm/controls/DragControls.js";


const g_canvasName      = document.querySelector("script[type=module]").attributes['canvas_name'].value;
const g_canvaContainer  = document.getElementById(g_canvasName);
const g_canvasRootDiv   = document.getElementById("threeJsWrap_" + g_canvasName);
const g_datGuiInnerDiv  = document.getElementById("datGuiInner_" + g_canvasName);
const g_datGuiBottomDiv = document.getElementById("datGuiBottom_" + g_canvasName);

/*
    TODO: draw knots on the curve.
    TODO: ability to manually edit knot values.
    FIXME: order 1 for t = t_max does not properly interpolate last point. (null point)
*/


/*
function windowWidth() { return window.innerWidth;  }
function windowHeight(){ return window.innerHeight; }
*/
function windowWidth() { return g_canvaContainer.clientWidth;  }
function windowHeight(){ return g_canvaContainer.clientHeight; }

// for debugging purposes we allow switching backto perspective:
let g_orthographic = true; 

// ------------------------------------------------------------------------
// 
// ------------------------------------------------------------------------

let g_camera;
let g_scene;
let g_draggableObjects = [];
let g_dragControls = null;
let g_renderer;
let g_controls;

// ------------------------------------------------------------------------
// Dat GUI setup
// ------------------------------------------------------------------------

let g_datGuiContext =  {
    camera:  "Orthographic",
    nbPoints: 6,
    order: 5,
    knot_type: "open_uniform",
};

// callback when the html page finish loading:
window.onload = function () {
    //return;     
    setValue();        
    var gui = new dat.GUI({ autoPlace: false, width: () => windowWidth() });  //    
    g_datGuiBottomDiv.appendChild(gui.domElement);

    
    
    //gui.add(g_datGuiContext, 'camera', ["Orthographic", "Perspective"]).onChange(setValue);
    gui.add(g_datGuiContext, 'knot_type', ["open_uniform", "uniform", "custom"]).name("Knot type:").onChange(
        () => {
            g_bspline.knot_type = g_datGuiContext.knot_type;
            if(g_bspline.knot_type == "custom")
            {
                // make sure nb_points + order = knots.length
                setNbpPointsCallback(6);
                setOrderCallback(5);
                g_bspline.set_custom_knots([0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 2.0, 2.0, 2.0, 2.0, 2.1]);
            }

            g_bspline.update();
            g_bspline_mesh.updateSplineCurve();
            g_basis_mesh.updateBasisFunc();
        }
    );

    let nbPointsSlider = gui.add(g_datGuiContext, 'nbPoints', 2, 20, 2)
    nbPointsSlider.onChange(
        () => { 
            setNbpPointsCallback( Math.ceil(g_datGuiContext.nbPoints) );            
        }
    )
    // updates slider when g_datGuiContext.nbPoints is changed by other means
    nbPointsSlider.listen();

    let orderSlider = gui.add(g_datGuiContext, 'order', 1, 9, 2)
    orderSlider.onChange(
        () => {
            setOrderCallback( Math.ceil(g_datGuiContext.order) );             
        }
    );
    orderSlider.listen();


    //document.getElementById("myCanvas").style.zIndex = "-1";  
    //g_canvaContainer.appendChild(gui.domElement);

};

function setNbpPointsCallback(nb){
    g_dragControls.dispose();
    g_draggableObjects = [];
    if( g_bspline.order > nb ){
        g_datGuiContext.order = nb;
        setOrderCallback( nb );
    } 

    g_bspline.setNbpPoints( nb );
    meshSetup(g_scene, g_draggableObjects);
    g_dragControls = createDragControl();  
}

function setOrderCallback(order){
    g_dragControls.dispose();
    g_draggableObjects = [];

    if( order > g_bspline.nbPoints() ){
        g_datGuiContext.nbPoints = order;
        setNbpPointsCallback( order );
    }

    g_bspline.order = order;    
    meshSetup(g_scene, g_draggableObjects);

    g_dragControls = createDragControl(); 
}

function setValue() {    
    //d_light.color.setHex( g_datGuiContext.lightColor1 );  
    //h_light.color.setHex( g_datGuiContext.lightColor2 );
}

// ------------------------------------------------------------------------
// Camera parameters
// ------------------------------------------------------------------------

let g_cam_params = {    
    orthographic: g_orthographic,
    aspect_ratio() { return windowWidth() / windowHeight(); },
    left() { return this.frustumSize * this.aspect_ratio() * (-0.5); },
    right() { return this.frustumSize * this.aspect_ratio() * 0.5; },
    top() { return this.frustumSize * 0.5; },
    bottom() { return this.frustumSize * (-0.5); }, //
    near: 1,
    far: 1000,
    frustumSize: 50,
    
    // Update ThreeJS camera with current window parameters
    update(camera){
        camera.left = this.left();
        camera.right = this.right();
        camera.top = this.top();
        camera.bottom = this.bottom();
        camera.aspect = this.aspect_ratio();
        camera.updateProjectionMatrix();
    },
        
    createThreeJsCamera(){
        if (!this.orthographic) {  //
            return new THREE.PerspectiveCamera(60, this.aspect_ratio(), this.near, this.far);
        } else {
            return new THREE.OrthographicCamera( this.left(), this.right(), this.top(), this.bottom(), this.near, this.far);
        }        
    },
};

// -----------------------------------------------------------------------------


let g_bspline = 
{
    resolution: 500, // how much segments to render the curve
    order: 5,       // number of influencing points (degree = order -1)
    ctrlPointInitList: [
        new THREE.Vector3(-5, -5, 0),
        new THREE.Vector3(-2,  5, 0),
        new THREE.Vector3( 2,  5, 0),
        new THREE.Vector3( 5, -5, 0),
        new THREE.Vector3( 7,  5, 0),
        new THREE.Vector3( 9, -5, 0), 
    ],
    knots:[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 2.0, 2.0, 2.0, 2.0, 2.1], /* size = order + nb control points */
    knot_type: "open_uniform", // "uniform" "open_uniform" "custom"

    // Inefficient Cox-de Boor recursion to compute the basis function of 
    // our B-spline curve.
    basis(k/*order*/, i/* ctrl point index */, t/*float parameter*/)
    {           
        console.assert( k >= 1 );
        console.assert( i >= 0 );       

        if(k == 1){
            /* 
               We could use if( this.knots[i] <= t && t <= this.knots[i+1] ) (none strict inequality) 
               with open uniform knot vector 
            */    
                        
            let inRange = ( this.knots[i] <= t && t < this.knots[i+1]  );                
            if( inRange)
                return 1.0;
             else 
                return 0.0;
        }  
      
        let res = 0.0;
        {
            let a = (t - this.knots[i]);
            let denom1 = (this.knots[i+k-1] - this.knots[i]);
            if(denom1 != 0)
              res += this.basis(k-1, i, t) * a/denom1;

            let b = (this.knots[i+k] - t);
            let denom2 = (this.knots[i+k] - this.knots[i+1]); 
            if(denom2 != 0)
              res += this.basis(k-1, i+1, t) * b/denom2;
        }
        return res;
    },
    
    t_min(){ return this.knots[this.order-1] },
    t_max(){ return this.knots[this.nbPoints()] },

    nbPoints(){ return this.ctrlPointInitList.length; },
    setNbpPoints(nb){  
        if( nb == this.nbPoints() )
            return;

        // generate new missing control points
        if(nb > this.nbPoints())
        {            
            for(let i = this.ctrlPointInitList.length; i < nb; ++i){
                this.ctrlPointInitList.push( 
                    new THREE.Vector3(i*2, i%2==0? 5.0 : -0.5, 0.0) 
                ); 
            }
        }
        
        this.ctrlPointInitList.length = nb;

        if( this.order > nb )
            this.order = nb;

        this.update();
    },

    set_custom_knots(knots){
        console.assert( knots.length == this.order + this.nbPoints() );
        this.knots = knots;
    },

    set_node_to_uniform()
    {
        const n = this.nbPoints() - 1;
        this.knots.length = this.order + n + 1;

        let step = 1.0 / (n - this.order+2);
        for (let i = 0; i < this.knots.length; ++i){
            this.knots[i] = i * step  - step * (this.order - 1);
        }
    },

    set_node_to_open_uniform()
    {
        this.knots.length = this.order + this.nbPoints();

        let acc = 1;
        for (let i = 0; i < this.knots.length; ++i)
        {
            if(i < this.order)
                this.knots[i] = 0.0;
            else if( i >= (this.nbPoints() + 1) )
                this.knots[i] = 1.0;
            else{
                this.knots[i] = acc / (this.nbPoints() + 1 - this.order);
                acc++;
            }
        }
        
        // This is a hack to make a pseudo open unifrom vector.
        // when doing so we allow that when t == t_max last 
        // point is properly extrapolated 
        this.knots[this.knots.length-1] += 0.01;
    },    

    update(){
        // todo move out to g_spline
        if( this.knot_type == "uniform") 
            this.set_node_to_uniform(); 
        else if( this.knot_type == "open_uniform") 
            this.set_node_to_open_uniform();
    }
};

g_bspline.update();


// ------------------------------------------------------------------------
// Three JS utils
// ------------------------------------------------------------------------

function createLine(color, nb_points, dim){
    let curveGeometry = new THREE.BufferGeometry();  
    const positions = new Float32Array( nb_points * dim ); // 3 vertices per point
    curveGeometry.setAttribute( 'position', new THREE.BufferAttribute( positions, dim ) );
    // Due to limitations of the OpenGL Core Profile with the WebGL renderer
    // on most platforms linewidth will always be 1 regardless of the set value. 
    const curveMaterial = new THREE.LineBasicMaterial({ color: color, linewidth: 2 });

    let curveLine = new THREE.Line(curveGeometry, curveMaterial);
    curveLine.position.set(0, 0, 0);
    curveLine.geometry.attributes.position.needsUpdate = true;
    return curveLine;
}

function updateCurve(curve, newPoints){
    for (let v = 0; v < newPoints.length; v++) {
        let p = newPoints[v];
        curve.geometry.attributes.position.setXYZ(v, p.x, p.y, p.z);
    }
    curve.geometry.attributes.position.needsUpdate = true;//
}

// -----------------------------------------------------------------------------

let g_bspline_mesh = 
{
    bspline: g_bspline, 
    resolution: g_bspline.resolution, 
    pointGeometry: new THREE.CircleGeometry(0.3 /*radius*/, 32),
    pointMaterial: new THREE.MeshBasicMaterial({ color: 0xaa0000 }),
    ctrlPointMeshes:[],
    ctrlPointLine:null,
    curveLine: null,    
  
    ctrlPoint(i) {
        return this.ctrlPointMeshes[i].position.clone();
    },

    removeCtrlPoint(scene, draggableList) {    
        // remove previous instances of the curve:
        for (const p of this.ctrlPointMeshes) 
        {                       
            // remove p from draggableList
            const index = draggableList.indexOf(p);
            if (index > -1) {
                draggableList.splice(index, 1);
            }

            // p.geometry.dispose();
            // p.material.dispose();               
            scene.remove(p); 
        }
        this.ctrlPointMeshes.length = 0;
 
        if(this.ctrlPointLine != null)
        {          
            this.ctrlPointLine.geometry.dispose();
            this.ctrlPointLine.material.dispose();
            scene.remove(this.ctrlPointLine);
        }

    },

    // Add control points to scene
    addCtrlPoints(scene, draggableList) { 

        this.removeCtrlPoint(scene, draggableList);
               
        for (let i = 0; i < (this.bspline.nbPoints()); ++i)
        {    
            const p = this.bspline.ctrlPointInitList[i];
            const point = new THREE.Mesh(this.pointGeometry, this.pointMaterial);
            this.ctrlPointMeshes.push(point);
          
            point.position.set(p.x, p.y, p.z);
            //point.rotation.x = -Math.PI * 0.5;           
            
            scene.add(point);
            draggableList.push(point);
        }
        
        
        this.ctrlPointLine = createLine(0xaa0000, this.bspline.nbPoints(), 3);
        scene.add(this.ctrlPointLine);
      
        // Generate knot vector
        this.bspline.update();       
    },
  

  
    // sample bspline position at t in [0.0, 1.0]
    eval(t) {
        
        let x = 0;
        let y = 0;
        let z = 0;
        //console.log("this.knots.length");
        //console.log(this.knots.length);
        //let acc = 0;
        for (let i = 0; i < (this.bspline.nbPoints()); ++i)
        {
             let w = this.bspline.basis(this.bspline.order, i, t);
             let p = this.ctrlPoint( i ).multiplyScalar( w );
             // console.log(w);    
              //acc += w;
              x += p.x;
              y += p.y;
              z += p.z;
        }
        //console.log(acc);
        return new THREE.Vector3(x, y, z);
    },

    sampleCurve(curvePoints, segments) {
        for (let t = 0; t < segments; t += 1) {            
            //let u = t * (1.0 / (segments-1));
            let u = t / (segments-1); //this properly range from [0.0, 1.0] but as a hack we actually want to range [0.0, 1.0[

            // Because the basis is ill defined at t = 1.0 for open uniform knots...
            // We could discard the last point and replace it with the last control point though.
            u = this.bspline.t_min()* (1-u) +  this.bspline.t_max() * u;          
            //console.log( u );            
            let p = this.eval( u );
            //console.log( p );            
            curvePoints.push( p );
        }
    },
     
    addCurve(scene){
        if(this.curveLine != null)
        {          
            this.curveLine.geometry.dispose();
            this.curveLine.material.dispose();
            scene.remove(this.curveLine);
        }

        this.curveLine = createLine(0x3273a8, this.resolution, 3);
        scene.add(this.curveLine);
    },
  
    updateSplineCurve(){
        const curvePoints = [];
        this.sampleCurve(curvePoints, this.resolution);   
        updateCurve(this.curveLine, curvePoints);

        const ctrlPoints = [];
        for (let i = 0; i < (this.bspline.nbPoints()); ++i){            
            ctrlPoints.push( this.ctrlPoint( i ) );
        }
        updateCurve(this.ctrlPointLine, ctrlPoints);
        

    },
    
    
    
};

// -----------------------------------------------------------------------------

let g_basis_mesh = {
    bspline: g_bspline,
    resolution: g_bspline.resolution, 
    curveBasis: [], 
    
    removeBasisCurve(scene) {    
        // remove previous instances of the curve:
        for (const p of this.curveBasis){  
            if(p != null)
            {          
                p.geometry.dispose();
                p.material.dispose();
                scene.remove(p);
            }
        }
        this.curveBasis.length = 0;

    },

    addBasisCurve(scene){  
        this.removeBasisCurve(scene);

        for(let i = 0; i < this.bspline.nbPoints(); ++i){
            // color HSL(i, 54%, 43%)
            let hue = 360 * i / this.bspline.nbPoints();            
            let color = new THREE.Color("hsl(" + hue + ", 54%, 43%)");

            let basisMesh = createLine(color, this.resolution, 3);
            this.curveBasis.push( basisMesh );
            scene.add(basisMesh);      
        }
    },

    updateBasisFunc(){
        for(let i = 0; i < this.bspline.nbPoints(); ++i){
            const funcPoints = [];
            this.sampleBasisFunction(funcPoints, this.resolution, i); //      
            updateCurve(this.curveBasis[i], funcPoints);
        }
    },

    sampleBasisFunction(curvePoints, segments, i) {
        console.log( "basis range:" + this.bspline.knots[0] + " " +  this.bspline.knots.at(-1));        
        let scale = 4.0;
        let range = this.bspline.knots.at(-1) - this.bspline.knots[0];
        for (let t = 0; t < segments; t += 1) {
            
            let u = t / (segments-1);
            u = this.bspline.knots[0] + range * u;
            //console.log( u );            
            let p = this.bspline.basis(this.bspline.order, i , u );
            curvePoints.push( new THREE.Vector3( u*scale, p*scale, 1)  );
        }
    },
}; 
// -----------------------------------------------------------------------------

function meshSetup(scene, draggableObjects) 
{
    // Add Bézier curve and control points:
    g_bspline_mesh.addCtrlPoints(scene, draggableObjects);    
    g_bspline_mesh.addCurve(scene);    
    g_basis_mesh.addBasisCurve(scene);
    g_bspline_mesh.updateSplineCurve();     
    g_basis_mesh.updateBasisFunc();        
    
}

// -----------------------------------------------------------------------------

function createDragControl()
{
    let dragControls = new DragControls(g_draggableObjects, g_camera, g_renderer.domElement);

    dragControls.addEventListener('dragstart', function () {
        g_controls.enabled = false;
    });
    dragControls.addEventListener('dragend', function () {
        g_controls.enabled = true;
    });
    return dragControls;
}

// -----------------------------------------------------------------------------
// Setup scene
// -----------------------------------------------------------------------------
function init() {
    let container = document.createElement('div');
    document.body.appendChild(container);

    g_camera = g_cam_params.createThreeJsCamera();
    g_camera.position.set(0, 0, g_cam_params.frustumSize); 
    g_camera.lookAt(0, 0, 0);

    g_scene = new THREE.Scene();
    g_scene.background = new THREE.Color(0xffffff); //0xa0a0a0

    if (true) {
        let light1 = new THREE.HemisphereLight(0xffffff, 0x444444);
        light1.position.set(0, 200, 0);
        g_scene.add(light1);

        let light2 = new THREE.DirectionalLight(0xbbbbbb);
        light2.position.set(0, 200, 100);
        light2.castShadow = true;
        light2.shadow.camera.top = 180;
        light2.shadow.camera.bottom =  - 100;
        light2.shadow.camera.left =  - 120;
        light2.shadow.camera.right = 120;
        g_scene.add(light2);
    }


    let w = g_cam_params.frustumSize*2.0;
    let grid = new THREE.GridHelper(
            w /*size*/,
            w /*divisions*/,
            0x000000, 0x999999);
    //grid.divisions = 2;
    grid.position.set(0,0,-1);
    grid.rotation.x = -Math.PI * 0.5;
    grid.material.opacity = 1.0;
    grid.material.transparent = true;
    g_scene.add(grid);

    var canvas = document.querySelector('#' + g_canvasName);
    g_renderer = new THREE.WebGLRenderer({
        antialias: true,
        canvas
    });
    g_renderer.setPixelRatio(window.devicePixelRatio);
    g_renderer.setSize(windowWidth(), windowHeight());
    g_renderer.shadowMap.enabled = true;
    document.body.style.margin = 0;
    document.body.style.padding = 0;
    document.body.style.overflow = 'hidden';
    document.body.style.position = 'fixed';
    
    window.addEventListener('resize', onWindowResize, false);

    g_controls = new OrbitControls(g_camera, g_renderer.domElement);
    g_controls.enableRotate = !g_cam_params.orthographic;
    g_controls.screenSpacePanning = true;
    g_controls.target.set(0, 0, 0);
    g_controls.update();

    

    meshSetup(g_scene, g_draggableObjects);   

    g_dragControls = createDragControl();    
}

// ---------------------------------------------------------------

function onWindowResize() {
    g_cam_params.update(g_camera);
    g_renderer.setSize(windowWidth(), windowHeight());

    // resize g_canvaContainer according to the size of g_canvasRootDiv:
    //let rect = g_canvasRootDiv.getBoundingClientRect();
    //g_canvaContainer.style.width = rect.width + "px";
       
    
}

// ------------------------------------------------------------------

function animate() {

    if(true){
        g_bspline_mesh.updateSplineCurve();
    }

    //g_bspline.curveLine.geometry.computeBoundingBox();
    //g_bspline.curveLine.geometry.computeBoundingSphere();
  
  
    requestAnimationFrame(animate);
    g_renderer.render(g_scene, g_camera);

}

// -------------------------------------------------------------------
// -----------------------------------------------------------------------------

init();
animate();

// -----------------------------------------------------------------------------
// -----------------------------------------------------------------------------

Python

Here is a static python version, that visualize the basis functions off static parameters inlined in the code:

"""
needed library:

In your command line do:
> pip install numpy
> pip install matplotlib 

to install the required dependencies of this code.

"""

import numpy as np
import matplotlib.pyplot as plt

# ------------------------------------------------------------------------------
# Global Parameters
# Appropriate knot vector will be generated based on these.
# ------------------------------------------------------------------------------

order = 3  # order of the B-spline
nb_points = 4  # Number of control points
knot_vector_type = "custom"  # "uniform" or "open_uniform" or "custom"

# if knot_vector_type == "custom", this will be used as the knot vector
# its size must be equal to (nb_points + order)
knots = [0.0, 0.0, 0.0, 1.0, 2.0, 2.0, 2.5]

# ------------------------------------------------------------------------------

"""
Computing B-spline basis function with the 
Cox-de Boor recursion
"""
# k: order
# i: ctrl point index / basis index.
def basis(k, i, t, knots):
    if k == 1:
        if knots[i] <= t < knots[i + 1]:
            return 1.0
        else:
            return 0.0

    res = 0.0

    numerator1 = t - knots[i]
    a = knots[i + k - 1]
    b = knots[i]
    denom1 = a - b
    if a != b:
        res += basis(k - 1, i, t, knots) * numerator1 / denom1

    numerator2 = knots[i + k] - t
    a = knots[i + k]
    b = knots[i + 1]
    denom2 = a - b
    if a != b:
        res += basis(k - 1, i + 1, t, knots) * numerator2 / denom2

    return res


"""
Same as the above (basis(k, i, t, knots)) 
except we print messages for debug
"""
# k: order
# i: ctrl point / basis index.
def basis_print(depth, k, i, t, knots):

    strin = ""
    for j in range(depth):
        strin += "    "

    if k == 1:
        print(strin + "t: " + str(t))
        print(strin + "knots[i]: " + str(knots[i]))
        print(strin + "knots[i + 1]: " + str(knots[i + 1]))
        if knots[i] <= t and t < knots[i + 1]:
            print(strin + f"yB(k: {k}, i: {i}) = 1.0")
            return 1.0
        else:
            print(strin + f"xB(k: {k}, i: {i}) = 0.0")
            return 0.0
        
    
    print(strin + f"B(k: {k}, i: {i})")

    res = 0.0

    numerator1 = t - knots[i]
    a = knots[i + k - 1]
    b = knots[i]
    denom1 = a - b
    if a != b:
        print(strin + "denom1" )
        res += basis_print(depth+1, k - 1, i, t, knots) * numerator1 / denom1

    numerator2 = knots[i + k] - t
    a = knots[i + k]
    b = knots[i + 1]
    denom2 = a - b
    if a != b:
        print( strin + "denom2" )
        res += basis_print(depth+1, k - 1, i + 1, t, knots) * numerator2 / denom2

    print(strin + f"B(k: {k}, i: {i}) = res {res}")
    return res
    


# @return size of the knot vector
def knot_size(order, nb_points):
    return nb_points + order



# knots : this knot vector.
# @return number of control points
def nb_ctrl_points(knots, order):
    return len(knots) - order
    

# builds a uniform knot vector 
# ex: [0 1 2 3 4 5 6]  (order = 3, nb_points = 4)
# @return list of floats representing the knot vector
def uniform_knots(order, nb_points) -> list[float]:
    assert( order <= nb_points)
    return [float(i) for i in range(knot_size(order, nb_points))]

# builds a open uniform knot vector
# ex: [0 0 0 1 2 3 4 5 6 7 8 9 10 10 10] (order = 3, nb_points = 15-3 = 12)
# @return list of floats representing the knot vector
def open_uniform_knots(order, nb_points):
    assert( order <= nb_points)
    a = [0.0 for i in range(order)] 
    b = [float(i+1) for i in range(knot_size(order, nb_points) - order*2)] 
    c = [float(knot_size(order, nb_points) - order*2 + 1) for i in range(order)]
    res = a + b + c    
    assert(len(res) == knot_size(order, nb_points))    
    return res


"""
Plot the B-spline basis functions for a given order and knot vector.
"""
def plot_bspline_basis_functions(order, knots):
    t = np.linspace(min(knots), max(knots), 1000)
    basis_functions = []

    for i in range(len(knots) - order):
        basis_function = [basis(order, i, x, knots) for x in t]
        basis_functions.append(basis_function)

    # check that the basis functions sum to 1 within t_min and t_max
    # print a message if not
    t_min = knots[order-1] 
    t_max = knots[-order]
    for t_i in t:
        sum = 0.0
        if t_i < t_min or t_i > t_max:
            continue
        for basis_function in basis_functions:
            sum += basis_function[np.where(t == t_i)[0][0]]
        if abs(sum - 1.0) > 0.0001:
            print(f"Warning: sum of basis functions at t = {t_i} is {sum}")

    
    plt.figure(figsize=(10, 6))
    for i, basis_function in enumerate(basis_functions):
        plt.plot(t, basis_function, label=f"Basis {i}")
    
    # add vertical lines for t_min = knots[order-1] and t_max = knots[-order]
    if False:
        plt.axvline(x=knots[order-1], color="black", linestyle="dashed")
        plt.axvline(x=knots[-order], color="black", linestyle="dashed")

    # add text labels for the x axis at t_min, t_max and knot vector indexes (u_i)
    if True:
        plt.text(t_min, -0.15, f"t_min", fontsize=10)
        plt.text(t_max, -0.15, f"t_max", fontsize=10)
        for i, knot in enumerate(knots):
            plt.text(float(knot), -0.18, f"u_{i}", fontsize=10)



    plt.title(f"B-spline Basis functions of order: {order} for {nb_ctrl_points(knots, order)} points. \n"+
              f"Curve defined for t in [{t_min}, {t_max}]"+
              f"\nKnot vector: {knots}")
    
    plt.xlabel("t")
    plt.ylabel("Basis Value")
    plt.legend()
    plt.grid(True)
    plt.show()




# ------------------------------------------------------------------------------


print ("order: " + str(order))
print ("degree: " + str(order-1))
print ("nb_points: " + str(nb_points))


if knot_vector_type == "uniform":
    knots = uniform_knots(order, nb_points)  
elif knot_vector_type == "open_uniform":
    knots = open_uniform_knots(order, nb_points)
elif knot_vector_type == "custom":
    assert( len(knots) == knot_size(order, nb_points) )
else:
    print("Error: unknown knot vector type")
    exit(1)


print("knot vector: ")
print( knots )

t_min = knots[order-1]
t_max = knots[-order]
print(" the curve is defined for t in [" + str(t_min) + ", " + str(t_max) + "]\n")


# Compute last basis function (index = nb_points-1) at t = t_max
r = basis_print(0, order, nb_points-1, t_max, knots)
print( f"Basis({nb_points-1}, {t_max}) debug: " + str( r ) ) 

r = basis(order, nb_points-1, t_max, knots)
print( f"Basis({nb_points-1}, {t_max}) main: " + str( r ) )

# Plot all basis functions
plot_bspline_basis_functions(order, knots)

Donate

No comments

Rodolphe Vaillant's homepage

Research, teaching and more...

Compute B-Spline Basis functions with Cox-de Boor recursion

Three JS app

Live application

Code Pen

Python