Introduction à l'optimization et problèmes de minimisation

FRENCH VERSION
Dumping my course notes from:
Cours "Méthode Numériques" Master 1 (2010) (Université Paul Sabatier)
Géneralité
Terminologie
Trouver $\mathbf X$ qui minimise la valeur $f(\mathbf X)$ avec $(\mathbf X = x_1, x_2, ..., x_n) \in \mathbb{R}^n$ et $f: \mathbb{R}^n \rightarrow \mathbb{R}$, sous les contraintes:- $C_i(\mathbf X) = 0, i \in [1, m']$
- $C_i(\mathbf X) \leq 0, i \in [m'+1, n]$
Le $\mathbf X$ pour lequel $f(\mathbf X)$ atteint son optimum minimum est noté $\mathbf X^*$ est appelé un minimiseur.
La valeur $f(\mathbf X^*)$ est applelé le minimum. Très souvent, on appelle ces deux objets minimum.
Notation courantes:
$$ \mathbf X^* = \underset{{\mathbf X \in \mathbb{R}^n}}{argmin} \left\{f(\mathbf X)\right\}\text{sans contraintes} $$ $$ \mathbf X^* = \underset{{\mathbf X \in (U \subset \mathbb{R}^n)}}{argmin} \left\{f(\mathbf X)\right\}\text{avec contraintes} $$ Suivant les domaines, $f$ est appelée: fonctionnelle, fonction de cout, fonction d'énergie, fonction objectif... Quelques domaines ou l'on utilise l'optimisation: physique, finance, recherche opérationnelle, image.Classes des problèmes d'optimisation
- Problèmes sans contraintes ou avec contraintes
- Problèmes linéaires ($f$ linéaire en $\mathbf X$ et $C_i$ linéaires en $\mathbf X$) ou non linéaires.
- Problèmes différentiables ($f$ differentiable) ou non différentiables ($C^1$ ou $C^2$)
- Problèmes en nombre réelles ($\mathbf X \in \mathbb{R}^n$) ou en nombres entiers ($\mathbf X \in \mathbb{Z}^n$)
Développement de Taylor
Formule générale:
$$f(x) =\sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k + R_n(x)$$Une unique variable réelle ($n=1$) dév limité en $x_0$ ordre 2:
$$ f(x) = f(x_0) + (x-x_0) f'(x_0) + \frac{ (x - x_0)^2 }{ 2 } f''(x_0) + \dots $$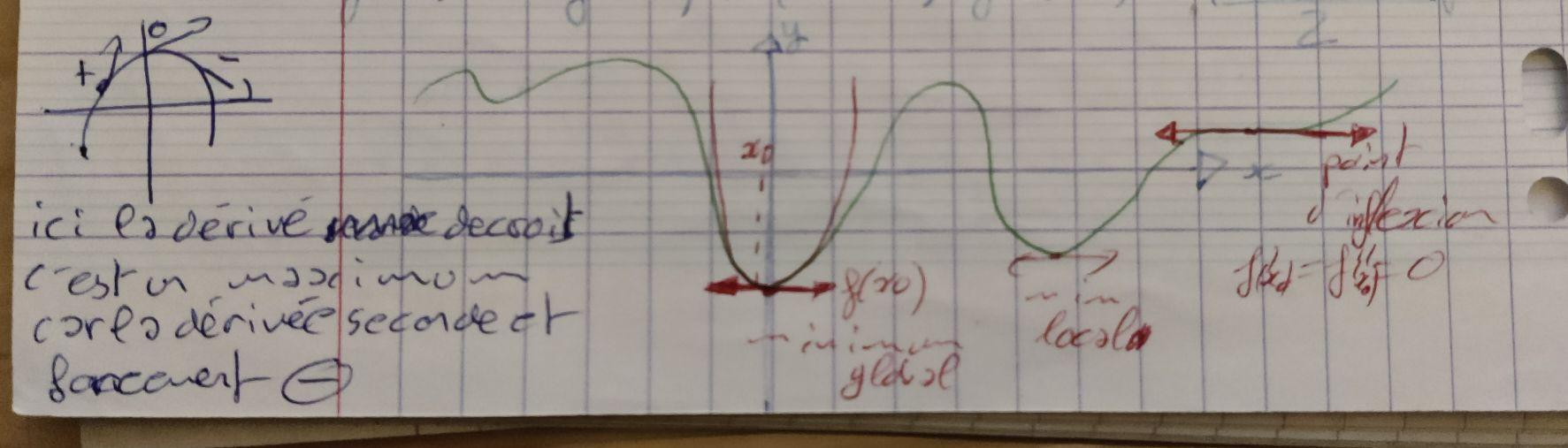
Une fonction dont la dérivé première est nulle en un point signifie qu'il y a un point d'inflexion (minium, maximum ou méplat). Si l'on regarde la dérivé seconde c'est maintenant la variation de la tangente en un point qui est mesurée.
Imaginons une parabole tourné vers le bas, la tangente ne cesse de diminuer passant de positif à négatif. C'est un maximum: la dérivé seconde et négative. Le raisonnement inverse peut être tenue pour une parabole tournée vers le haut.
Du point de vue du développement limité du second ordre en un point on approxime une fonction quelconque par une parabole, et le même raisonnement peut être tenue: Le signe de $f''(x_0)$ indique si la parabole est tournée vers le haut ($f''(x_0) > 0$) ou vers le bas ($f''(x_0) < 0$) ce qui nous indique si c'est un minimum ou maximum.
Pour une fonction $f: \mathbb R \rightarrow \mathbb R$, de classe $C^2$ un minimum (global ou local) est caractérisé par:
- $f'(x^*) = 0$
- $f''(x^*) > 0$
Cela caractérise aussi bien ce que l'on cherche (minimum global) que tous les minimums locaux.
Deux variables réelles ($n=2$) DL en $x_0$
Développement limité en nD, formule général pour l'ordre 2:
$$ t(\mathbf x) = f(\mathbf a) + \nabla f(\mathbf a)^T . (\mathbf x - \mathbf a) + \frac{1}{2} (\mathbf x - \mathbf a)^T . H[f(\mathbf a)] . (\mathbf x - \mathbf a) $$Développement de Taylor à l'ordre 2 en ($x_0, y_0$) (2D):
$$ \begin{array}{rcl} f(x,y) & = & \underbrace{f(x_0, y_0)}_\text{ordre 0} + \\ & & \underbrace{ \begin{aligned} (x-x_0)f_x(x_0, y_0) + \\ (y-y_0)f_y(x_0, y_0) + \\ \end{aligned} \\ }_\text{ordre 1} \\ & & \underbrace{ \begin{aligned} (x-x_0)^2 & f_{xx}(x_0, y_0) /2 + \\ (y-y_0)^2 & f_{yy}(x_0, y_0) /2 + \\ (x-x_0)(y-y_0) & f_{xy}(x_0, y_0) /2 + \\ (y-y_0)(x-x_0) & f_{yx}(x_0, y_0) /2 \end{aligned} }_\text{ordre 2} \end{array} $$Notation des dérivées partielles:
$$ f_x = \frac{\partial f}{\partial x}, f_y = \frac{\partial f}{\partial y} $$ $$ f_{xx} = \frac{\partial^2 f}{\partial^2 x}, f_{yy} = \frac{\partial^2 f}{\partial^2 y}, f_{xy} = \frac{\partial^2 f}{\partial xy}, f_{yx} = \frac{\partial^2 f}{\partial yx}$$Si $f$ est de classe $C^2$ alors $f_{xy} = f_{yx}$. Car le théoréme de Shwartz dit:
Soit $f: \mathbb R^n \rightarrow \mathbb R$ si $f$ est de classe $C^n$ alors le résultat d'une dérivation d'ordre $n$ ne dépend pas de l'ordre dans lequel les variables sont dérivées.
Nous allons réecrire le DL sous forme matricielle. Introduisons les notations necessaires.
Gradient de $f$ en $(x_0, y_0)$:
$$ G(x_0, y_0) = \begin{pmatrix} f_x(x_0, y_0)\\ f_y(x_0, y_0) \end{pmatrix} $$Hessienne de $f$ en $(x_0, y_0)$:
$$ H(x_0, y_0) = \begin{pmatrix} f_{xx}(x_0, y_0) & f_{xy}(x_0, y_0) \\ f_{yx}(x_0, y_0) & f_{yy}(x_0, y_0) \end{pmatrix} $$Chaque coefficients $H_{ij}(f)$ est définie comme:
$$ H_{ij}(f) = \frac{\partial^2f}{\partial x_i \partial x_j} $$Produit scalaire sous forme matricielle:
$$ V = \begin{pmatrix} a\\ b \end{pmatrix}, W = \begin{pmatrix} c\\ d \end{pmatrix} $$ $$ \mathbf V . \mathbf W = ac + bd \equiv \mathbf V^T \mathbf W = \begin{pmatrix} ac + bd \end{pmatrix} = \begin{pmatrix} ac + bd \end{pmatrix}^T = (\mathbf V^T \mathbf W)^T = \mathbf W^T \mathbf V $$On peut maintenant écrire le DL du second ordre de $f(x, y)$ sous forme matricielle:
$$f(x,y) = f(x_0, y_0) + (\mathbf X - \mathbf X_0)^T \mathbf G(x_0, y_0) + \frac{1}{2}(\mathbf X - \mathbf X_0)^T \mathbf H(x_0, y_0)(\mathbf X - \mathbf X_0) + \dots $$avec: $ \mathbf X - \mathbf X_0 = \begin{pmatrix} x - x_0\\ y - y_0 \end{pmatrix}$
Un minimum de f est caractérisé par:
- $\mathbf G(x^*, y^*) = (0, 0)^T$ (gradient nulle: en 2d veut dire qu'on est pile sur le sommet de la colline/plateau)
- $\mathbf H(x^*, y^*)$ Définie positive (i.e. $\mathbf V . \mathbf H . \mathbf V^T > 0$). Selon le 'signe' de $H$ on peut connaitre le sens de la concavitée car $H$ est liée à la notion de courbure de $f$. Par exemple le Laplacian d'une fonction 2D: $\Delta f = f_{xx} + f_{yy}$
$n$ variables réelles
DL à l'ordre 2 en $\mathbf X_0 \in \mathbb R^n$: $$f(\mathbf X) = f(\mathbf X_0) + (\mathbf X - \mathbf X_0)^T \mathbf G(\mathbf X_0) + \frac{1}{2} (\mathbf X - \mathbf X_0)^T \mathbf H(\mathbf X_0) (\mathbf X - \mathbf X_0) + \dots$$La Hessienne est une matrice carrée $n \times n$, pour laquelle on peut parler de diagonale. De plus, si $f$ est de classe $C^2$, c'est une matrice symétrique. (Théoréme de Schwartz)
Un minimum $\mathbf X^*$ de $f$ est caractérisé par:
- $G(\mathbf X^* ) = 0$, ou $\nabla f(\mathbf X^*)$ (equation d'Euler)
- $H(\mathbf X^* )$ définie positive
Ou $\mathbf X^*$ est le point du minimum.
Une matrix est définie positive ssi:
$\forall \mathbf X \in \mathbb R^n \backslash \{ 0 \}, \mathbf X^T \mathbf H(\mathbf X^*) \mathbf X > 0$(N.B: si non strictement positif ($\geq 0 $) on dit semi définie positive)
$$(\mathbf X - \mathbf X^*)^T \mathbf H(\mathbf X^*) (\mathbf X - \mathbf X^*) > 0 $$ Or: $$ \begin{eqnarray*} f(\mathbf X) & = & f(\mathbf X^*) + (\mathbf X - \mathbf X^*)^T \mathbf G(\mathbf X^*) + \frac{1}{2} (\mathbf X - \mathbf X^*)^T \mathbf H(\mathbf X^*) (\mathbf X - \mathbf X^*) + \dots \\ f(\mathbf X) - f(\mathbf X^*) & = & (\mathbf X - \mathbf X^*)^T \mathbf G(\mathbf X^*) + \frac{1}{2} (\mathbf X - \mathbf X^*)^T \mathbf H(\mathbf X^*) (\mathbf X - \mathbf X^*) + \dots \\ f(\mathbf X) - f(\mathbf X^*) - \dots & = & \frac{1}{2} (\mathbf X - \mathbf X^*)^T \mathbf H(\mathbf X^*) (\mathbf X - \mathbf X^*) \text{ , car } G(\mathbf X^*) = \mathbf 0 \end{eqnarray*} $$ D'où: $$f(\mathbf X) - f(\mathbf X^*) - \underbrace{ \dots }_\text{ce qui fait la diff entre min local et min global} > 0 $$Il se trouve que $\mathbf H(\mathbf X^*)$ est symétrique réelle, donc diagonalisable. Une matrice diagonalisable est définie positive si ses $n$ valeurs propres sont toutes positives.
N.B: pour les matrices non symétrique trouver si elle sont définie positives est plus compliqué que juste montrer que les vals propres sont positives (mais pas impossible)
Cas particulier des fonctionnelles $f$ quadratiques
$$f(\mathbf X) = f(\mathbf X^*) + (\mathbf X - \mathbf X^*)^T \nabla (\mathbf X^*) + \frac{1}{2} (\mathbf X - \mathbf X^*)^T \mathbf H(\mathbf X^*) (\mathbf X - \mathbf X^*)$$(Pas de points de suspension car on approxime un polygone du 2nd degrée avec un autre du 2nd)
D'où si il existe un minimum et que $f$ est quadratique alors ce minimum est unique et il s'agit du minimum global.
Mais il peut se produire qu'aucun minimum n'existe ! Par exemple pour $n=2$
$$ \begin{eqnarray*} z = f(x, y) & = & x * y \\ & = & \frac{x}{a}^2 - \frac{y}{b}^2 \text{, selle de cheval} \\ & = & x(x^2-3y^2) \text{, selle de singe} \end{eqnarray*} $$Exemples de fonctionnelles quadratiques
Étudions un problème concret d'optimisation issu des statistiques : estimation de la droite de régression de $Y$ en $X$
- données : $p$ points $(x_i, y_i)$ du plan, où tous les $x_i$ sont distincts.
- inconnues : paramètres $a$ et $b$ d'une droite d'équation $y = ax + b$, qui passe au plus près des points $(x_i, y_i)$

Si $p > 2$, il n'y a en général aucune solution exacte. On se contente de solutions approchées. Il y a plusieurs sens possibles pour ce concept de solutions approchées. Le plus simple est celui des solutions approchées aux sens des moindres carrées (fonctionnelle quadratique, on cherche le minimum d'une fonctionnelle)
Les équations à résoudre s'écrivent:
$$ \left \{ \begin{matrix} y_1 & = & a x_1 + b \\ \cdots \\ y_p & = & a x_p + b \\ \end{matrix} \right.\ $$On cherche a et b !
$$ \left \{ \begin{matrix} a x_1 + b & = & y_1 \\ \cdots \\ a x_p + b & = & y_p \end{matrix} \right.\ \Leftrightarrow \mathbf A \mathbf x = \mathbf b \Leftrightarrow \begin{bmatrix} x_1 & 1 \\ \vdots & \vdots \\ x_p & 1 \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} y_1 \\ \vdots \\ y_p \end{bmatrix} $$parce qu'il n'y a généralement pas de solutions exacte, on transforme ce problème en problème d'optimisation en introduisant la fonctionnelle :
$$f(a,b) = f(\mathbf x) = \sum_{i=1}^p (\underbrace{ \overbrace{(x_i a + b)}^y - y_i}_\text{(1)} )^2$$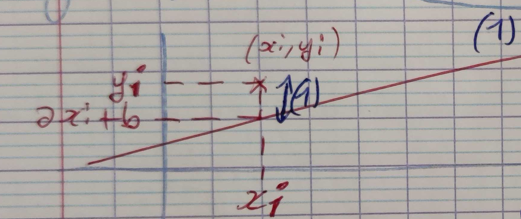
(1) Résidu associée à la ième équation, dont la valeur absolue est égale à la distance verticale du point $(x_i, y_i)$ à la droite d'équation $y = ax + b$
N.B: on peut voir $f$ comme une fonction d’énergie qui augmente quand la droite s'éloigne des échantillons.
Exprimons $f(\mathbf X)$ sous forme matricielle :
\begin{eqnarray*} f(\mathbf X) & = & \| \mathbf A \mathbf X - \mathbf B \|^2 \\ & = & \| \mathbf A (\mathbf X - \mathbf X_0 + \mathbf X_0) - \mathbf B \|^2 \\ & = & \| \mathbf A (\mathbf X - \mathbf X_0) + \mathbf A \mathbf X_0 - \mathbf B \|^2 \\ & = & \| \mathbf A \mathbf Y + \mathbf C \|^2 \text{, avec } \mathbf Y = \mathbf X - \mathbf X_0 \text{ et } \mathbf C = \mathbf A \mathbf X_0 - \mathbf B \\ & = & (\mathbf A \mathbf Y + \mathbf C)^T (\mathbf A \mathbf Y + \mathbf C) \\ & = & (\mathbf Y^T \mathbf A^T + \mathbf C^T) (\mathbf A \mathbf Y + \mathbf C) \\ & = & \mathbf Y^T \mathbf A^T \mathbf A \mathbf Y + \underbrace{\mathbf Y^T \mathbf A^T \mathbf C + \mathbf C^T \mathbf A \mathbf Y}_\text{2 termes transposés l'un de l'autre 1x1 donc égaux} + \mathbf C^T \mathbf C\\ & = & \mathbf Y^T \mathbf A^T \mathbf A \mathbf Y + 2 \mathbf Y^T \mathbf A^T \mathbf C + \mathbf C^T \mathbf C\\ & = & \color{red}\underbrace{(\mathbf X - \mathbf X_0)^T \mathbf A^T \mathbf A (\mathbf X - \mathbf X_0)} \color{black} + \color{green}\underbrace{2 (\mathbf X - \mathbf X_0)^T \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B)} \color{black} + \underbrace{(\mathbf A \mathbf X_0 - \mathbf B)^T (\mathbf A \mathbf X_0 - \mathbf B)} \\ & = & \color{red}\underbrace{(\mathbf X - \mathbf X_0)^T \mathbf A^T \mathbf A (\mathbf X - \mathbf X_0)} \color{black} + \color{green}\underbrace{2 (\mathbf X - \mathbf X_0)^T \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B)} \color{black} + \underbrace{ \| \mathbf A \mathbf X_0 - \mathbf B \|^2 } \end{eqnarray*}Or on sait que $f(\mathbf X)$ est égal à son DL d'ordre 2 :
$$f(\mathbf X) = \underbrace{ f(\mathbf X_0) } + \color{green} \underbrace{ (\mathbf X - \mathbf X_0)^T \nabla f(\mathbf X_0) } \color{black} + \color{red} \underbrace{ \frac{1}{2} (\mathbf X - \mathbf X_0)^T \mathbf H(\mathbf X_0) (\mathbf X - \mathbf X_0) } $$En identifiant les termes entre ces deux expressions, on obtient :
$$ \left \{ \begin{aligned} \nabla f(\mathbf X_0) &= 2 \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B) \text{, dépend de } \mathbf X_0 \\ \mathbf H( \mathbf X_0 ) &= 2 \mathbf A^T \mathbf A \text{, indépendant de } \mathbf X_0 \end{aligned} \right.\ $$Note: you will need to be familiar with the gradient rules to understand the following derivation.
Hessian of the Quadratic Function \( f(x) = \|Ax - b\|^2 \)
To find the Hessian of the quadratic function \( f(x) = \|Ax - b\|^2 \), we need to follow these steps:
-
Express the function in a more convenient form:
\[ f(x) = (Ax - b)^T (Ax - b) \] This can be expanded to: \[ f(x) = (Ax)^T (Ax) - 2b^T (Ax) + b^T b \] Simplifying, we get: \[ f(x) = x^T A^T A x - 2b^T A x + b^T b \]
-
Compute the gradient:
The gradient of \( f(x) \) with respect to \( x \) is given by: \[ \nabla f(x) = \frac{\partial f(x)}{\partial x} = 2A^T A x - 2A^T b \]
-
Compute the Hessian:
The Hessian matrix \( H \) is the second derivative of \( f(x) \) with respect to \( x \): \[ H = \nabla^2 f(x) \] Since the first derivative \( \nabla f(x) = 2A^T A x - 2A^T b \), taking the derivative with respect to \( x \) again, we get: \[ H = \nabla (\nabla f(x)) = 2A^T A \]
Thus, the Hessian of the function \( f(x) = \|Ax - b\|^2 \) is:
\[ H = 2A^T A \]
Equation d'Euler
Trouver le minimum de $f$ c'est trouver le point ou $\nabla f(\mathbf X_0) = 0$ (parfois appelé équations d'Euler). Dans notre cas $f$ est une quadratique et il n'y a qu'un seul minimum.
\begin{eqnarray*} \nabla f(\mathbf X_0) & = & 0 \\ 2 \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B) & = & 0 \\ \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B) & = & 0 \\ \mathbf A^T \mathbf A \mathbf X_0 - \mathbf A^T \mathbf B & = & 0 \\ \mathbf A^T \mathbf A \mathbf X_0 & = & \mathbf A^T \mathbf B \\ \end{eqnarray*}Pour rappel une matrix quelconque $M$ est symétrique si $M^T = M$. Ce qui signifie que $\mathbf A^T \mathbf A$ est symétrique car $(\mathbf A^T \mathbf A)^T = \mathbf A^T (\mathbf A^T)^T = \mathbf A^T \mathbf A$.
$$ A A^T = \begin{bmatrix} x_1 & \cdots & x_p \\ 1 & \cdots & 1 \\ \end{bmatrix} \begin{bmatrix} x_1 & 1 \\ \vdots & \vdots \\ x_p & 1 \\ \end{bmatrix} = \begin{bmatrix} {\color{blue} \sum_\limits{i=1}^p x_i^2} & \sum_\limits{i=1}^p x_i \\ \sum_\limits{i=1}^p x_i & {\color{purple} p} \\ \end{bmatrix} $$ $$ A^T B = \begin{bmatrix} x_1 & \cdots & x_p \\ 1 & \cdots & 1 \\ \end{bmatrix} \begin{bmatrix} y_1 \\ \vdots \\ y_p \\ \end{bmatrix} = \begin{bmatrix} \sum_\limits{i=1}^p x_i y_i \\ \sum_\limits{i=1}^p y_i \\ \end{bmatrix} $$Les équations d'Euler s'écrivent donc :
$$ \left (\sum_\limits{i=1}^p x_i^2 \right ) \ a + \left ( \sum_\limits{i=1}^p x_i \right ) \ b = \sum_\limits{i=1}^p x_i y_i \\ \left (\sum_\limits{i=1}^p x_i \right ) \ a + p \ b = \sum_\limits{i=1}^p y_i $$Lorsque la fonctionnelle f est quadratique, les equations d'euler sont linéaires et sont appellées équations normales. On est parti d'un systéme de $p$ équations linéaires en (a, b), sans solutions, on a maintenant un 2nd système de deux équations linénaires en $(a, b)$ :
$$ \underbrace{ \mathbf A \mathbf X = \mathbf B }_{\text{problème linéaire sans solution}} \Leftrightarrow \underbrace{ \mathbf A^T \mathbf A \mathbf X = \mathbf A^T \mathbf B }_{\text{problème linéaire avec solution au sens des moindres carrées}} $$Un systéme d'équations linéaires possédant le meme nombre d'équations que d'inconnues à généralement une solution unique. Il suffit pour cela que la matrice du système soit inversible (système de Cramer) :
$$ \begin{aligned} \mathbf A^T \mathbf A \text{ inversible } & \Leftrightarrow det(\mathbf A^T \mathbf A) \neq 0 \\ & \Leftrightarrow {\color{purple} p} {\color{blue} \sum_\limits{i=1}^p x_i^2} - \left ( \sum_\limits{i=1}^p x_i \right )^2 \neq 0 \\ \end{aligned} $$On peut montrer par récurence que:
$$det(\mathbf A^T \mathbf A) = \sum_{1 \leq i < j \leq p} (x_i - x_j)^2 \text{, (every pairs of }i, j\text{)}$$Cette expression ne s'annule que si $x_1 = x_2 = \dots = x_p$ or par hypothése toutes les abscices sont distinctes si $p \geq 2$ alors $det(\mathbf A^T \mathbf A) \neq 0$, donc il y a une solution unique :
$$ \mathbf X^* = (\mathbf A^T \mathbf A)^{-1} \mathbf A^T \mathbf B $$Il reste à montrer que $\mathbf X^*$ est bien un minimum de $f$ (ni un maximum, ni un point d'inflexion). Vérifions que $\mathbf H(\mathbf X^*)$ est définie positive :
\begin{eqnarray*} \mathbf X^T \mathbf H( \mathbf X^* ) \mathbf X & = & \mathbf X^T ( 2 \mathbf A^T \mathbf A ) \mathbf X \\ & = & 2 \mathbf X^T \mathbf A^T \mathbf A \mathbf X \\ & = & 2 (\mathbf X^T \mathbf A^T) \mathbf A \mathbf X \\ & = & 2 (\mathbf A \mathbf X)^T \mathbf A \mathbf X \\ & = & 2 \| \mathbf A \mathbf X \|^2 \geq 0 \text{ } (\forall \mathbf X \in \mathbb R^2) \\ \end{eqnarray*}$\mathbf H(\mathbf X^*)$ est au moins semi définie positive. Mais si $\mathbf X \neq 0$, est-ce qu'elle l'est strictement $\mathbf X^T \mathbf H( \mathbf X^* ) \mathbf X > 0$ ?
\begin{eqnarray*} \mathbf X^T \mathbf H( \mathbf X^* ) \mathbf X & = & 0 \\ \| \mathbf A \mathbf X \|^2 & = & 0 \\ \mathbf A \mathbf X & = & 0 \\ \underbrace{\mathbf A^T \mathbf A}_\text{inversible} \mathbf X & = & 0 . \mathbf A^T \\ \mathbf X & = & 0 \end{eqnarray*}N.B: $(A \Rightarrow B) \Leftrightarrow (\bar A \Rightarrow \bar B)$ donc $(\mathbf X^T \mathbf H( \mathbf X^* ) \mathbf X \neq 0) \Leftrightarrow \mathbf X \neq 0$
Conclusion
L'estimation des paramétres $a$ et $b$ de la droite de régression de $Y$ en $X$ (d'équation $y = ax + b$), au sens des moindres carrés, est un probléme d'optimisation (quadratique) qui admet une solution unique si $p \geq 2$ et si toutes les abscices sont distinctes. De plus on a l'expression exacte de la solution :
\begin{eqnarray*} \mathbf X^* & = & \underbrace{(\mathbf A^T \mathbf A)^{-1} \mathbf A^T }_\text{matrice pseudo inverse} B \\ \mathbf X^* & = & \mathbf A^+ + \mathbf B \end{eqnarray*}Interpretation de la pseudo inverse

$\mathbf A = \begin{bmatrix} x_1 & 1 \\ x_2 & 1 \end{bmatrix}$ est carrée et inversible ($\det(A) = x_1 - x_2 \neq 0$) donc on peut écrire $\mathbf A \mathbf X = \mathbf B \Leftrightarrow \mathbf X = \mathbf A^{-1} \mathbf B$. Maintenant, est-ce que cette solution exacte coincide avec la solution au moindre carrée ?
\begin{eqnarray*} \mathbf A^+ & = & (\mathbf A^T \mathbf A)^{-1} \mathbf A^T \\ & = & \mathbf A^{-1} (\mathbf A^T)^{-1} \mathbf A^T \text{ , car } \mathbf A \text{ est carrée} \\ & = & \mathbf A^{-1} \mathbf I \\ & = & \mathbf A^{-1} \\ \end{eqnarray*}d'où $\mathbf A^+ = \mathbf A^{-1}$ quand $\mathbf A$ est carrée.
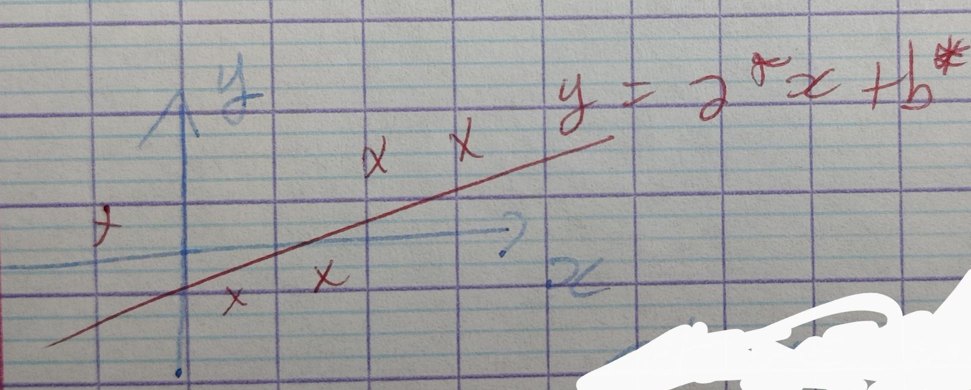
Pour ce probléme particulier on a $\mathbf X = \mathbf A^+ \mathbf B$ équivalent à $\mathbf X = \mathbf A^{-1} \mathbf B$
$$ \begin{bmatrix} a^* \\ b^* \\ \end{bmatrix} = \mathbf A^+ \mathbf B $$Est une solution exacte du 2éme problème (équation d'Euler) mais une solution approché du système initial : $f(\mathbf X^*) \gt 0$ (sauf cas très improbable)
Méthodes d'optimisation differentiable
Une seule variable $(n=1)$
On sait qu'un minimum (local ou global) est caractérisé par :
$$ \left \{ \begin{matrix} f'(x^*) = 0\\ f''(x^*) > 0 \end{matrix} \right.\ $$Ce n'est facile à résoudre que si :
- On connaît l'expression analytique de $f(x)$
- cette expression analytique n'est pas trop compliquée.
Dans le cas contraire on utilise des méthodes de résolutions numériques, qui ne fourniront qu'une valeur approchée du minimum. Si l'on connait $f(x)$ pour tout $x \in \mathbb R$ (ce qui n'est jamais le cas avec les images numériques) alors il existe deux types de méthodes de résolution.
Si l'on ne veut pas calculer de dérivées de $f$ on peut faire une recherche du minimum de $f$ par dichotomie (ou plus precisément par des méthodes inspiré de la dichotomie comme le golden section search. (bien sûr on n'a aucune garantie de trouver un minimum global) Pour une dichotomie pure on pourait l'appliquer à $f'$ pour trouver la racine $f'(x) = 0$.
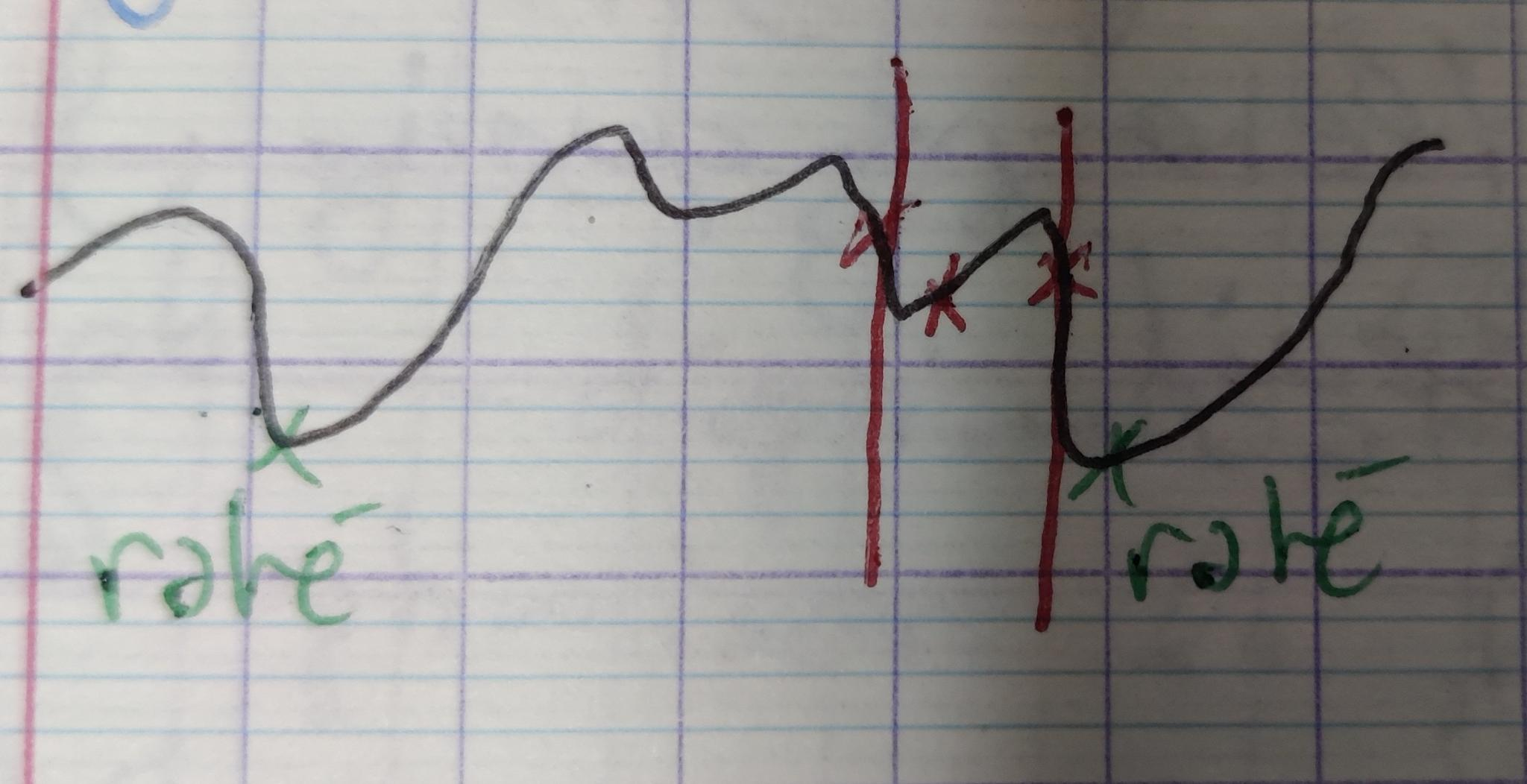
Alternativement on peut utiliser la méthode de Newton (Newton-Raphson étant la généralisation multi-dimensionel) pour trouver $f'(x) = 0$. Rappel de la méthode: on cherche $f(x) = 0$ en faisant l'approximation que $f$ est linéaire. On part d'une position $x^k$ arbitraire et on calcule un pas de déplacement $h$ censé satisfaire $f(x^k + h) = 0$.
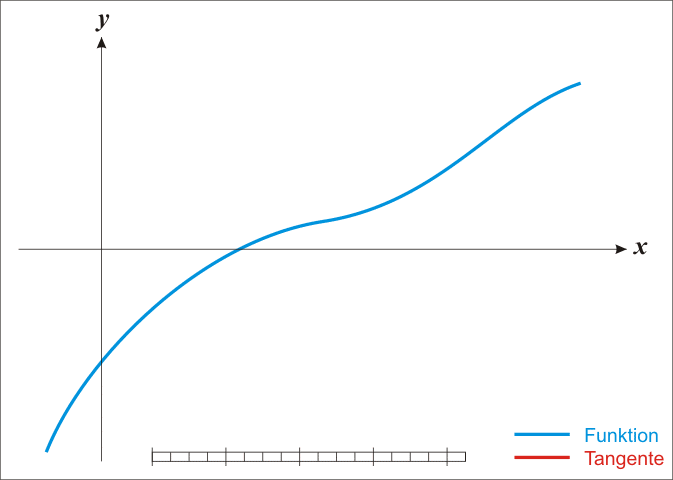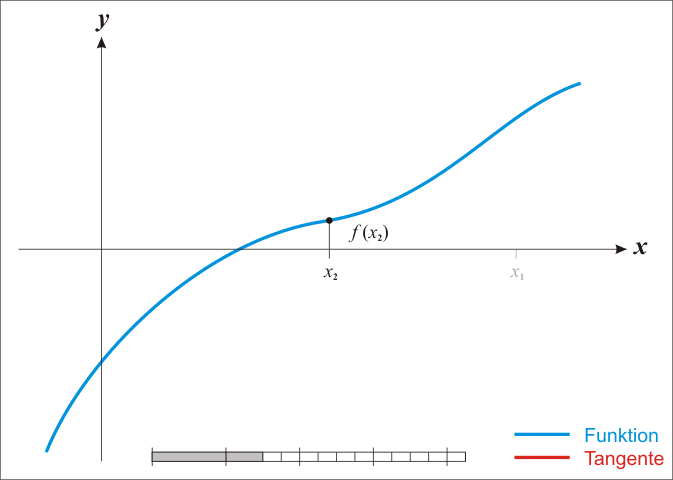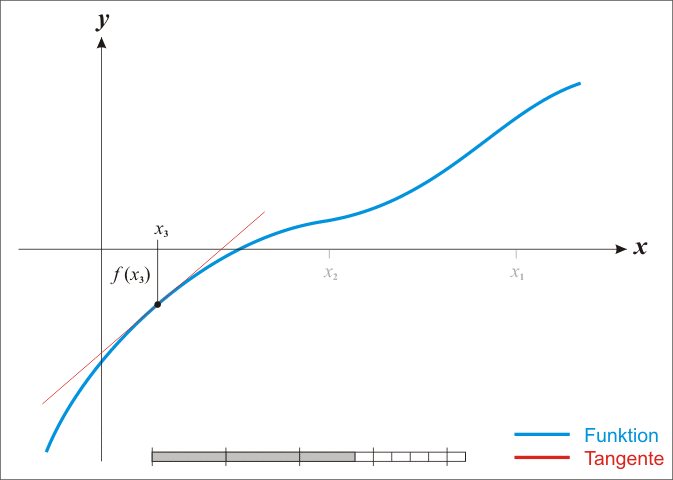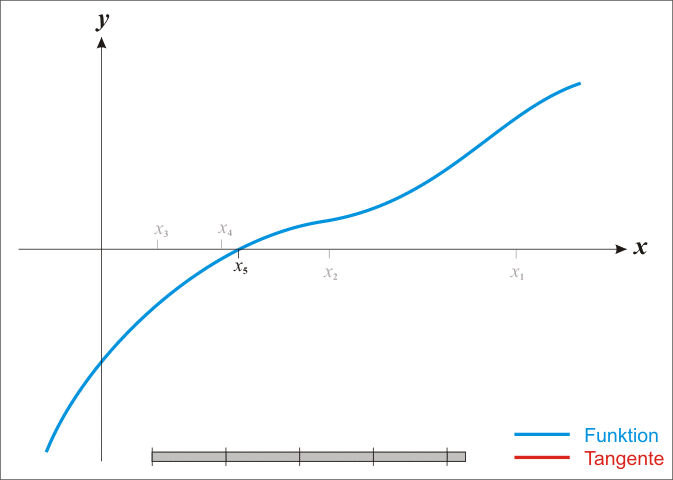
Si $f$ est effectivement linéaire il est facile de calculer $h$ avec une simple règle de trois. Pour tout $x$ on a $f' = \Delta y / \Delta x$. Autrement dit pour $\Delta y$ on avance de $\Delta x$. On veut savoir de combien se déplacer en $x$ sachant que $y = -f(x^k)$.
$$ \begin{array}{|c|c|c|} \hline \Delta y & -f(x^k) \\ \hline \Delta x & h \\ \hline \end{array} $$
Ce qui nous fait avec la règle de trois :
$$h = -f(x^k) \frac{\Delta x}{\Delta y} = -\frac{f(x^k)}{f'(x^k)}$$Mais en optimisation c'est $f'(x) = 0$ que l'on cherche. Rappelons le développement de Taylor Young:
$$ f(x) = \sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k + R_n(x)$$Maintenant reformulons avec $a=x$ et $X = x + h$ :
$$f(x+h) = \sum_{k=0}^n \frac{f^k(x) h^k}{k!} + R_n(x+h)$$On écrit ce DL pour $f'$ :
$$f'(x+h) = f'(x) + hf''(x) + \dots$$On cherche $h^*$ tel que :
$$ f'(x+h) = 0 \Leftrightarrow f'(x) + h^*f''(x) + \dots = 0$$et on se contente de :
$$h^* = -\frac{f'(x)}{f''(x)}$$La méthode de Newton consiste en l'itération suivante :
$$ x^{k+1} = x^k - \frac{f'(x)}{f''(x^k)} $$problèmes de cette méthode :
- On divise par $f''(x^k)$. Si ce nombre est nul ou très petit on peut être confronté à des instabilités numériques.
- Il n'y a pas de preuves de convergence locale ni même globale (contrairement à la dichotomie).
Comme critère d'arrêt, on peut utiliser :
- le critère de Cauchy ($x^{k+1}-x^k < \varepsilon$)
- nombre d'itérations $k = k_{max}$
- $|f'(x^k)| < seuil$
Cas multi-dimensionnel $(n>1)$
Pour $n>1$, il y a deux classes de méthodes :
- méthodes où on se ramène au cas unidimensionnel
- méthodes qui généralisent le cas unidimensionnel
Méthode de relaxation et méthode avec calcul du gradient
Pour tracer le graphe d'une fonction $f:\mathbb R^2 \Rightarrow \mathbb R$ (cas où $n=2$), on peut utiliser la représentation par courbes de niveau :
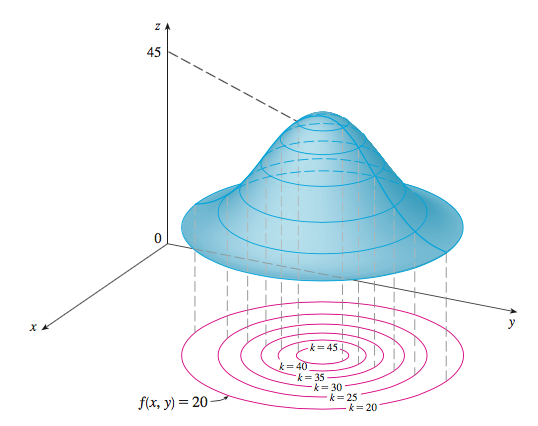
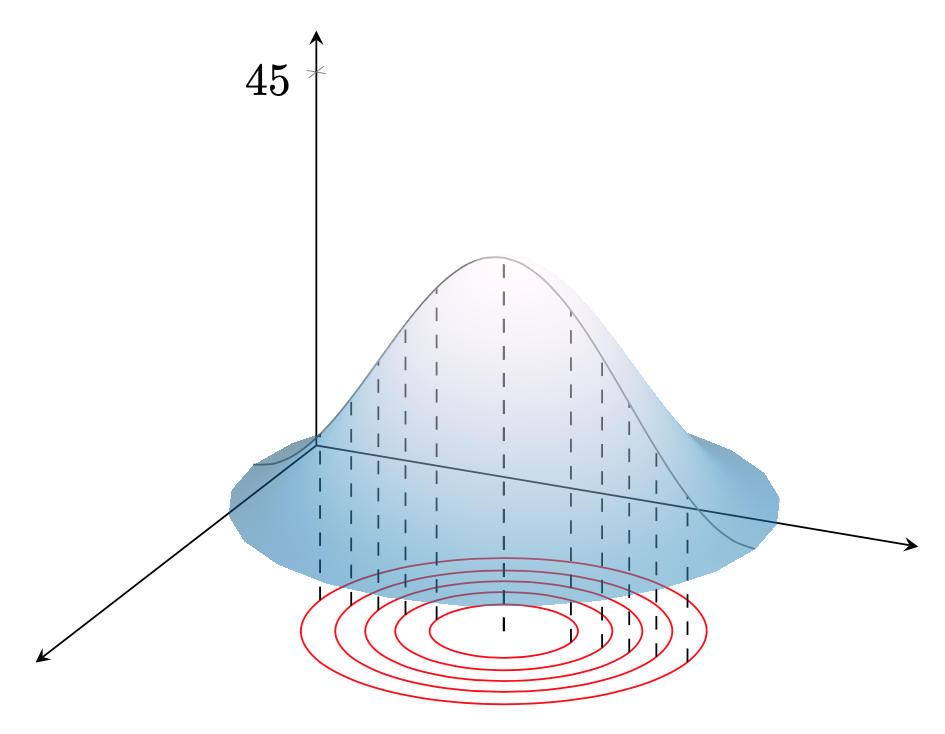
Toute coupe de cette surface par un plan vertical nous ramène au cas unidimensionnel.
Méthode de relaxation ("Line search")
On va se ramener au cas unidimensionnel en cherchant l'optimum uniquement sur une droite, pour n = 2, on ne se déplacera que sur l'axe x ou y. Partons d'une position initiale $(x_0, y_0)$ (estimation du minimum), on se déplace sur l'axe $x$ à la recherche d'un optimum de $f$ en fixant ($y = y_0$). Ce qui nous ramène donc à un problème d'optimisation unidimensionnel : on cherche à optimiser la fonction $f_1:\mathbb R \Rightarrow \mathbb R$, définie par $f_1(x) = f(x, y_0)$. Un optimum de $f_1$ se trouve en un point du plan où la droite $y = y_0$ est tangente à une courbe de niveau, en un tel point :
$$ \frac{ \partial f(x, y_0) }{ \partial x} = \frac{ d f_1(x) }{ d x} \text{ et } \frac{ \partial f(x_0, y) }{ \partial x} = \frac{ d f_2(y) }{ d y} $$Trouver un optimum de $f_1(x)$, c'est chercher les $x^*$ pour lesquels $\frac{ d f_1(x^*) }{ d x} = 0$, donc $ \frac{ \partial f(x^*, y_0) }{ \partial x} = 0$ c'est à dire $\nabla f(x^*, y_0)$ est vertical.
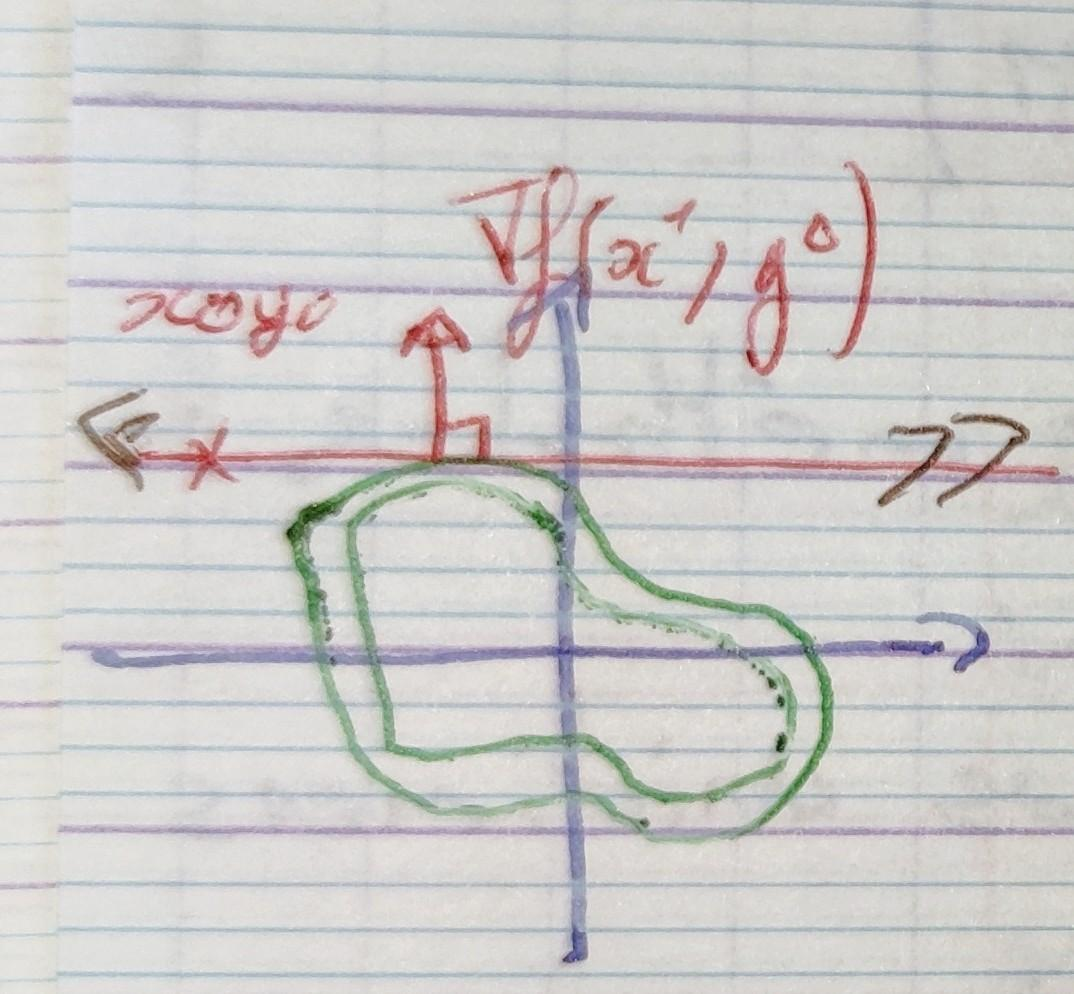
On choisit un de ces optimums $x^*$ et on itère avec $x^1 = x^*$. On va maintenant optimiser la fonction $f^2 : \mathbb R \Rightarrow \mathbb R$ définie par $f_2(y) = f(x^1, y)$.
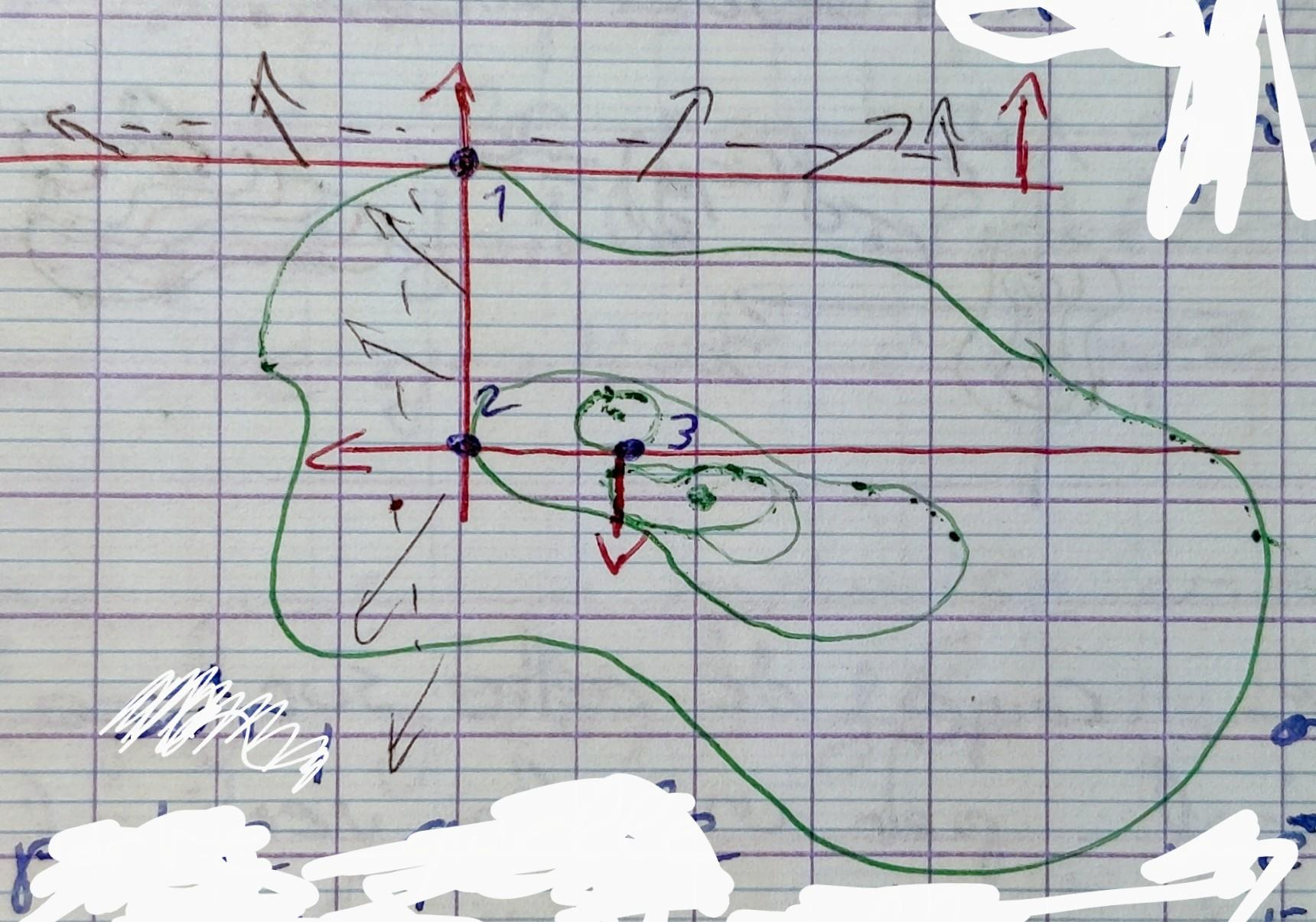
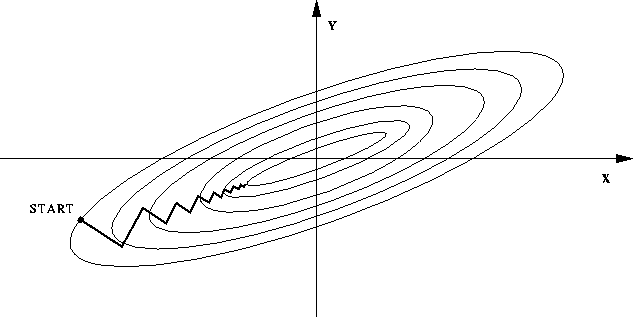
Bien sûr, on peut utiliser n'importe quelle méthode d'optimisation unidimensionnelle tel que Newton ou la Méthode du nombre d'or (golden ratio search). En plus des problèmes inhérent à la méthode de recherche unidimensionelle (e.g. instabilité numérique de la méthode de Newton si $f''$ est très petit) il y a un nouveau problème lorsqu'on traite une fonction nD. Il se peut qu'on mette beaucoup de temps à attendre un minimum local:

Même pour une fonction $f$ quadratique (ex: moindre carré) on risque de ne jamais atteindre exactement la solution et de faire des tout petits déplacements à chaque pas.
Méthodes avec calcul du gradient (steepest descent direction method)
Précedemment, les directions des axes étaient dépendantes du choix des variables, ce qui est relativement arbitraire. Il semblerait plus logique de se servir d'une direction invariante à un changement de variables, dans le cas de la méthode qui nous intéresse : la direction du gradient. L'approche est la même que pour la relaxation, mais on modifie $x$ et $y$ à chaque pas. En général le nombre de pas peut être beaucoup plus faible pour une convergence de précision égale. Cependand l'on doit calculer le gradient à chaque pas ce qui peut etre couteux en temps de calcul.
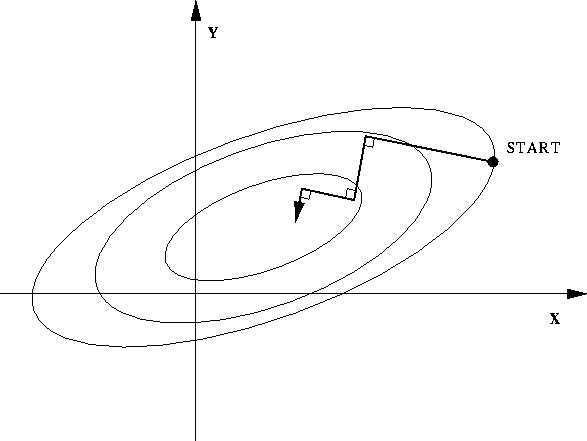
À chaque pas on optimise une fonction $g^i: \mathbb R \Rightarrow \mathbb R$ définie par $g^i(d) = f \Bigl ((x_i, y_i) + d \nabla f(x_i, y_i) \Bigr )$. On cherche l'optimum $d^*$ de $g_i$, puis on fait :
$$ (x^{i+1}, y^{i+1}) = (x^i, y^i) + d^*\nabla(x_i, y_i) $$On constate sur le dessin que les directions de recherche successives sont orthogonales entre elles. Il existe une variante de ces méthodes qui évite ce problème, appelée la méthode du gradient conjugué.
Généralisation de la méthode de Newton
La généralisation de la méthode de Newton au cas multidimensionnel de la méthode de Newton s'appelle la méthode de Newton-Raphson. Comme dans la méthode de Newton l'object et de marcher de façon itérative dans une direction $ \vec { \mathbf V} $ qui se rapproche du minimum qui se situe là ou le gradient et nul. Avant de le démontrer voici une itération de Newton-Raphson:
$$ \mathbf X^{k+1} = \mathbf X^k - \mathbf H(\mathbf X^k)^{-1} \ \nabla f (\mathbf X^k) $$Approximant notre fonction multidimensionel par son équivalent linéaire avec un DL de Taylor d'ordre 1 en $\mathbf a$ :
$$ f(\mathbf x) = f(\mathbf a) + \nabla f(\mathbf a)^T . (\mathbf x - \mathbf a) + \dots $$$a=\mathbf X$ and $x = \mathbf X + \Delta \mathbf X$
$$ f(\mathbf X + \Delta \mathbf X) = f(\mathbf X) + \nabla f( \mathbf X )^T \Delta \mathbf X + \dots $$si on remplace $f$ par $\frac{\partial f}{\partial x_i}$, $i = 1 \dots n$ alors :
$$ \frac{\partial f}{\partial x_i} (\mathbf X + \Delta \mathbf X) = \frac{\partial f}{\partial x_i} (\mathbf X) + \nabla \left(\frac{\partial f}{\partial x_i}\right)( \mathbf X )^T \Delta \mathbf X + \dots $$ $$ \left [ \nabla \left(\frac{\partial f}{\partial x_i}\right) \right ] = \left [ \frac{\partial^2 f(x)}{\partial x_1 x_i} \cdots \frac{\partial^2 f(x)}{\partial x_n x_i} \right ] \Leftrightarrow i \text{éme ligne de la Hessienne H(f(x))} $$D'où :
$$ \nabla f (\mathbf X + \Delta \mathbf X) = \nabla f(\mathbf X) + \mathbf H( \mathbf X) \Delta (\mathbf X) + \dots $$puisque l'on cherche $\nabla f(\mathbf X + \Delta \mathbf X) = 0$:
$$\mathbf H(\mathbf X) \Delta \mathbf X = - \nabla f(\mathbf X) - \cdots$$Donc le déplacement $\Delta \mathbf X$ vaut:
$$\Delta \mathbf X = \mathbf H^{-1} \nabla f(\mathbf X)$$Car la Hessienne est diagonalisable dans $\mathbb R$, et il suffit que toutes ses valeurs propres soient non nulles pour quelles soient inversibles.
Si $f$ était effectivement linéaire il suffirait d'effectuer un pas de l'itération ci-dessous pour en trouver le minimum:
$$ \mathbf X^{k+1} = \mathbf X^k - \mathbf H(\mathbf X^k)^{-1} \ \nabla f (\mathbf X^k) $$Les inconvénients sont les même que ceux de la méthode de Newton:
- Si une valeur propre de $H(X^k)$ est très petite alors il peut se produire des instabilités numériques
- Il n'y a pas de preuve de convergence
- A chaque étape il faut calculer le gradient et l'inverse de la Hessienne ou l'estimer de $f(\mathbf X^k)$. Dans la pratique on utilise souvent des variantes de cette méthode sans calculer l'inverse voir la Héssienne.
Cette méthode présente un gros avantage dans le cas d'une fonctionnel quadratique (moindre carré) puisque l'on à déjà calculé $\nabla f$ et $\mathbf H$ pour une fonction quadratique $f(X) = \| AX - B \|^2$:
$$ \left \{ \begin{matrix} \mathbf H( \mathbf X_0 ) = 2 \mathbf A^T \mathbf A \text{, indépendant de } \mathbf X_0 \\ \nabla f(\mathbf X_0) = 2 \mathbf A^T (\mathbf A \mathbf X_0 - \mathbf B) \text{, dépend de } \mathbf X_0 \end{matrix} \right.\ $$
$$ \begin{aligned} \mathbf X^1 &= \mathbf X^0 - \mathbf H(\mathbf X^0)^{-1} \ \nabla f(\mathbf X^0) \\ &= \mathbf X^0 - \frac{1}{2}(\mathbf A^t \mathbf A)^{-1} \ 2 \ \mathbf A^t ( \mathbf A \mathbf X^0 - \mathbf B) \\ &= (\mathbf A^t \mathbf A)^{-1} \mathbf A^t \mathbf B \\ \mathbf X^1 &= \mathbf A^{-1} \mathbf B \quad \text{ c'est l'optimum de f} \end{aligned} $$
Optimisation differentiable sous contraintes
Distance orthogonale à une droite
Avant de rentrer dans le vif du sujet nous avons besoin de définir la distance orthogonale d'un point $P = (x,y)$ à une droite de $\mathbb R^2$. Voyons comment retrouver cette distance, puis passons aux méthodes d'optimisations sous contraintes.
Nous allons utiliser l'equation cartésienne d'une droite (aussi appelé équation implicite) $D$: $ax + by = c$ avec $(a,b) \neq (0,0)$ et le vecteur $\vec v = \pm \begin{bmatrix} a \\ b \\ \end{bmatrix}$ est orthogonal à la droite $D$.
On veut calculer la distance de $P = (x,y)$ à son projeté orthogonal $\bar P(\bar x, \bar y)$ sur la droite $D$ que l'on notera $d_{\perp}(P,D)$
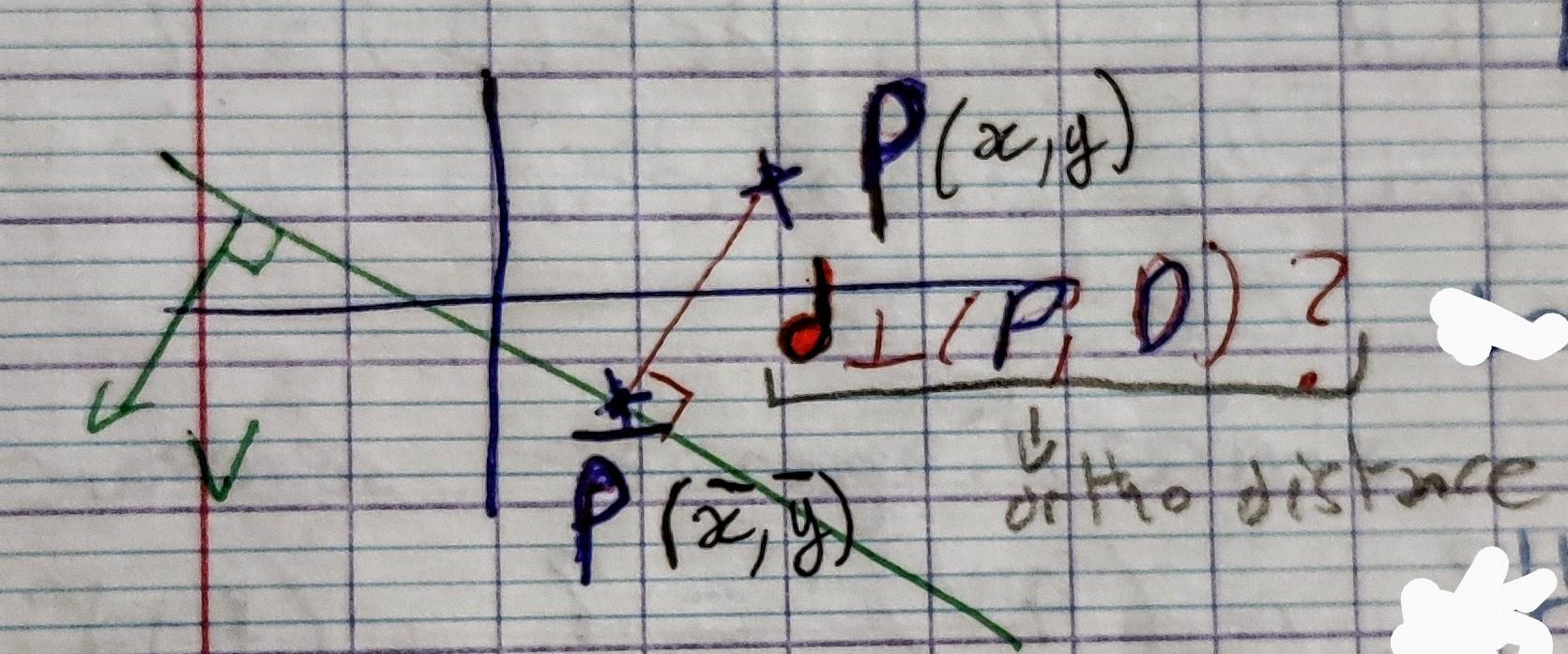
Raisonement géométrique
Prenons un cas simplifié, avec $c = 0$ et $\vec v$ un vecteur unitaire. Un point $P$ appartenant à la droite $D$ doit donc satisfaire $D(P(x,y)) = 0$ autrement dit $ax +by = 0$. On remarque qu'ici, l'équation de la droite est un simple produit scalaire $(P \cdot \vec v)$ facilement interpretable. c'est la distance du projeté du vecteur $\vec {OP}$ (ou $O$ est l'origine) sur $\vec v$. Tout point $P$ appartenant à la droite forme un vecteur $\vec OP$ orthogonale à $\vec v$ puisque le produit scalaire sera nulle à cette seul condition. Accesoirement $ax +by$ représente la distance orthogonale de $P(x,y)$ à la droite par définition du produit scalaire (et puisque $\vec v$ est unitaire). Une droite ne passant pas par l'origine sera représenté avec $c \neq 0$ par l'équation $ax +by = c$ le paramétre $c$ étant juste une valeur de compensation, le produit scalaire réstant la distance du projeté de $P$ sur $\vec v$, évaluer la distance orthogonale se fait simplement en évaluant la fonction de la droite: $D(P(x,y)) = ax + by -c$. Dans le cas ou $\vec v = \begin{bmatrix} a \\ b \\ \end{bmatrix}$ ne serait pas unitaire il faut toutefois normaliser la fonction implicite de la droite $D(P(x,y)) / \| \vec v \|$
$$ d_{\perp}(P(x,y), D(a,b,c)) = \frac{|ax+by-c|}{\sqrt{a^2 + b^2}} $$Raisonement numérique
Retrouvons la distance orthogonale à la droite par un raisonement plus numérique. On calcul le produit scalaire de $v$ par $\vec {\bar p \ p}$
$$ \begin{aligned} v^T \cdot \vec {\bar p \ p} &= \begin{bmatrix} a & b \end{bmatrix} \begin{bmatrix} x - \bar x \\ y - \bar y \end{bmatrix} \\ &= a (x - \bar x) + b (y - \bar y) \\ &= ax + by - (a \bar x + b \bar y) \\ v^T \cdot \vec {\bar p \ p} &= a x + by -c \text{ (puisque $\bar P \in D$ nous avons $a \bar x + b \bar y = c$) } \end{aligned} $$ $$ v^T \cdot \vec {\bar p \ p} = a x + by -c $$Résidu en $P$ de l'équation cartésienne de $D$
D'autre part:
$$ \begin{aligned} v^T \cdot \vec {\bar p \ p} &= \| v \| \ \| \vec {\bar p \ p} \| cos(\vec v, \vec {\bar p \ p}) \\ \| \vec {\bar p \ p} \| &= \frac{ v^T \cdot \vec {\bar p \ p} } { \| v \| } cos(\vec v, \vec {\bar p \ p}) \\ \end{aligned} $$avec
$$\left \{ \begin{aligned} \| v \| &= \sqrt{a^2 + b^2} &\\ \| \vec {\bar p \ p} \| &= d_{\perp}(P,D) & \text{ ce que l'on recherche} \\ cos(\vec v, \vec {\bar p \ p}) &= \pm 1 & \text{ car vecteurs paralléles} \\ \end{aligned} \right . $$D'où:
$$ \begin{aligned} \| \vec {\bar p \ p} \| &= d_{\perp}(P(x,y), D(a,b,c)) \\ &= \frac{ v^T \cdot \vec {\bar p \ p} } { \| v \| } \\ &= \frac{|ax+by-c|}{\sqrt{a^2 + b^2}} \end{aligned} $$Cas particulier: équation cartésienne normalisée, c'est à dire où $\|v\| = 1$ :
Posons $\begin{bmatrix} \bar a \\ \bar b \\ \bar c \\ \end{bmatrix} = \begin{bmatrix} a / \sqrt{a^2+b^2} \\ b / \sqrt{a^2+b^2} \\ c / \sqrt{a^2+b^2} \\ \end{bmatrix}$ ou l'on retrouve bien $ \sqrt{ \bar a^2 + \bar b^2 } = 1$
La version non normalisé: $ax + by = c$ $\overset{ (a,b) \neq (0,0) }{\Rightarrow}$ version normalisé: $\bar a x + \bar b y = \bar c$
On à donc:
$$ d_{\perp}(P,D) = | \bar a x + \bar b y - \bar c | $$Intersection de m droites de $\mathbb R^2$
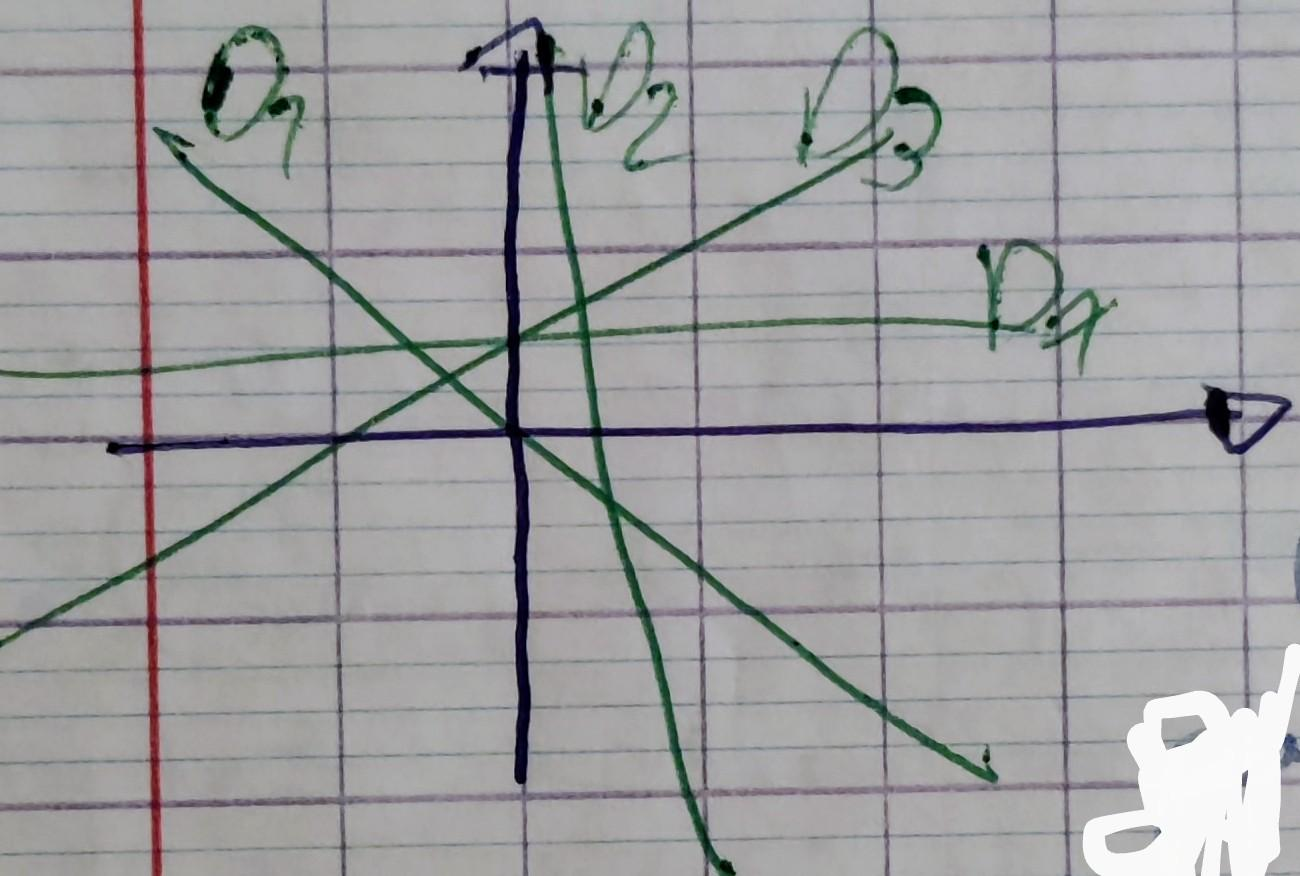
On cherche le point $P^*(x^*, y^*)$ qui soit le "plus près" des $m$ droites $D_1, \dots, D_m$. Par exemple, on cherche le point qui minimise la somme des carrés des $m$ distances orthogonales :
$$ f(x,y) = \sum_{i=1}^m d_{\perp}(P_i, D_i)^2 = \sum_{i=1}^m \left ( \frac{ (a_i x + b_i y - c_i) }{ \sqrt{a^2 + b^2} } \right )^2 = \sum_{i=1}^m \left ( { \bar a_i x + \bar b_i y - \bar c_i }\right )^2 $$C'est une fonctionnelle quadratique. Le système à résoudre au sens des moindres carrés est linéaire: $AX=B$ avec $X = \underset{2 \times 1}{ {\begin{bmatrix} x \\ y \end{bmatrix}} }$, $A = \begin{bmatrix} \bar a_1 & & \bar b_1 \\ \vdots & & \vdots \\ \bar a_m & & \bar b_m \end{bmatrix}$, $B= \begin{bmatrix} \bar c_1 \\ \vdots \\ \bar c_m \end{bmatrix}$
$$ f(x,y) = \| AX - B \|^2 $$ $$ A^T A X = A^T B $$Equation d'Euler => équations normales condition nécessaire mais non suffisante.
Les cas problèmatiques sont
Pour $m=1$ (une seule droite) $A^T A$ est toujours de taille $2\times2$ mais :
$$ \begin{aligned} A &= [\bar a_1 \bar b_1] \\ &\Rightarrow \\ A^T A &= \begin{bmatrix} \bar a_1 \\ \bar a_2 \\ \end{bmatrix} \begin{bmatrix} \bar a_1 & \bar a_2 \end{bmatrix} \\ &= \begin{bmatrix} \bar a_1^2 & \bar a_1 \bar b_1 \\ \bar a_1 \bar b_1 & \bar b_1^2 \\ \end{bmatrix} \\ \end{aligned} $$Se qui implique un déterminant nulle :
$$ det(A^T A) = \bar a_1^2 \bar b_1^2 - (\bar a_1 \bar b_1)^2 = 0 $$ et $A^T A$ est donc non invertible. La solution n'est pas unique.
Si $m > 1$ (strictemnet plus d'une droite) mais toutes les droites sont parallèles entre elles, $A^T A$ n'est pas non plus inversible.
On suppose dorénavant que m > 1 et que les droites ne sont pas parallèles entre elles. La solution est alors unique et vaut:
$$ X^* = A^+ B $$
La Hessienne vaut $H(X) = 2 A^T A$ et est définie positive: $X^*$ est le minimum global de $f$.
Exemple
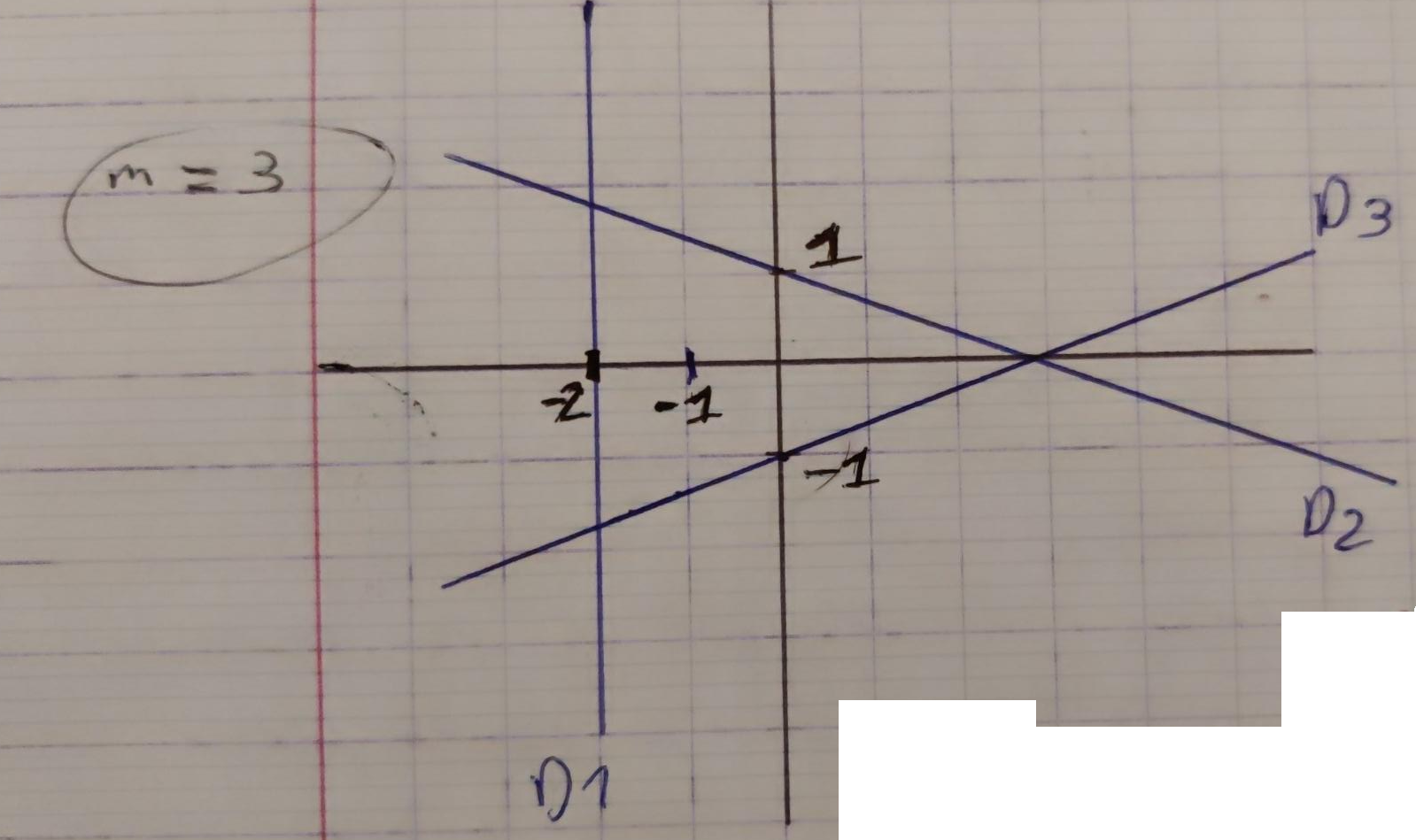
Comme ces 3 droites ne sont pas concurentes
![]() le minimum de $f(x,y)$ est $> 0$.
le minimum de $f(x,y)$ est $> 0$.
Equation d'Euler
$$ \nabla f(x,y) = 0 $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 2.(1).(x+2) + 2.(1).(x+y-1) / 2 + 2.(-1).(-x+y+1) / 2 &= 0 \\ 0/2 + 2.(1).(x+y-1)/2 + (1) .2.(-x+y+1)/2 &= 0 \\ \end{aligned} \right . $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 2(x+2) + (x+y-1) - (-x+y+1) &= 0 \\ (x+y-1) + (-x+y+1) &= 0 \\ \end{aligned} \right . \Leftrightarrow $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 2x + 4 + x + y - 1 + x -y -1 &= 0 \\ x + y -1 -x + y + 1 &= 0 \\ \end{aligned} \right . $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 4x + 2 &= 0 \\ 2 y &= 0 \\ \end{aligned} \right . $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} x &= -1/2 \\ y &= 0 \\ \end{aligned} \right . $$ $$ A = \begin{bmatrix} D_1: & 1 & 0 \\ D_2: & 1/\sqrt 2 & 1/\sqrt 2 \\ D_3: & -1/\sqrt 2 & 1/\sqrt 2 \\ \end{bmatrix} $$ $$ \begin{aligned} A^TA &= \begin{bmatrix} 1 & 1/\sqrt 2 & -1/\sqrt 2 \\ 0 & 1/\sqrt 2 & 1/\sqrt 2 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 1/\sqrt 2 & 1/\sqrt 2 \\ -1/\sqrt 2 & 1/\sqrt 2 \\ \end{bmatrix} \\ &= \begin{bmatrix} 2 & 0 \\ 0 & 1 \\ \end{bmatrix} \text{inversible donc une solution unique existe} \end{aligned} $$ $$ f(x^*, y^*) = f(-1/2, 0) = (3/2)^2 + 1/2 (3/2)^2 + 1/2(3/2)^2 = 9/2 $$Optimisation sous contraintes
Jusqu'à présent on a cherché le minimum de $f(x,u)$ dans $\mathbb R^2$. Il existe deux types de contraintes :
- Contraintes de type égalité : $c(x, y) = 0$ (equation implicite d'une courbe dans le plan)
- Contraintes de type inégalité : $c(x,y) \geqslant 0$ (partie du plan limité par la courbe d'équation implicite $c(x,y) = 0$
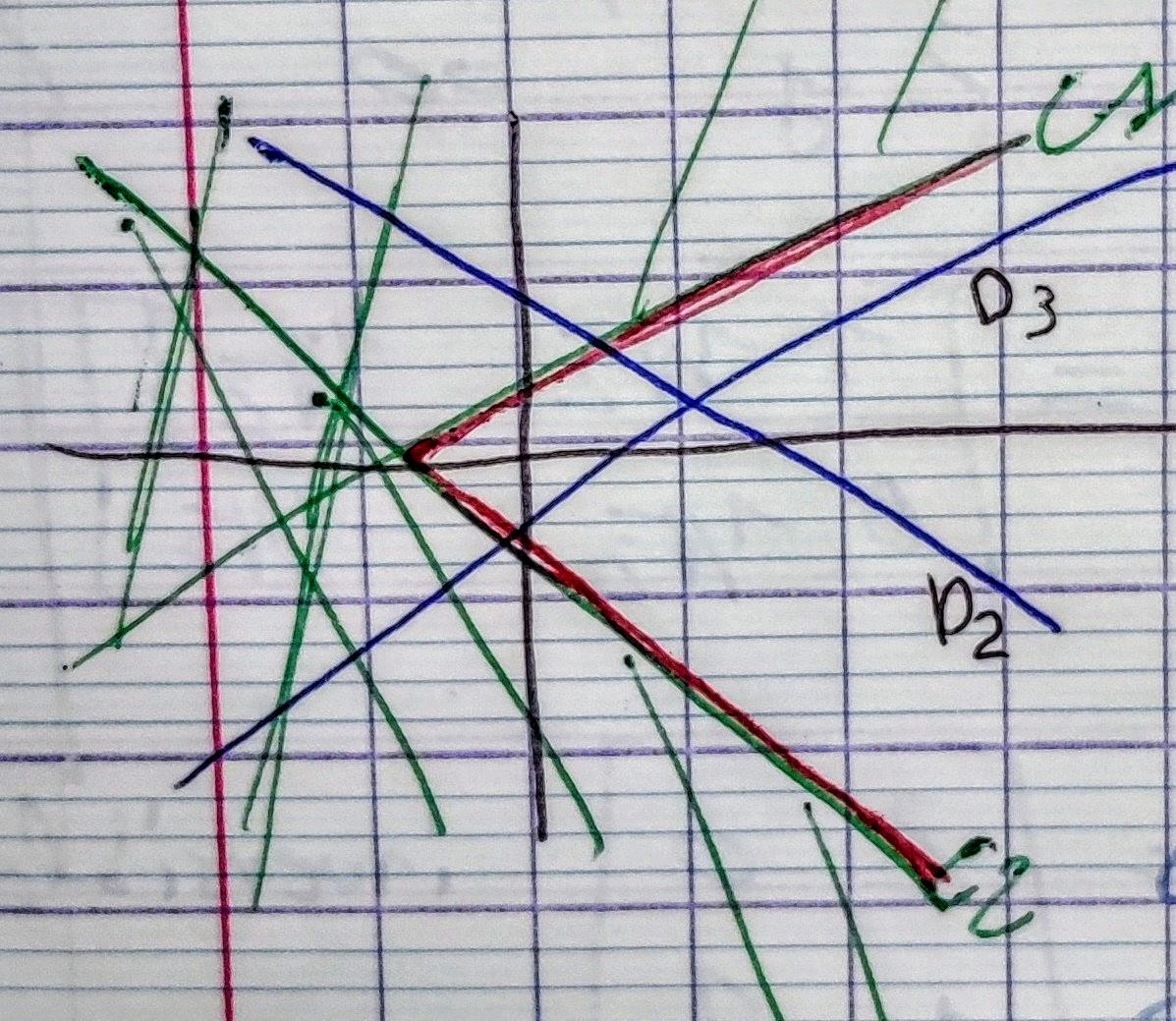
On va se restreindre à des contraintes linéaires, c'est à dire de droites dans $\mathbb R^2$
Contraintes de type égalité
Tracé des courbes de niveaux de $f(x,y)$
On revient sure l'exemple des droites non concurentes dont on cherche le point qui minimise les distances orthogonales. Les courbes de niveaux sont définies par :
$$ \begin{aligned} f(x,y) &= \frac{(x+2)^2}{1} + \frac{(x + y - 1)^2 }{2 } + \frac{(-x + y + 1)^2}{2 } \\ &= x^2 + 4x + 4 + (1/2) (y^2 + x^2 + 1 + 2xy - 2y - 2x + y^2 + x^2 + 1 - 2xy + 2y - 2x) \end{aligned} $$ $$ \begin{aligned} 2x^2 + y^2 + 2x + 5 &= K \text{ conique } \\ 2(x+1/2)^2 - 1/2 + y^2 + 5 &= K \\ (x+ 1/2)^2 + (y^2/2) = \frac{K - (9/2)}{2} \end{aligned} $$ellipses $C(-1/2, 0) = (x^*, y^*)$
N.B: équation canonique de l'ellipse:
$$ \frac{(x-x_c)^2}{a^2} + \frac{(y - y_c)^2}{b^2} = 1 $$Le paramétre $K$ est forcement $\geqslant 9/2$
Si l'on trace quelques éllipses de cette famille:
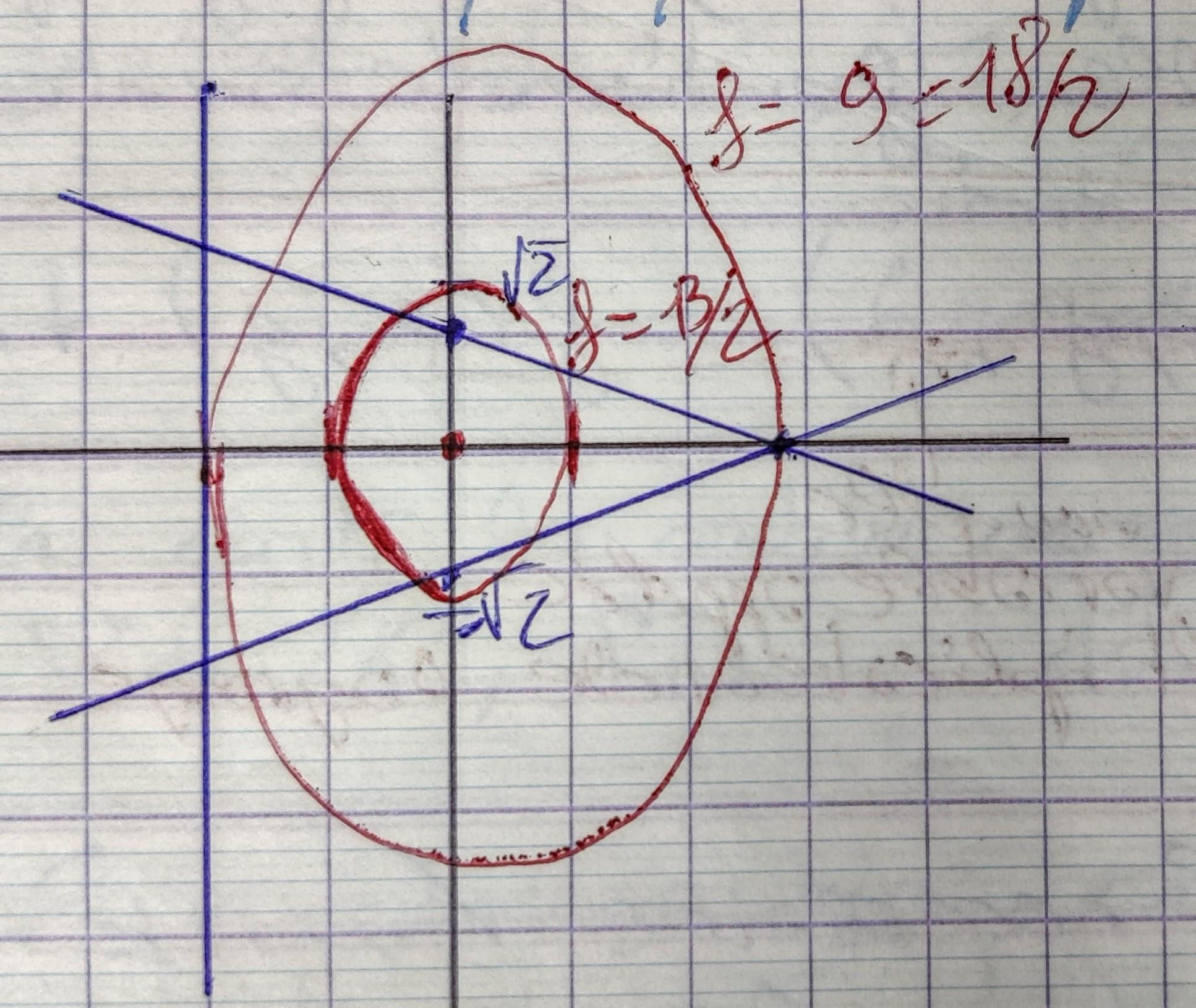
Multiplicateurs de Lagrange
Introduction visuelle
Ce qui suit n'est pas une preuve formelle mais une interprétation géométrique. Commençons avec l'exemple d'une droite (en noire) représentant notre contrainte $c(x,y)$, nous considérons seulement les valeurs de $f(x,y)$ qui passe par le plan de coupe en rouge:
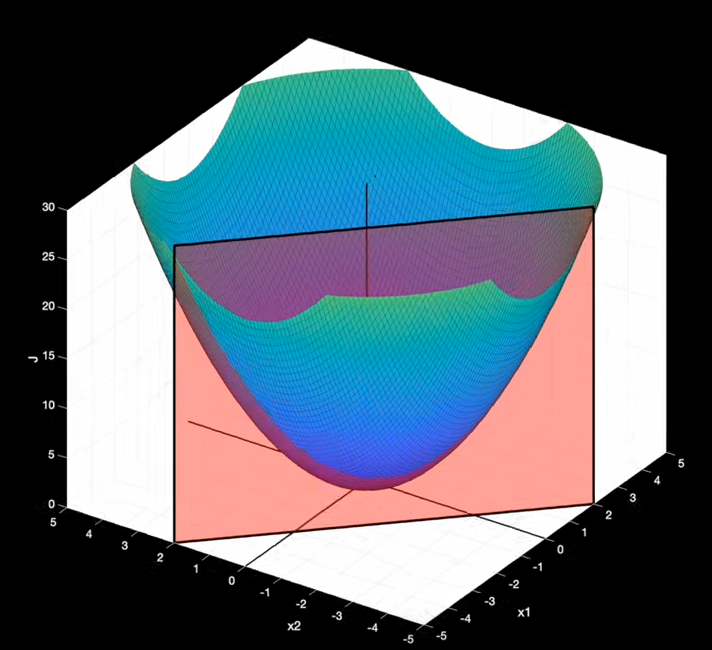
surface de $f(x,y)$ en bleu / vert, et la contrainte (plan de coupe rouge)
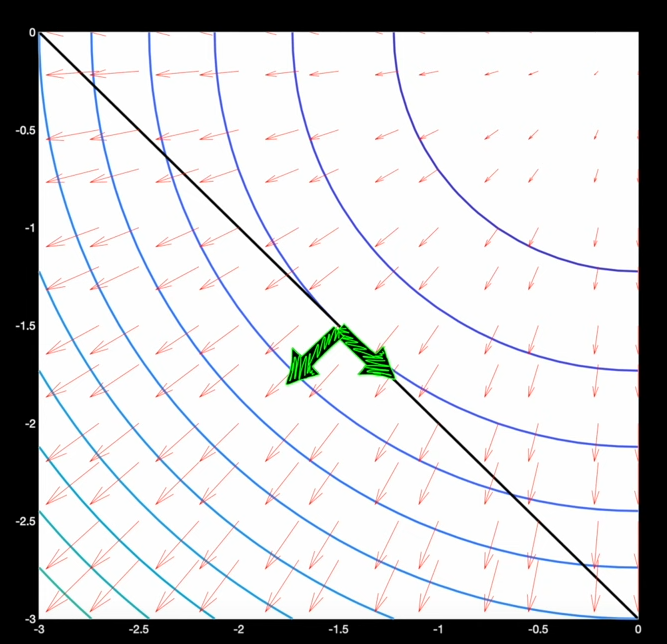
Lignes de niveaux de f(x,y) (lignes bleutés), et contrainte en noire
Lorsque l'on marche le long de la droite, sur notre chemin de randonné on traverse les lignes de niveaux de $f$, cela veut dire que le chemin est "pentue". Puisque lors de cette marche nous subissons des variations de pentes, il est alors logique d'observer que le gradient de $f$ est plus ou moins aligné à notre direction de marche (la droite noire). Dit de façon plus rigoureuse, $\nabla f$ est à minima non perpendiculaire à la droite $c(x, y) = 0$. Lorsque l'on arrive au minimum (ou maximum) de $f$ le chemin que nous emprentons devient "plat", il n'y a plus de variations de pente. Nous sommes dans le "creux" (ou le "sommet") c-a-d le minimum (ou maximum) de $f$. A ce moment là, le gradient $\nabla f$ est parfaitement perpendiculaire à notre chemin de marche (droite représentant la contrainte) puisque en ce point de $f$ il n'y a plus de variations de "pente". (vidéo)
On remarque facilement que le gradient $\nabla c$ à la courbe de niveau de la droite est lui aussi perpendiculaire (par définition du gradient, et ce, en tout point de la droite). D'où le fait que si $\nabla f$ et $\nabla c$ sont alignés, cela veut dire que l'on est sur un point de $f$ ou sur notre chemin de traverse le long de $c$ il n'y a pas de pente.
Contraintes 2D (i.e. inégalité $c(x, y) > k$): dans des dimensions plus élévées, le minimum ou maximum peut se trouver dans le sous-domaine de la fonction $f(x,y)$ délimité par la contrainte; ou bien, sur le bord de la contrainte.
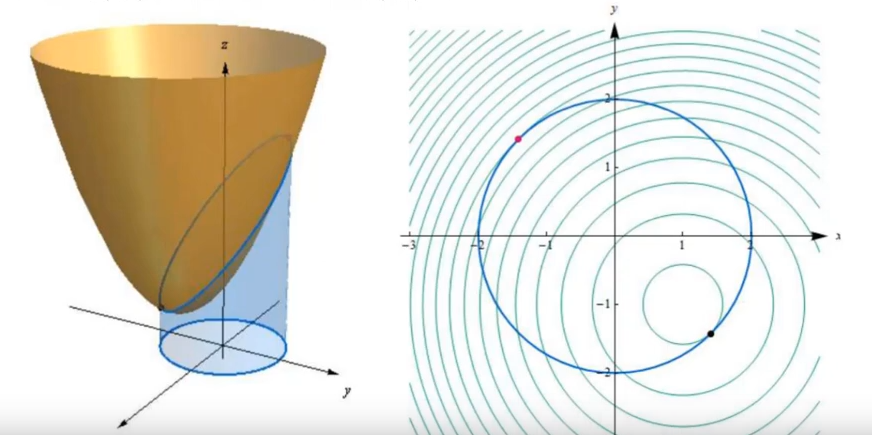
Comme mentionné plus haut, le min / max de $f$ se trouvant sur la contrainte apparait toujours lorsque les gradients de $f$ et de $c$ sont alignés, puisque en effet, marcher le long d'une courbe de niveau de $f$ signifie nécéssairement qu'il n'y a pas de variations de valeur de $f$. En d'autre termes, on cherche l'alignement ponctuel du chemin sur lesquel nous sommes contraint, et la courbe de niveau de $f$. Dire que le gradient de $f$ et $c$ sont alignés revient à dire que les tangentes au point (x, y) qui correspond aux courbes de niveaux de $f$ et $g = k$ sont alignés. C'est à dire, que notre marche le long de la contrainte est localement exactement aligné avec une ligne de niveau de $f$(vidéo):
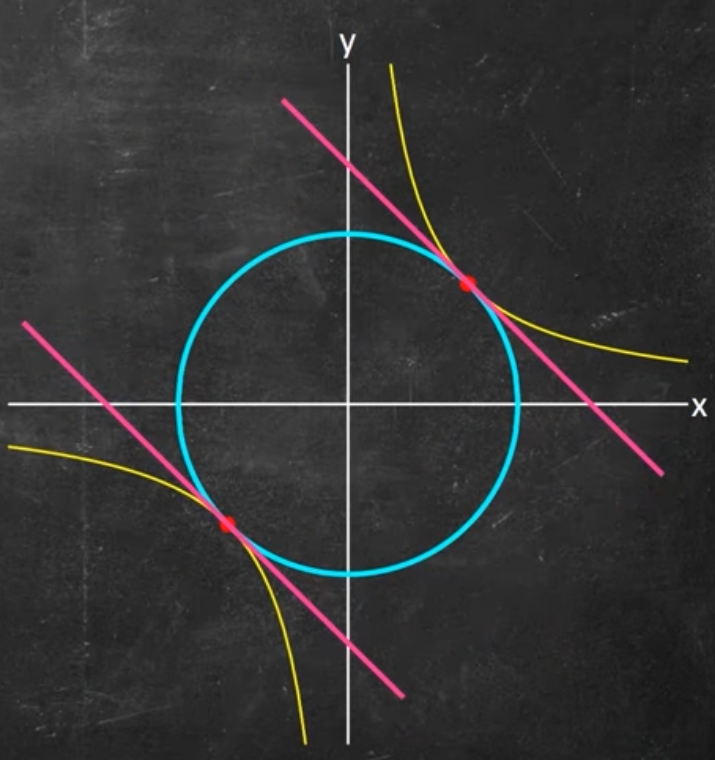
Une vidéo qui montre l'alignement des gradients:

Une autre explication visuelle que je trouve personnelement un peu moins clair
Video source: Understanding Lagrange Multipliers VisuallyEn violet le sous-domaine de $f$. La courbe rouge est le bord de la contrainte $c(x,y)$. Le cercle vert représente une unique iso-surface de la contrainte $c = k$.
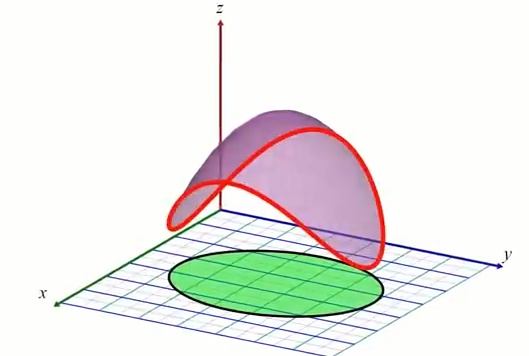
Pour un min ou max sur la contrainte, il se situeront nécessairement à un endroit de la courbe avec un mépla (en d'autre terme si l'on considérerait la courbe en 1D sa dérivée 1ére serait nulle):
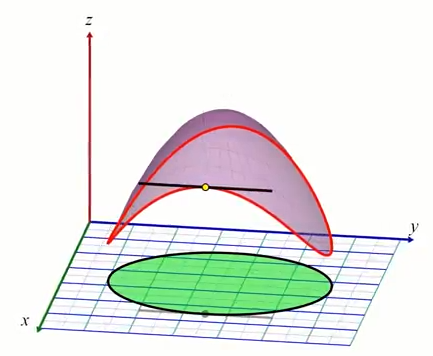
Il se trouve qu'un "méplat" de la courbe (rouge) de la contrainte est toujours tangent à la courbe de niveau de $f$ (violet). $f$ peut etre séctionné en une infinité de plans de coupes $xy$ générant une courbe de niveau, d'où le fait qu'une droite dans le plan $xy$ est nécessairement tangente à une courve de niveau de $f$. Sachant que par définition, le gradient est toujours perpendiculaire à une ligne de niveau, pour un point sur le min/max de la contrainte (méplat), le gradient $\nabla f$ est alors nécessairement perpendiculaire à cette tangente.
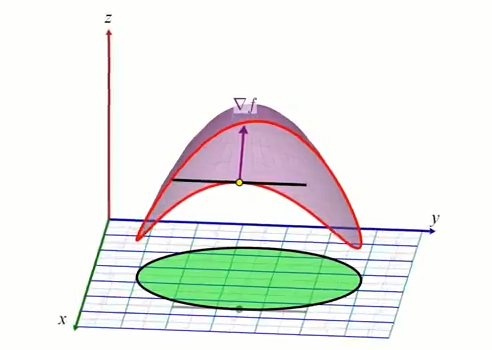
D'une façon similaire le gradient $\nabla c$ est aussi par définition perpendiculaire aux courbes de niveaux de $c$:
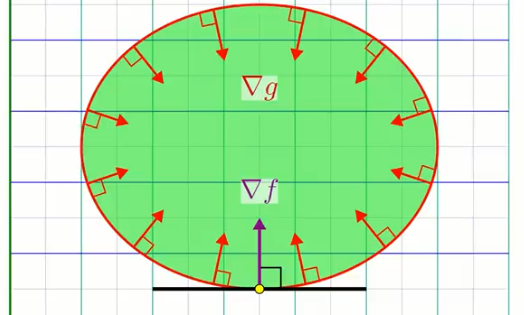
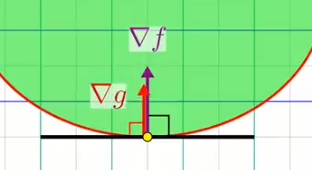
$\nabla c$ et $\nabla f$ sont donc paralléles dans le plan "xy". Un minimum ou maximum le long de la contrainte satisfait nécessairement: $\nabla f = \lambda \nabla c$
L'alignement des gradient se traduit par:
$$ \nabla f = \lambda \nabla c $$Ce qui est l'équivalent d'écrire ce qui suit (si l'on factorise the sign négatif dans $\lambda$:
$$ \nabla f + \lambda \nabla c = 0 $$La méthode pour trouver le maximum on minimum le long du bord de la contrainte consiste à résoudre le systéme d'équation suivant:
$$ \bbox[20px, border: 2px solid black]{\begin{aligned} \nabla f + \lambda \nabla c &= 0 \\ c(x,y) + k &= 0 \end{aligned}} $$où $\lambda$ est appelé le multiplicateur de Lagrange ("Lagrange multiplier"). Typiquement on résou pour $(x,y, \lambda)$ ou $\lambda$ est généralement ignoré. Les deux solutions trouvées représentent le minimum et maximum sur le bord de la contrainte.
Exemple
Prenons l'exemple d'une parabole $f(x_1, x_2) = x_1^2 + x_2^2$ et d'une droite $c(x_1, x_2) = x_1 + x_2 + 3 = 0$
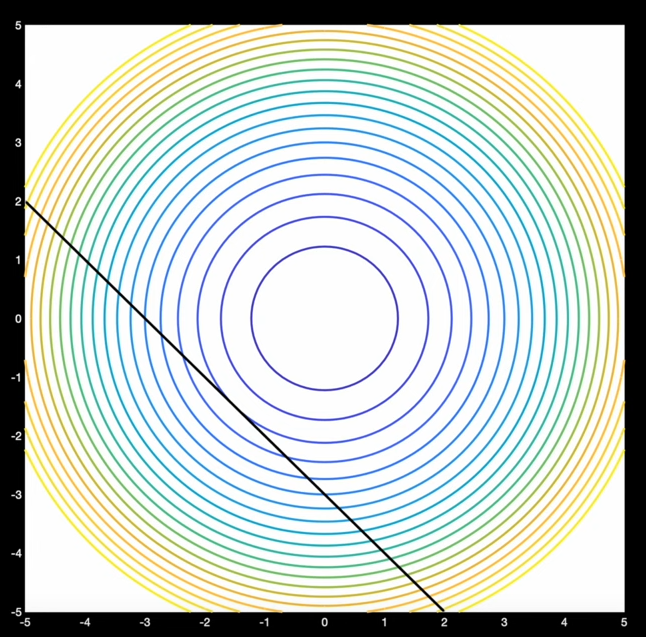
So we solve:
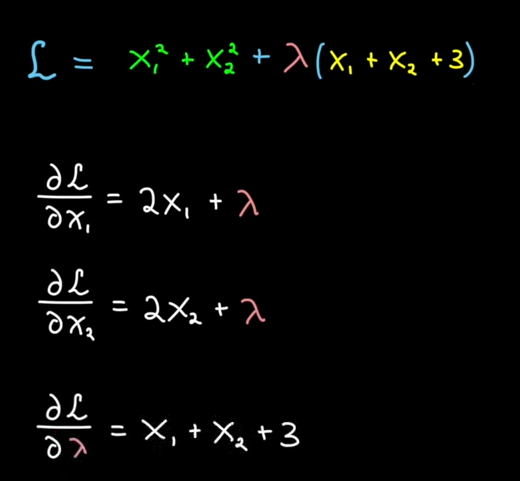
Solutions: $x_1 = -1.5$, $x_2 = -1.5$, $\lambda = 3$
Formellement
Lagrange est un Mathématicien Italien (18éme / 19éme). Si l'on cherche le minimum de $f(x,y)$ non plus dans $\mathbb R^2$ mais sur la droite d'équation $c(x,y) = 0$, alors une condition nécessaire est que:
$$ \nabla f \underbrace{(x^*, y^*)}_{ {\text{point vérifiant la contrainte } c(x,y)=0 \text{ qui minimise } f(x,y)}} \text{soit paralléle à } \nabla c(x^*, y^*) $$
Ceci est vrai pour une contrainte quelconque differentiable (pas forcement linéaire). On peut réécrire cette condition nécessaire (mais non suffisante)
$$ \begin{aligned} \exists \lambda \in \mathbb R \\ \nabla f(x^*, y^*) + \lambda \nabla c(x^*, y^*) &= 0\\ \Leftrightarrow \\ \nabla (f+ \lambda c)(x^*, y^*) &= 0\\ \end{aligned} $$Par ailleurs:
$$ c(x^*, y^*) = 0 $$L'idée (géniale) de Lagrange est d'introduire la nouvelle fonctionnelle suivante:
$$ \bbox[20px, border: 2px solid black]{ \mathcal{L}(x, y, \lambda) = f(x, y) + \lambda c(x, y) } $$Une nouvelle variable $\lambda$ appelé multiplicateur de Lagrange est introduite. La condition nécessaire (mais non suffisante) qui remplace les équations d'Eulers est:
$$ \bbox[20px, border: 2px solid black]{ \nabla \mathcal L (x^*, y^*, \lambda^*) = 0 } $$Attention: ici $\nabla$ dérive par rapport à $x$, $y$ et $\lambda$
Preuve
$$ \left \{ \begin{aligned} \left . \begin{aligned} \frac{\partial \mathcal L}{\partial x}(x^*, y^*, \lambda^*) = 0 \\ \frac{\partial \mathcal L}{\partial y}(x^*, y^*, \lambda^*) = 0 \\ \end{aligned} \right \} & \Leftrightarrow \nabla_{(x,y)} \left[ f(x^*, y^*) + \lambda^*c(x^*, y^*)\right] = 0 \\ \frac{\partial \mathcal L}{ \partial \lambda }(x^*, y^*, \lambda^*) = 0 & \Leftrightarrow c(x^*, y^*) = 0\\ \end{aligned} \right . $$On retrouve les deux égalités que doit vérifier la solution $(x^*, y^*)$, en prenant la valeur $\lambda = \lambda^*$
Bilan
Pour résoudre un problème d'optimization differentiable sous contraintes de type égalité $c_1(x) = 0, \cdots, c_m(x) = 0$ on procéde de la façon suivante en calculant:
$$ \bbox[20px, border: 2px solid black]{\mathcal L( x, \lambda_1, \cdots, \lambda_m) = f(x) + \sum_{i=1}^m \lambda_i c_i(x)} $$Note: autant de multiplieur $\lambda_m$ que de contraintes.
- on écrit la condition nécessaire:
$ \nabla \mathcal L( x, \lambda_1, \cdots, \lambda_m) = 0 $- On commence toujours par éliminer les multiplicateurs $\lambda_m$
Retour sur l'exemple
Contrainte linéaire:
$y=1 \Leftrightarrow c(x,y)=0$
$\mathcal L( x, \lambda) = 2x^2 + y^2 + 2x + 5 + \lambda (y-1)$
On résoud donc:
$\nabla \mathcal L (x, y, \lambda) = 0$
$\Leftrightarrow$
$ \left\{\begin{aligned} 4x + 2 &= 0 \\ 2y + \lambda &= 0 \\ y-1 &= 0 \end{aligned}\right. \Rightarrow $ $ \left\{\begin{aligned} x &= -1/2 \\ y &= 1 \\ \end{aligned}\right. $
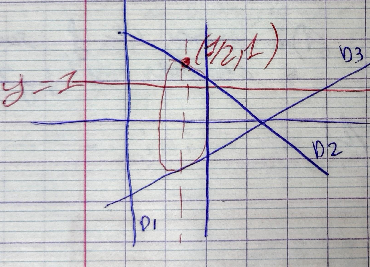
Contraintes non linéaires: $x^2 + y^2 = 1$
$$ \mathcal L(x, y, \lambda) = 2x^2 + y^2 + 2x + 5 + \lambda(x^2 + y^2 -1) $$ $$ \mathcal L_2(x,y, \lambda) = 0 $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} \text{(1) } \quad & 4x + 2 + 2 \lambda x &= 0 \\ \text{(2) } \quad & 2y + 2 \lambda y &= 0 \\ \text{(3) } \quad & x^2 + y^2 - 1 &= 0 \\ \end{aligned} \right . $$Ce système n'est pas linéaire car la contrainte n'est pas linéaire. Onélimine $\lambda$
$ y * \text{(1)} - x * \text{(2)} = 0-0 $
$ (4x + 2 + 2 \lambda x).y - (2y + 2 \lambda y).x = 0 $
$ 4xy + 2y + 2 \lambda xy - (2xy + 2\lambda xy) = 0 $
$ 4xy + 2y + 2 \lambda xy - 2xy - 2\lambda xy = 0 $
$ 2xy + 2y = 0 $
$ 2y( x + 1) = 0 $
Soit $y=0$ ou $x=-1$
En rajoutant la contrainte (3), on trouve 2 solutions: $(\pm 1, 0)$.
Nous n'avons pas la garantie que ces solutions soient des minimus de $f(x,y)$
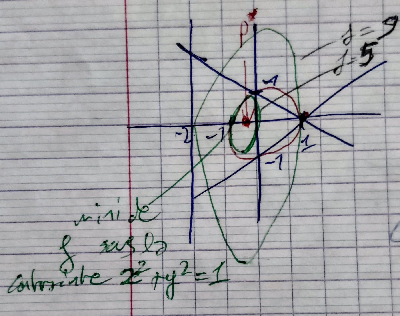
- $f( 1,0) = 9$ -> max de $f$ sous la contrainte.
- $f(-1,0) = 5$ -> min de $f$ sous la contrainte.
Contrainte de type inégalité
On écrit les contraintes sous la forme $c \geqslant 0$
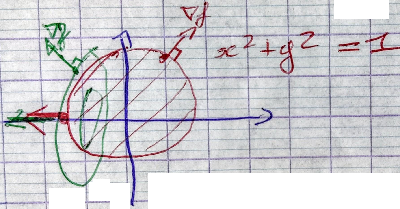
Si on l'impose $x^2 + y^2 - 1 \geqslant 0$, on introduit le meme Lagrangien que précedement:
$$ \mathcal{L}_2(x, y, \lambda) = f(x, y) + \lambda (x^2 + y^2 - 1) $$Il peut y avoir deux types de solutions:
$$ \exists \lambda < 0 \text{, } \nabla \bigl [ f + \lambda c \bigr ] (x^*, y^*, {\lambda}^*) =0 $$ $$ \Leftrightarrow $$ $$ \nabla f (x^*, y^*) = \underbrace{-{\lambda}^*}_{ > 0 } \quad \nabla c(x^*, y^*) $$Les deux gradients en $(x^*, y^*)$ sont paralléles et de meme sens. De plus, $c(x^*, y^*) = 0$. On dit que la contrainte $c(x,y) = 0$ est active.
$c(x^*, y^*) > 0$ on dit que la contrainte est inactive. Dans ce cas là on doit avoir $\nabla f(x^*, y^*) =0$ C'est similaire à de l'optimization sans contraintes.
Dans la pratique:
- On cherche les solutions du problème sans contraintes.
- on regarde si les solutions vérifient les contraintes.
- Si ce n'est pas, on calcule le Lagragien et on résout en $(X, \lambda_1, \cdots, \lambda_m)$ ce qui revient à rendre les contraintes actives.
Exemple:
$$ x^2 + y^2 \geqslant 1 \Leftrightarrow c(x,y) = x^2 + y^2 - 1 $$ $$ \nabla f(x, y) = 0 \Leftrightarrow \left \{ \begin{aligned} x &= -1/2 \\ y &= 0 \\ \end{aligned} \right . $$or:
$$ c(x^*, y^*) = (-1/2)^2 + 0^2 - 1 = -3/4 < 0 $$Le point $(x^*, y^*)$ ne vérifie pas la contrainte. On remplace la contrainte $c(x, y) = 0$ active.
$$ \mathcal L(x,y,\lambda) = f(x,y) + \lambda (x^2 + y^2 -1) $$ $$ \mathcal L(x,y,\lambda) = 0 $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 4x + 2 + 2 \lambda = 0 \\ 2y + 2 \lambda y = 0 \\ x^2 + y^2 - 1 = 0 \end{aligned} \right . $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} x = 1, y = 0, \lambda = 3 \\ \text{ou} \\ x=-1, y=0, \lambda=-1\\ \end{aligned} \right . $$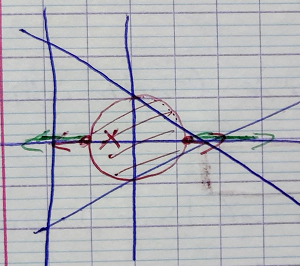
On a trouvé 2 minimum locaux sur $\mathbb R^2$ privé du disque $(0, 1)$. Le minimum global se trouve en (-1, 0)
Exemple 2
$$ x^2 + y^2 \leqslant 1 $$ $$ \Leftrightarrow $$ $$ c(x,y) = 1-x^2-y^2 $$ $$ c_2(-1/2, 0) = 3/4 \leqslant 0 $$donc le minimum global de $f(x,y)$ sur $\mathbb R^2$ vérifie la contrainte.
Les points qui rendent la contrainte $c_2(x, y) = 0$ active vérifient:
$$ \mathcal L(x, y, \lambda) $$avec
$$ \mathcal L_2(x, y, \lambda) = f(x, y) + \lambda (1-x^2-y^2) $$ $$ \Leftrightarrow $$ $$ \left \{ \begin{aligned} 4x + 2 - 2 \lambda x &= 0 \\ 2y + - 2 \lambda y &= 0 \\ 1 - x^2 - y^2 &= 0 \\ \end{aligned} \right . $$ $$ \left \{ \begin{aligned} x = 1, y = 0, \lambda = 3 \\ ou \\ x = 1, y = 0, \lambda = 1 \\ \end{aligned} \right . $$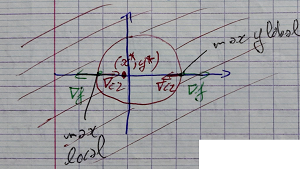
Prochaine article à venire: les notes de cours sur la résolution de systèmes linéaires (décomposition LU, itérations de Gauss-Seidel, Jacobi etc.)
No comments
 Donate
Donate