Convert implicit surface defined with global support to compact support

In mathematics functions are sometime characterized as compactly or globally supported. I will explain what it means and how to convert a function from global to compact support in the context of implicit surface modeling (i.e. boolean modeling with implicit surfaces as objects).
Compact Vs Global in 1D
What follows is not a strict definition but should give the intuition: a function with a compact support has its values vanishing to zero outside a specific range. For instance \( f : \mathbb R \rightarrow \mathbb R \) has a compact support if its values vanishes to zero as we go to \( -\infty \) or \( +\infty \):
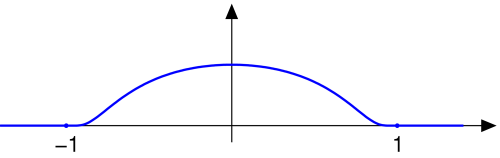
The function above is also called a bump function. We can bound the function variations in the interval \( [-1, 1] \) which is why we say \( f \) has a compact support.
A globally supported function is a function that never vanishes at infinity. For instance \( f(x) = x^2 \) has a global support.
Compact Vs Global in 3D for implicit surfaces
The following sections only deals with implicit surfaces (a.k.a distance fields) from a computer graphics perspective.
Example of compact support with Metaballs
Metaballs are defined with functions compactly supported. Indeed the scalar field is defined as the distance from the center of the Metaball with a function \( d : [0, +\infty] \rightarrow [1, 0]\) who usually looks like this:
$$ d( x) = \left (1 - min \left ( \frac{ x^2 }{ r_m^2 } , 1 \right ) \right )^4 $$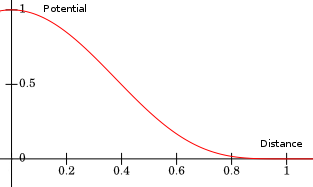
With \( r_m = 1\) for the radius of the Metaball. The surface of the Metaball is usually defined for every point \( \mathbf p \) such as \( d( \| \mathbf p - \mathbf c\|) = 0.5 \) with \( \mathbf c \) the center of the Metaball. The compact support of \( d \) enables us to define a 3D aligned bounding box of the scalar field. This box encloses all the none zero values of the Metaballs.
Here is a nice property: if we sum two Metaballs to blend them \( f(\mathbf x) = f_0(\mathbf x) + f_1(\mathbf x) \) we have the guarantee that the box of function \( f \) is equal to the union of the boxes of \( f_0 \) and \( f_1\). So we can roughly infer the region inside which a surface is present or not.
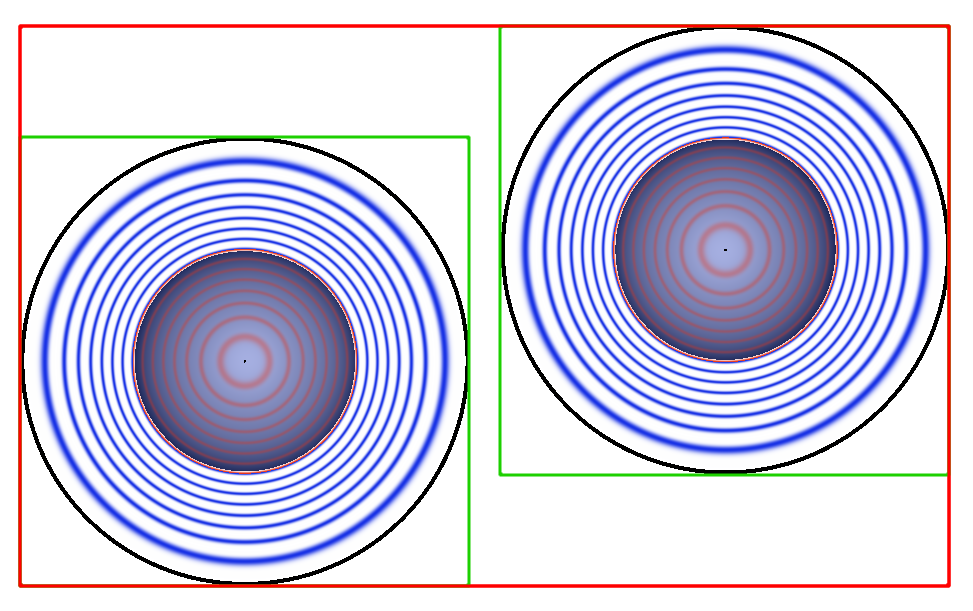
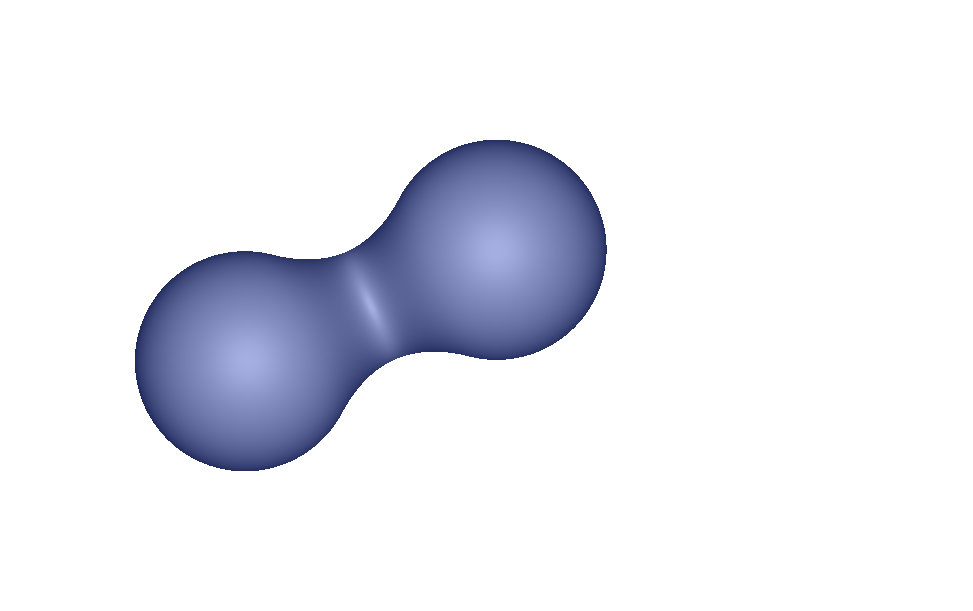
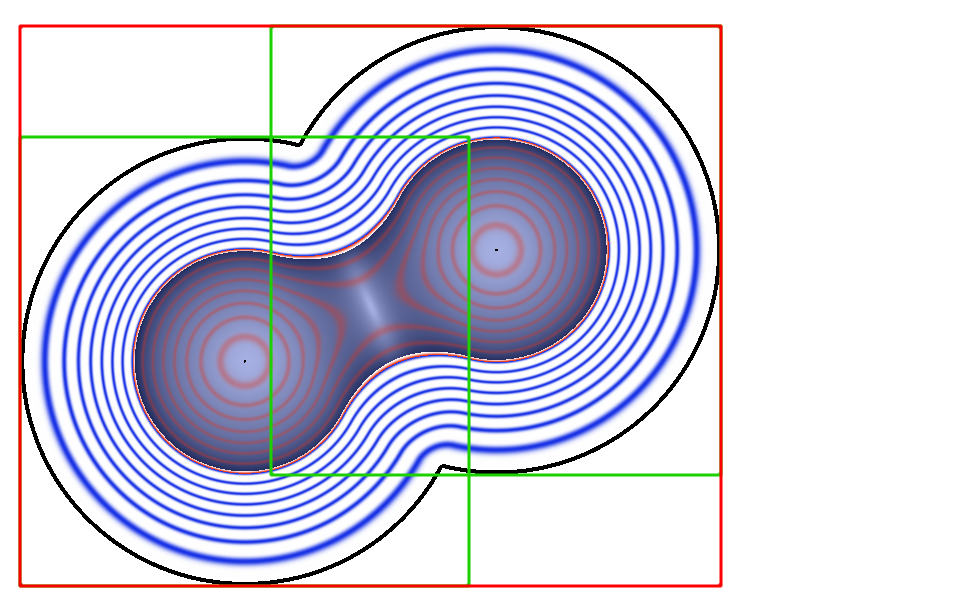
Above is an example of such blending. The figure on the right shows contour lines of the Metaballs as well as the associated axis aligned bounded boxes. The red box is the union of the green boxes for each Metaballs. Contour lines shows the variation of the potential. A red curves means \( f(\mathbf x) < 0.5 \) and blue \( f(\mathbf x) > 0.5 \). Black is used for very small values \( \epsilon << 10^{-3} \) and further away the potential is null.
Example of global support with the sphere equation
The function of a sphere of radius \( r_s \), depends on the distance from the center \( \mathbf c \) of the sphere to the evaluated point \( \mathbf x \) with:
$$ f(\mathbf x) = \| \mathbf x - \mathbf c \| - r_s = \sqrt{ (x-c_x)^2 + (y-c_y)^2 + (z-c_z)^2} - r_s $$
The surface is usually defined for every point \( \mathbf p \) such as \( f(\mathbf p) = 0 \). The support of \( f: [0, +\infty] \rightarrow [-r, +\infty] \) is global: the farther \( \mathbf x \) from \( \mathbf c \) is the bigger the value of \( f \). Its value never vanishes at \( +\infty \). As a consequence we cannot find a 3D bounded box to bound the values of \( f \). The function varies everywhere and may interact with other implicit objects anywhere.
Why compact support is better than global?
In the context of implicit surface modeling (modeling objects with booleans operators) compact support has two main advantages over global support.
Efficiency
Compact support can be faster if properly handled. The bounding box of the implicit surface can be used to create various data structures such as octrees or bounding box hierarchies to speed up the rendering. For instance when animating objects the marching cube algorithm can re-compute only what is inside the bounding box of an object to update triangles. The ray tracing of implicit surface will be of course a lot faster, the ray traversal through the scalar field can be accelerated by intersecting the hierarchy of boxes.
It is much harder to predict where the surface is with a globally supported scalar function. In this case bounding boxes have no obvious limits and the surface may be anywhere, especially if we use fancy blending operators between implicit surface primitives.
Composition
The famous '\( + \)' operator used to blend Metaballs cannot be used with global support functions. If we consider a sphere for instance the farther the other objects are from it the higher the potential of the sphere will be. This means that far away, objects will be altered more and more by the sphere's field. The object's surface defined by zero values will eventually disappear as we add the sphere's values. There is no way the sum produces the expected blend for globally supported functions unlike compact support.
There is actually two classes of composition operators (i.e blending, union, intersection etc.) one for global support and one for compact support. It is usually harder to create new composition operators for global support functions because it means we have to handle properly the whole ambient space. It is not rare that an operator behaves well at proximity of the implicit surface but introduces big distortion farther away in the scalar field. Later these "invisible" distortions can result in artifacts if other blends occurs.
Finally we can add that there is more interesting and controllable operators for compact support than global. For instance, "A Gradient-Based Implicit Blend" introduced by Olivier Gourmel & Al.
How to convert from global to compact using a map function
There is plenty of implicit surface primitives ranging from compact to global support. It would be a shame not to be able to use global support primitives. A simple solution is to use a function \(t_r : \mathbb R \rightarrow \mathbb R \) that maps the scalar field from a global to compact support. A globally supported primitive \( g : \mathbb R^3 \rightarrow \mathbb R\) can now be converted to a new compactly supported primitive \( f(\mathbf x) = t_r(g(\mathbf x)) \). Here is the definition and plot of \( t_r \):
$$ t_r(x)
=
\left\{
\begin{array}{ll}
1 & \mathrm{ if } \quad x < -r \\
0 & \mathrm{ if } \quad x > r \\
\frac{-3}{16} \left(\frac{x}{r}\right)^5 + \frac{5}{8} \left(\frac{x}{r}\right)^3 - \frac{15}{16} \left(\frac{x}{r}\right) + \frac{1}{2} & \mathrm{
otherwise }\mbox{ ,}\\
\end{array}
\right. $$
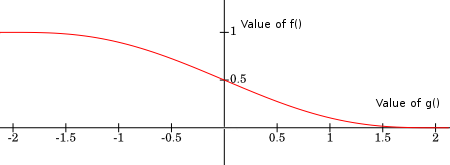
The plot of the function is done for \( r = 2 \). We can see that \( t_r \) correctly maps the values of \( g \) to the new values of \( f \) with compact support. When \( g(\mathbf x) = 0\) the composition returns \( t_r( g(\mathbf x) ) = 0.5 \) as the compact support convention requires. when we go away from the surface \( g > 0 \) and has increasing values which means \( t_r( g(\mathbf x) ) \) vanishes to zero if we reach the radius \( r \). On the contrary when we go inside \( g <0 \) and has diminishing values which means \( t_r( g(\mathbf x) ) \) will increase until we reach the radius \( r \).
Choose the radius \( r \) wisely. If \( r \) too small then the new surface defined by \( f \) will see its inner values set to a constant block of ones. This is a plot of a sphere function with global support converted to a compact support with different values of \( r \):

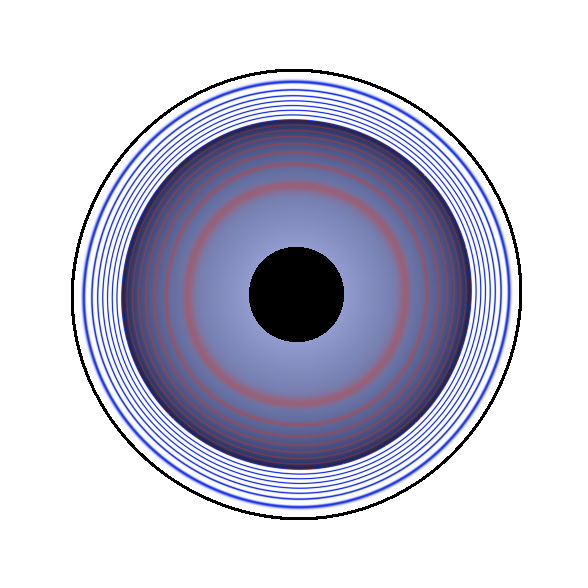
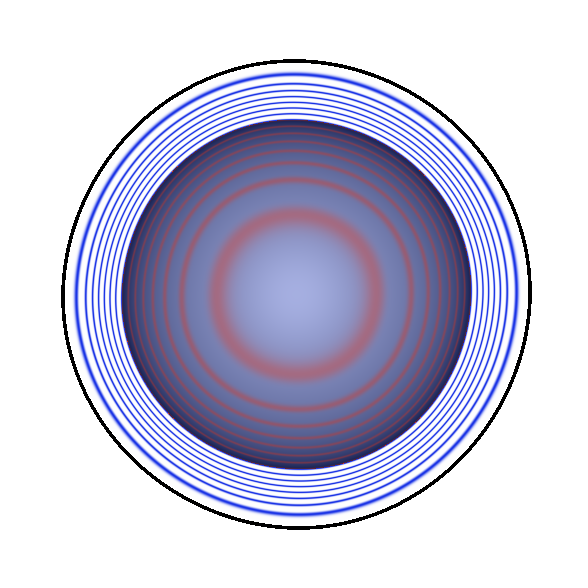
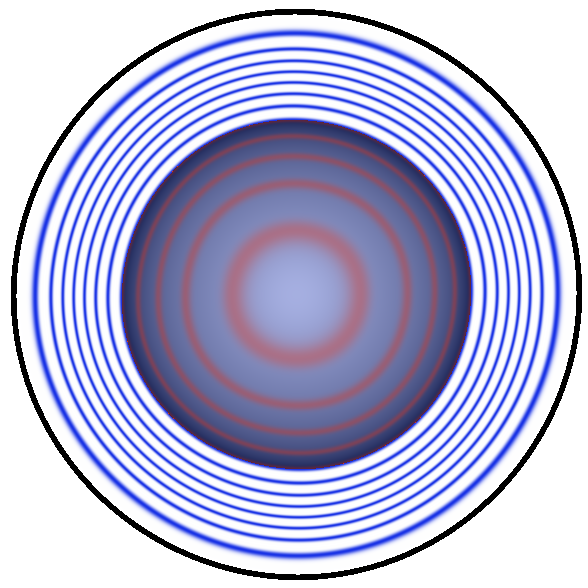
From left to right: the sphere, then the contour lines corresponding to the compact support from small to large radii \( r \) (not to be confused with the actual sphere radius). For smaller \( r \) we observe a black disc which corresponds to values equal to one. Inside the disc the gradient is null, in some application this can be problematic.
C++ code
/// @brief (-3/16)*(d/radius)^5 + (5/8)*(d/radius)^3 - (15/16)*(d/radius) + 1/2
/// junction is C2 at the boundary of the field [0, 1]
namespace to_compact {
float f(float dist, float radius) {
if(f < -radius)
return 1.f;
else if(f > radius)
return 0.f;
else {
// (-3/16)*(f/radius)^5+(5/8)*(f/radius)^3-(15/16)*(f/radius) + 1/2
const float fact = (f/radius);
const float fact2 = fact * fact;
const float fact4 = fact2 * fact2;
return (-3.f/16.f)*fact4*fact + (5.f/8.f)*fact2*fact - (15.f/16.f)*fact + 1.f/2.f;
}
}
void gf(float dist, float radius, Vec3& grad) {
if(f < -r || f > r)
grad = Vec3(0.f,0.f,0.f);
else {
// (-15/(16r))*(f/r)^4 + (15/(8*r))*(f/r)^2 - (15/(16r))
const float fact = f/r;
const float fact2 = fact*fact;
const float fact4 = fact2*fact2;
const float tmp = (-15.f/(16.f*r));
const float scale = tmp*fact4 + (15.f/(8.f*r))*fact2 + tmp;
grad = grad * scale;
}
}
float fngf(float dist, float radius, Vec3& grad) {
if(f < -radius) {
grad = Vec3(0.f,0.f,0.f);
return 1.f;
}
else if(f > radius) {
grad = Vec3(0.f,0.f,0.f);
return 0.f;
} else {
const float fact = (f/radius);
const float fact2 = fact * fact;
const float fact4 = fact2 * fact2;
// Compute grad
// (-15/(16r))*(f/r)^4 + (15/(8*r))*(f/r)^2 - (15/(16r))
const float tmp = (-15.f/(16.f*radius));
const float scale = tmp*fact4 + (15.f/(8.f*radius))*fact2 + tmp;
grad = grad * scale;
// Compute potential
// (-3/16)*(f/radius)^5+(5/8)*(f/radius)^3-(15/16)*(f/radius) + 1/2
return (-3.f/16.f)*fact4*fact + (5.f/8.f)*fact2*fact - (15.f/16.f)*fact + 0.5f;
}
}
}
No comments
 Donate
Donate