C++ code for cotangent weights over a triangular mesh

Here is some code to compute the cotangent weights described in the article:
"Discrete Differential-Geometry Operators for Triangulated 2-Manifolds"
Motivation
In numerous application you need to apply the so called "discreete Laplacian operator" \( \Delta\) to a function defined over the surface of some mesh. The most popular way to apply the Laplace operator on a triangle mesh is to compute the "Cotangent weights" (or cotan weights). The Laplacian, and its discrete definition on a mesh through cotangent weights, has many application:
- Mesh smoothing.
- Computing harmonic weights over a mesh.
- Diffusing values over its surface.
- and much more...
Definition
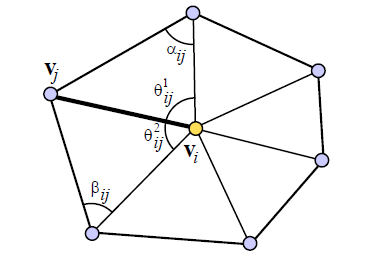
A cotangent weight can be thought as barycentric weights, for every vertex \( i \) we associate a weight \( w_{ij} \) to each of its direct neighbor \( j \).
$$w_{ij} = \cot(\alpha_{ij}) + \cot(\beta_{ij})$$
The code below does not compile but hopefully it can serve as a reference to adapt it to your own project. It also handles cotangent weights at the boundaries of the mesh.
struct Mesh {
/// For every vertex, a list of direct (1st ring) neighbors.
/// first_ring[index_vertex].size() == number of direct neighbors to 'index_vertex'
/// first_ring[index_vertex][ith_neighbor] == neighbor_index
std::vector< std::vector<Vert_idx> > first_ring();
Vec3 vertex(Vert_idx idx) const { return _vertices[idx]; }
int nb_vertices() const { return (int)_vertices.size(); }
std::vector<Vec3> _vertices;
};
// -----------------------------------------------------------------------------
void laplacian_cotan_weights(const Mesh& m,
std::vector< std::vector >& per_edge_cotan_weights)
{
int nb_verts = m.geom().nb_vertices();
per_edge_cotan_weights.resize( nb_verts );
for(int vertex_i = 0; vertex_i < nb_verts; ++vertex_i)
{
const int nb_neighs = (int)m.first_ring()[vertex_i].size();
per_edge_cotan_weights[vertex_i].resize( nb_neighs );
for(int edge_j = 0; edge_j < nb_neighs; ++edge_j)
{
float wij = laplacian_positive_cotan_weight(m, vertex_i, edge_j);
per_edge_cotan_weights[vertex_i][edge_j] = wij;
}
}
}
// -----------------------------------------------------------------------------
float cotan(const Vec3& a, const Vec3& b){
return a.dot(b)) / (a.cross(b)).norm();
}
// -----------------------------------------------------------------------------
/// compute the cotangent weight for the edge (v_i, v_j)
float laplacian_cotan_weight(const Mesh& m,
Vert_idx vertex_i,
int edge_j )
{
int nb_neighs = (int)m.first_ring()[vertex_i].size();
Vert_idx vertex_j = m.first_ring()[vertex_i][ edge_j ];
Vert_idx vertex_j_next = m.first_ring()[vertex_i][ (edge_j+1) % nb_neighs ];
Vert_idx vertex_j_prev = m.first_ring()[vertex_i][ (edge_j-1) >= 0 ? (edge_j-1) : nb_neighs-1 ];
Vec3 v1 = m.vertex(vertex_i) - m.vertex(vertex_j_prev);
Vec3 v2 = m.vertex(vertex_j) - m.vertex(vertex_j_prev);
Vec3 v3 = m.vertex(vertex_i) - m.vertex(vertex_j_next);
Vec3 v4 = m.vertex(vertex_j) - m.vertex(vertex_j_next);
float cotan_alpha = cotan(v1, v2);
float cotan_beta = cotan(v3, v4);
// If the mesh is not a water-tight closed volume
// we must check for edges lying on the sides of wholes
if(m.is_vert_on_side(vertex_i) && m.is_vert_on_side(vertex_j))
{
// boundary edge, only have one such angle
if( vertex_j_next == vertex_j_prev )
{
// two angles are the same, e.g. corner of a square
cotan_beta = 0.0f;
// Note this case should be avoided by flipping the edge of the
// triangle...
}
else
{
// find the angle not on the boundary
if( m.is_vert_on_side(vertex_i) && m.is_vert_on_side(vertex_j_next) )
cotan_beta = 0.0;
else
cotan_alpha = 0.0f;
}
}
float wij = (cotan_alpha + cotan_beta)/* / 2.0f*/;
if( isnan(wij) ){
wij = 0.0f;
}
// compute the cotangent value close to 0.0f and pi.
// as cotan approaches infinity close to those values
// we clamp.
const float eps = 1e-6f;
const float cotan_max = cos( eps ) / sin( eps );
wij = clampf(wij, -cotan_max, cotan_max);
return wij;
}
Note: recall that \( \cot( \theta ) = \frac{\cos \theta}{\sin \theta} =\frac{\vec u . \vec v}{ \|\vec u \times \vec v\|} = \frac{\|\vec u\|.\|\vec v\| cos(\theta) }{\|\vec u\|.\|\vec v\| sin(\theta)} \)
Negative weights
Sometimes cotangent weights can be negative and causes instabilities for certain configurations of triangles depending on your algorithm. For instance, a gradient descent that won't converge correctly.
Here is an alternate implementation of the cotangent weights where the absolute value of \( cos(\alpha) \) and \( sin(\beta) \) which results in positive cotangent weights, this kind of hacky use at your own risks:
float laplacian_positive_cotan_weight(const Mesh& m,
Vert_idx vertex_i,
int edge_j )
{
const int nb_neighs = (int)m.first_ring()[vertex_i].size();
Vert_idx vertex_j = m.first_ring()[vertex_i][ edge_j ];
Vert_idx vertex_j_next = m.first_ring()[vertex_i][ (edge_j+1) % nb_neighs ];
Vert_idx vertex_j_prev = m.first_ring()[vertex_i][ (edge_j-1) >= 0 ? (edge_j-1) : nb_neighs-1 ];
Vec3 pi = m.vertex(vertex_i);
Vec3 pj = m.vertex(vertex_j);
Vec3 pj_prev = m.vertex(vertex_j_prev);
Vec3 pj_next = m.vertex(vertex_j_next);
float e1 = (pi - pj ).norm();
float e2 = (pi - pj_prev).norm();
float e3 = (pj_prev - pj ).norm();
// NOTE: cos(alpha) = (a^2.b^2 - c^2) / (2.a.b)
// with a, b, c the lengths of of the sides of the triangle and (a, b)
// forming the angle alpha.
float cos_alpha = fabs((e3*e3 + e2*e2 - e1*e1) / (2.0f*e3*e2));
float e4 = (pi - pj_next).norm();
float e5 = (pj_next - pj ).norm();
float cos_beta = fabs((e4*e4 + e5*e5 - e1*e1) / (2.0f*e4*e5));
// NOTE: cot(x) = cos(x)/sin(x)
// and recall cos(x)^2 + sin(x)^2 = 1
// then sin(x) = sqrt(1-cos(x))
float cotan1 = cos_alpha / sqrt(1.0f - cos_alpha * cos_alpha);
float cotan2 = cos_beta / sqrt(1.0f - cos_beta * cos_beta );
// If the mesh is not a water-tight closed volume
// we must check for edges lying on the sides of wholes
if(m.is_vert_on_side(vertex_i) && m.is_vert_on_side(vertex_j))
{
if( vertex_j_next == vertex_j_prev )
{
cotan2 = 0.0f;
} else {
if( m.is_vert_on_side(vertex_i) && m.is_vert_on_side(vertex_j_next) )
cotan2 = 0.0;
else
cotan1 = 0.0f;
}
}
// wij = (cot(alpha) + cot(beta))
float wij = (cotan1 + cotan2) / 2.0f;
if( isnan(wij) ){
wij = 0.0f;
}
// compute the cotangent value close to 0.0f.
// as cotan approaches infinity close to zero we clamp
// higher values
const float eps = 1e-6f;
const float cotan_max = cos( eps ) / sin( eps );
if(wij >= cotan_max ){
wij = cotan_max;
}
return wij;
}
References
Some research paper making use of cotangent weights:
- Automatic Rigging and Animation of 3D Characters
(especially the section computing skinning weights)
Limitations and beyond cotan weights
The above weights will only work on "clean triangle meshes", which means you don't want self-intersections, separate islands of vertices, holes etc. Cotangent weights are good for manifold meshes only:



Intrinsic meshes
Fortunately there are more robust ways to compute the Laplacian on triangle meshes, for instance the authors of the paper Laplacian for Non-manifold Triangle Meshes also provide source code to compute a better Laplacian matrix that you can just replace with the one you build with cotangent weights! With this new Laplacian you can handle mesh like:




- To understand the technique see my transcript of their siggraph presentation video.
- Standalone application.
- Geometry Central is a geometry processing library that provides it as well.
This particular work is the development of another research about "Intrinsic meshes". Any standard triangle mesh can be converted to this new "Intrinsic mesh" representation which is easier to work with in many situations (for instance to compute Partial Differential Equations). See my transcript about their presentation on Intrinsic meshes.
Bonus: polygonal meshes
So far, we only discussed methods to compute the Laplacian on triangle meshes, but what about quads or other polygons? You should probably have a look to: Discrete Differential Operators on Polygonal Meshes by Fernando de Goes & Al.
One comment
 Donate
Donate
this is cool
yes - 16/04/2018 -- 21:18